We’re not as 3-Dimensional as We Think

silentbob4 Aug 2024 14:39 UTC
36 points
16 comments5 min readLW link

While thinking about high-dimensional spaces and their less intuitive properties, I came to the realization that even three spatial dimensions possess the potential to overwhelm our basic human intuitions. This post is an exploration of the gap between actual 3D space, and our human capabilities to fathom it. I come to the conclusion that this gap is actually quite large, and we, or at least most of us, are not well equipped to perceive or even imagine “true 3D”.

What do I mean by “true 3D”? The most straightforward example would be some ℝ³ → ℝ function, such as the density of a cloud, or the full (physical) inner structure of a human brain (which too would be a ℝ³ → whatever function). The closest example I’ve found is this visualization of a ℝ³ → ℝ³ function (jump to 1:14):

(It is of course a bit ironic to watch a video of that 3D display on a 2D screen, but I think it gets the point across.)

Vision

It is true that having two eyes allows us to have depth perception. It is not true that having two eyes allows us to “see in 3D”. If we ignore colors for simplicity and assume we all saw only in grayscale, then seeing with one eye is something like ℝ² → ℝ as far as our internal information processing is concerned – we get one grayscale value for each point on the perspective projection from the 3D physical world onto our 2D retina. Seeing with two eyes then is ℝ² → ℝ² (same as before, but we get one extra piece of information for each point of the projection, namely depth[1]), but it’s definitely not ℝ³ → (...). So the information we receive still has only two spatial dimensions, just with a bit more information attached.

Also note that people who lost an eye, or for other reasons don’t have depth perception, are not all that limited in their capabilities. In fact, other people may barely notice there’s anything unusual about them. The difference between “seeing in 2D” and “seeing with depth perception” is much smaller than the difference to not seeing at all, which arguably hints at the fact that seeing with depth perception is suspiciously close to pure 2D vision.

Screens

For decades now, humans have surrounded themselves with screens, whether it’s TVs, computer screens, phones or any other kind of display. The vast majority of screens are two-dimensional. You may have noticed that, for most matters and purposes, this is not much of a limitation. Video games work well on 2D screens. Movies work well on 2D screens. Math lectures work well on 2D screens. Even renderings of 3D objects, such as cubes and spheres and cylinders and such, work well in 2D. This is because 99.9% of the things we as humans interact with don’t actually require the true power of three dimensions.

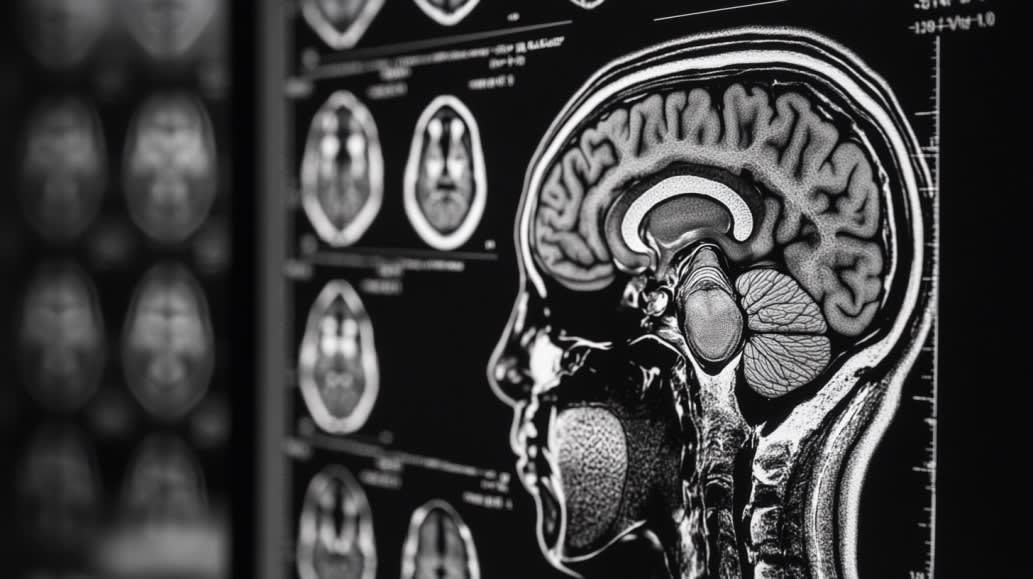
There are some exceptions, such as brain scans – what is done there usually is to use time as a substitute for the third dimension, and show an animated slice through the brain. In principle it may be better to view brain scans with some ~holographic 3D display, but even then, the fact remains that our vision apparatus is not capable of perceiving 3D in its entirety, but only the projection onto our retinas, which even makes true 3D displays less useful than they theoretically could be.

Brain scans are one of the relatively few examples where humanity is confronted with “true 3D”. The standard solution here is to visualize 2D slices, and use time as a substitute for the third dimension, by varying which slice is being displayed.

Video Games

The vast majority of 3D video games are based on polygons: 2D surfaces placed in 3D space. Practically every 3D object in almost any video game is hollow. They’re just an elaborate surface folded and oriented in space. You can see this when the camera clips into some rock, or car, or even player character: they’re nothing but a hull. As 3D as the game looks, it’s all a bit of an illusion, as the real geometry in video games is almost completely two-dimensional.

Here’s one example of camera clipping:

The only common exception I’m aware of is volumetric smoke – but this is primarily a visual gimmick.

You might now say that there’s something I’m overlooking, namely voxel games, such as Minecraft or Teardown. Voxel engines are inherently 3-dimensional! But even then, while this is true, Minecraft is in its standard form still using 2D polygons to render its voxels.

Some video games render proper volumetric smoke, in the sense of actually visualizing something like a ℝ³ → ℝ function. However, it’s still common to rely on polygon based smoke rendering, which achieves good enough visual results in the majority of cases.

Volumes

Stop reading for a second and try to imagine a mountain in as much detail as possible.

The mountain in your head may at first glance seem quite 3-dimensional. But when you think of a mountain, you most likely think primarily of the surface of a mountain. Sure, you are aware there’s a bunch of matter below the surface, but is the nature of that matter below the surface truly an active part of your imagination while you’re picturing a mountain? In contrast, imagine a function from ℝ³ → ℝ. Something like a volumetric cloud with different densities at each point in 3D space. We can kind of imagine this in principle, but I think it becomes apparent quickly that our hardware is not as well equipped for this, particularly once the structures become more detailed than the smooth blobbyness of a cloud. And even if you’re able to think about complex volumes, it becomes much more difficult once you try to discuss them with others, let alone create some accurate visualization that preserves all information.

Let’s forget about mountains and clouds, and do something as seemingly simple as visualizing the inner complexity of an orange. Can you truly do that? In high detail? Do you really have an idea what shape an orange would have from the inside, in 3D? Where are the seeds placed? What do the orange’s cells look like in 3D and how are they arranged? How and where are the individual pieces separated by skin, and so on?

Most people are just fine picturing a slice of an orange, or an orange cut in half – but that would once again reduce it to surfaces. Imagining an orange in true 3D is difficult, no less because we simply have never actually seen one (and wouldn’t really be able to, because, once again, we can’t truly see in 3D, but only 2D projections with depth perception).

What the mountain in my head roughly looked like. In my case I notice this is even closer to the truth than first expected – my imagination, it turns out, most of the time is actually 2D, as if I was “imagining on a screen”. It takes some extra conscious effort to imagine things with depth. So imagining the surface of a mountain “3D style” is possible, but it’s still mostly the surface shape that my mental compute is spent on, whereas any volumetric happenings below the surface are hard to fathom. I wonder if others have a similar experience.

Volume

For most people it’s rather unintuitive how similar in size a sphere of double the volume of another sphere looks. Maybe you know on System 2 level that the third root of 2 is about 1.26, and hence a ball of radius 1.26 would have double the volume of a ball of radius 1. Still, if you put these two balls in front of random people and let them estimate the ratio of the volumes, the average answer you’ll get will very likely be much smaller than 2.

I admittedly thought this image would look more impressive. See footnote [3] for the volume ratio of these two spheres. I suggest making a quick intuitive prediction beforehand.

Habitat

Lastly, an evolutionary reason for why it makes sense that our brains don’t truly grasp three dimensions: for most of history, humans cared most about surfaces and very little about volumes. We live on the ground. Most of the things we meaningfully interact with are solid, and hence the shared interface is their and our surface.

There are some animals that live in true 3D. Most notably fish. Birds? Probably much more than us, but birds are already pretty surface-bound for much of their lives. Theoretically animals that dig tunnels might also benefit from proper 3D processing capabilities, but most of them are small and probably don’t have the mental complexity required to really grasp three dimensions. What about apes? Well, anything that’s climbing a lot certainly has more need for verticality than us, but still, I’d argue it’s very similar in nature to what humans are up to, when it comes to spatial perception. It’s all about surfaces, and very often even about 1-dimensional properties such as the distance between some prey or predator and yourself. Your brain is trained to care about distances. It’s less well equipped to think about areas. Even less to think about complex volumes.

Conclusion

We tend to think of ourselves as “3D natives”, but it turns out that 3D can go quite far beyond what our brains are good at processing. “True” 3D geometry can quickly overwhelm us, and it’s easy to underestimate what it actually entails. Whether this realization is useful or not, I certainly find it interesting to think about. And if you have indeed read this whole post up to this point, then I hope you do too[2].

  1. ^

    Depth of course is not what we get directly, but the interpretation our brain ends up with based on the two input channels that are our two eyes; but what ends up in our awareness then is not two separate images from the eyes, but instead this mix of brightness (or color) and depth.

  2. ^

    I suspect some readers will rather disagree with the post and (probably rightly) insist that they are indeed able to intuitively think about complex 3D structures without major issues. I certainly don’t think it’s impossible to do so. But I still think that there’s quite a gap between “the kind of 3D we need to deal with to get through life”, and “the full extent of what 3D actually means”, and that it’s easy to overlook that difference.

  3. ^

    The larger sphere has roughly 2.3x the volume of the smaller sphere (hard to say exactly, as the spheres are in fact not perfectly spherical)

silentbob4 Aug 2024 14:39 UTC
36 points
16 comments5 min readLW link