Learning as you play: anthropic shadow in deadly games
Epistemic status: I’m not a mathematician, but this is simple stuff and I think I double checked all my calculations well enough. Criticism is welcome!
Some time ago a post came out claiming that “anthropic shadow is reflectively inconsistent”. I want to argue the exact opposite thesis: anthropic shadow is a trivially true phenomenon, and it is in fact just a special case of a phenomenon that applies to a wide class of possible games, and is fundamentally unavoidable.
To put forward a formal thesis:
Given a game that possesses the following characteristics:
there is some aspect of the rules that is unknown to the player, and can not be deduced by observing other games (either because there are no other games, or because the rules are fully randomized every time);
said unknown aspect of the rules affects in some way the player’s ability to gather information about the game by playing, e.g. by abruptly ending it, or by obfuscating outcomes;
then the average player will not be able to play optimally based only on in-game observations.
It is pretty trivial stuff if one thinks about it; obviously, if the unknown rules mess with our ability to learn them, that reflective quality fundamentally rigs the game. The most obvious example of this are what I’ll call “deadly games”—namely, games in which one outcome abruptly ends the game and thus makes all your accumulated experience useless. This property of such games however is fundamental to their self-reflexive nature, and it has nothing to do with death per se. If instead of dying you are kicked out of the game, the result is the same. “Anthropic undeath” doesn’t fix this: the fundamental problem is that you start the game ignorant of some crucial information that you need to play the game optimally, and you can’t learn that information by playing because any event that would give you valuable bits to update your beliefs reflexively messes with your ability to observe it. Therefore, your sampling of a game trajectory from inside a game will always be incomplete, and if information can’t be carried from one game to another, this will be a chronic, unfixable problem. You can’t play at your best because the deck is stacked, you don’t know how, and the dealer reshuffles new cards in every time.
A game of Chinese Roulette
Let’s come up with a game that we’ll call Chinese Roulette. This game is a less hardcore version of Russian Roulette; you have a six chamber revolver, of which an unknown number of chambers are loaded. At every turn, the drum is spun and you have to fire a round; the name of the game comes from the fact that you don’t point the gun at your own head, but at an antique Chinese vase of value . Every time you pull the trigger and the chamber is empty you get a reward ; if you do fire a bullet though, the vase is irreparably destroyed and the game ends. At any point before you can choose however to quit the game and get the vase as a consolation prize.
The optimal strategy for the game is simple enough. Individual rounds are entirely uncorrelated (remember, the drum is spun again before every round), so the only strategies that make sense are “keep firing for as long as possible” or “quit immediately”. If you keep firing, your expected winnings are:
If you quit, instead, you immediately get . In other words, playing is only advantageous if
Knowing the actual amount of bullets in the gun, , is essential to know the correct strategy; without that information, we are always at risk of playing sub-optimally. If we start with a full ignorance distribution and thus assume that could take any allowed value with equal likelihood, our average expectation will be , and thus we should never play if . But suppose that instead is high enough that we do choose to play—do we ever get a chance, by playing, to get a more accurate guess at and if necessary correct our mistake? As it turns out, no.
The Bayesian approach to this is obviously to form a prior belief distribution on the possible values of and then update it, as we play, with each observed sequence of outcomes to find our posterior:
Unfortunately, if we label the possible outcomes of each pull of the trigger with either (for Empty) or (for Loaded, resulting in a shot and the vase being destroyed), the only possible sequences we can observe while still playing are , , … you get the drift. There’s no chance to see anything else; if we did, the game would be over. And if at, say, the fifth turn, there is no alternative to seeing , that means that the probability of observing it, conditioned on us still being in play, is , and entirely independent of . No information can be derived to update our prior. Whatever our ignorance at the beginning of the game, it will never change—until it’s too late for it to be of any use. This is essentially the same as any typical anthropic shadow situation; we either never observe failure, or we observe it but have no way of leveraging that information to our benefit any more. While inside the game it’s impossible to gain information about the game; when outside the game, any information we gained is useless. Based on the values of the rewards:
if , we can be sure that quitting is optimal;
if , we can be sure that playing is optimal;
for , our strategy will depend entirely on our prior, and if it’s wrong, there’s no way to correct it.
This frustrating situation is the purest form of anthropic shadow. But there are games in which things aren’t quite so black and white.
The only winning move is not to play—sometimes
Let’s play a more interesting version of Chinese Roulette. In this, we fix the amount of bullets in the revolver to , so that there’s a 50% of finding a loaded chamber at every turn. Bullets are replaced every turn, and they’re drawn from a bag which contains an unknown fraction of blanks. So when we fire there are in general three possible outcomes:
there’s a probability of that the chamber is empty, and we get our reward ;
there’s a probability of that the gun fires a blank; we don’t get a reward, but the game continues;
there’s a probability of that the gun fires a real bullet. In that case, the game ends.
We can call the fraction of real bullets . Obviously, . Then the reward for playing is
Which means that playing is advantageous if
Makes sense: the more blanks there are, the safer the game is, and the higher the value of the vase would have to be to justify quitting. The player can then try to form a belief on the value of , updating it as the game goes, and decide turn by turn whether to continue playing or quit while still ahead. We still assume total ignorance, so at the start,
Since the outcome of a non-blank loaded chamber is unobservable, there are two possible events we can observe:
an empty chamber , with probability ;
a loaded chamber with a blank, with probability .
Then the probability of a given sequence with loaded chamber events and total turns is
We can thus calculate our posterior by performing an integral:
calculated by using
in which we’ve made use of , Gauss’ hypergeometric function (by the way, check them out—hypergeometric functions are fun! - at least if you’re the kind of nerd that thinks words like “hypergeometric function” and “fun” can belong in the same sentence, like I am). So the posterior is:
And it doesn’t take much to figure out that the expectation value for is
To see how that function evolves, here is an example of a few paths:
Notice how sequences in which few or no loaded chambers are observed quickly converge to a very low guess on , and vice versa; seeing very few loaded chambers with blanks (near misses) while still in play is bad news, because it suggests we’re playing under anthropic shadow, and most loaded chambers have real bullets. Seeing an almost perfect 1:1 ratio between loaded and empty chambers however is reassuring, and suggests that maybe there’s no real bullets at all.
Working out exact formulas for the statistics of this game is hard, but fortunately it’s not too difficult to treat it numerically in polynomial time. The game can be described as a Markov process; after turns, each player will be in one of the states spanned by
The transition rules are semi-probabilistic, but can be easily split in two stages. The first stage of a turn is the trigger pull:
with (empty chamber)
with (loaded chamber, blank)
with (loaded chamber, real bullet)
Then the still playing players go through an additional step:
if their expected reward for playing, ,
One can then keep an appropriate tally of probabilities and rewards for each state, and grow the array of states as turns pass—until the total sum of players still in play falls below a certain threshold and we can declare the game solved. Using this method, I’ve produced this map of average relative rewards (average reward divided by the optimal reward for the given combination of and ) for different games.
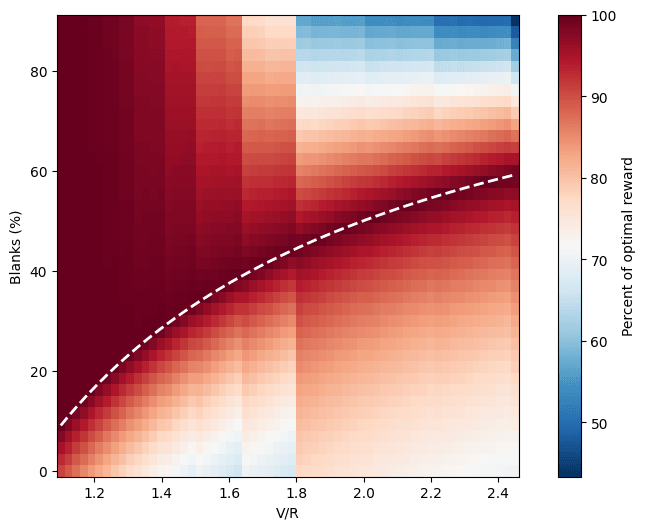
The map shows very well the anthropic shadow effect. The white dashed line marks , the border between the region in which quitting is optimal (below) and the one in which playing is (above). Low values of make quitting not worth much, and encourage playing; thus the area above is very dark red, but the one below veers towards blue. This is the region in which people keep playing despite the game being very unfair (low or zero percentage of blanks); it is the most typical example of anthropic shadow. Most players are eliminated quickly; the ones that keep going are unable to learn enough to realize how badly the odds are stacked against them before their luck runs out. In the end, almost no one gets to do the wise thing, and quit while they’re ahead.
The same problem in reverse happens in the top right corner. Here the consolation prize is high, and quitting is tempting; it takes only a slightly unlucky streak to decide to go for it. However, this is an area in which the game is very lenient, and ultimately, it might be worth to keep going for a while longer instead, so players lose out of excessive prudence. If instead of a precious vase it was their life on the line, though, at least they’d get to keep their head!
One thing that jumps to the eye is the “banded” look of the graph. There’s a particularly sharp transition around . I initially thought this might be a bug, but turns out it’s a natural feature of the system. Its origin is clear enough if we look at the map of how many players quit:
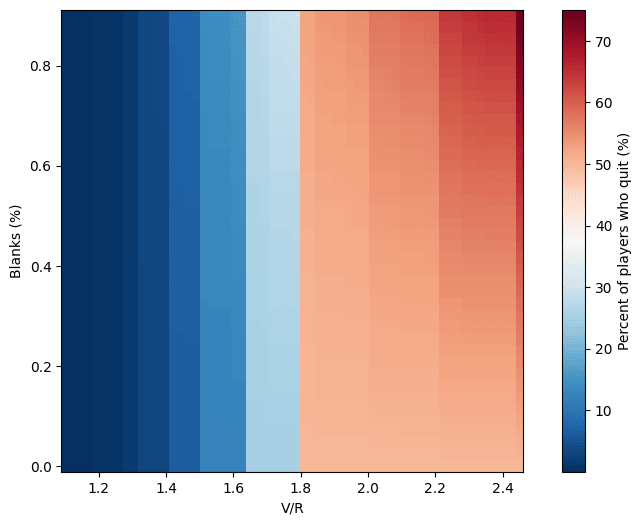
The banded structure is even more evident here. The reason for it is simple: updates on beliefs are performed discreetly, at each turn. There are only a discrete amount of possible values that the expectation can take, and especially at the beginning, when and are small, the value can swing wildly in a single turn. The bands reflect points at which such a likely early swing involving large fractions of the players’ population crosses the boundary between playing and quitting. As it turns out, for , all the players who get an empty chamber quit after the very first turn!
A matter of viewpoints
As I was working on this post though I suddenly realized something. I made my players use the strategy of estimating , and then using it to predict their expected winnings, so that they quit if:
But wait, someone might say! Wouldn’t the correct way to do this be to estimate directly your expected winnings? So essentially:
Well, it’s not so simple.
Mathematically, the integral above is a pain; it doesn’t converge. This is because as , ; if there’s no chance of breaking the vase, you can keep playing and winning forever. It’s also not solvable in closed form, that I can tell. This could be obviated by putting an upper limit (lower than , but very close) on , and then integrating numerically. It’s annoying, it probably will make the computation longer and slightly less precise, but it’s doable.
Tinkering a bit with it, I realized that (unsurprisingly, given its going-to-infinity tendencies) estimating the reward in this way always tends to give higher values than the method I’ve used. This means it leads to a policy that incentivizes risk, and playing, over quitting[1]. Qualitatively, I expect it to result in that map from the previous section getting a lot more blue below the white line and a lot more red above it.
And then it hit me that this isn’t just a mathematical conundrum—it’s a philosophical one. One kind of player tries to assess the probability of the events independently of how beneficial they are, and only later calculate (conservatively) how much they can get out of them. The other immediately weighs the expected benefits, to the point that the tiniest sliver of chance of near-infinite winnings overshadows everything else and incentivizes playing. Why, I can’t think of any debate surrounding potentially existential risks going on right now that this sort of dichotomy applies to. Can you?
Conclusions
I’ve tried to demystify the concept of anthropic shadow, separating it from actual discussions of life and death. The anthropic shadow effect is just an example of a common artifact in a certain type of games; ones in which we don’t know all the rules, and discovering them through play is hindered by the fact that different outcomes affect the length of the game. In these conditions, depending on the nature of the game, we’re pretty much doomed to play sub-optimally.
There are a few ways to escape or at least defend ourselves from the trap. Knowledge that allows at least partial leveraging of the information that we possess is possible, granted that we know some of the probabilities involved in the game in absolute terms. Having a better-than-complete-ignorance prior helps too. In both cases, we need information from a different source than playing the game, some knowledge to ground ourselves. Simple statistical observation won’t cut it; we need mechanistic knowledge to predict at least some information from first principles, so that it’ll be independent from the phenomenon that hides some outcomes from our view.
This doesn’t solve our problems. But now you know. And knowing, it turns out, is an as-of-yet unspecified fraction of the battle.
- ^
Actually, this only happens if the limit for is very close to 1; if , for example, then it’s another story. But that’s a completely different game too.
This doesn’t make sense to me. Why am I not allowed to update on still being in the game?
I noticed that in your problem setup you deliberately removed n=6 from being in the prior distribution. That feels like cheating to me—it seems like a perfectly valid hypothesis.
After seeing the first chamber come up empty, that should definitively update me away from n=6. Why can’t I update away from n=5 ?
Yes, the n=6 case is special. I didn’t mean to “cheat” but I simply excluded it because it’s trivial. But past the certainty that the game isn’t rigged that much, you can’t gain anything else. If you didn’t condition on the probability of observing the sequence, nothing would actually change anyway. Your probability distribution would be
P(n)∝(1−n6)N(properly normalized, of course). This skews the distribution ever further towards low values of n, irrespective of any information about the actual gun. In other words, if you didn’t quit at the beginning, this will never make you quit—you will think you’re safer and safer by sheer virtue of playing longer, irrespective of whether you actually are. So, what use are you getting out of this information? None at all. If you are in a game that is worth playing, you gain zero; you would have played anyway. If you are not in a game that is worth playing, you lose in expectation the difference V−WPLAY. So either way, this information is worthless. The only information that is useful is one that behaves differently (again, in expectation) between a world in which the optimal strategy is to play, and one in which the optimal strategy is to quit, and allows you to make better decisions. But there is no such useful information you can gain in this game upstream of your decision.
Also please notice that in the second game, the one with the blanks, my criterion allows you to define a distribution of belief that actually you can get some use out of. But if we consistently applied your suggested criterion, and did not normalize over observable paths, then the belief after E empty chambers would just be
P(b;E)=(E+1)bEwhich behaves exactly like the function above. It’s not really affected by your actual trajectory, it will simply convince you that playing is safer every time an empty chamber comes up, and can’t change your optimal strategy. Which means, again, you can’t get any usefulness out of it. This for an example of a game in which instead using the other approach can yield some gains.
This post seems incorrect to me. Here’s the crux:
Well yes, conditioned on us being in play, we can’t get any more information from the sequence of events we observed. But the fact that we are still in play itself tells us that the gun is mostly empty. Now as it happens this isn’t very useful because we will never both update towards not playing, and be able to carry on playing, but I can still be practically certain after seeing 20 Es in a row that the gun is empty.
The way anthropics twists things is that if this were russian roulette I might not be able to update after 20 Es that the gun is empty, since in all the world’s where I died there’s noone to observe what happened, so of course I find myself in the one world where by pure chance I survived.
No, it tells us that either the gun is mostly empty, or we were very lucky; but since either way that cancels out exactly with our probability of being still in play in the first place, no additional information can be deduced with which to decide our strategy. The bit about this being conditioned on being still in play is key! If we consider the usefulness of each bit of information acquired, then obviously they can only be useful if you’re still playing.
Why are we conditioning on still being in play though? Without the anthropic shadow there’s no reason to do so. There are plenty of world’s where I observe myself out of play, but with different information, why is the fact I’m not in one of them not telling me anything?
To give a concrete counterexample.
Let’s say each round there’s a 50 percent probability of adding an extra bullet to the gun.
If I didn’t update based on the fact I’m still playing then I would quickly stop after a few rounds, since the probability I would see a bullet constantly increases.
But if I do update, then it’s worth it carrying on, since the fact I’m still playing is evidence there still are plenty of empty chambers.
There are! But here I am only interested in useful information, bits of information you can use to update your strategy. In those worlds you just acquired bits of information that have zero usefulness. While information would still be useful, though, you won’t acquire it. I should probably try to formalise this concept more, and I will maybe write something else about it.
See my comment from earlier below, which highlights how this information is in general useful, even if in this case it happens not to be:
Not quite getting it—is the addition permanent or just for each round? Seems to me like all that does is make the odds even worse. If you’re already in a game in which you should quit, that only is all the more reason; if you’re not, it could tilt the scales. And in neither case does updating on the fact you’re still playing help in any way, because in fact you can’t meaningfully update on that at all.
The addition is permanent. Updating on the fact that you’re still playing provides evidence that the bullet was not in fact added in previous rounds, so it’s worth carrying on playing a little bit longer, whereas if you didn’t update, even if it was worth playing the first round, you would stop after 1 or 2.
OK, so if you get told that a bullet was added, then yes, that is information you can use, combined with the knowledge that the drum only holds maximum 6 bullets. But that’s a different game, closer to the second I described (well, it’s very different, but it has in common the fact that you do get extra information to ground your beliefs).
Even simpler, something similar would happen simply if you didn’t spin the chamber after each turn, which would mean the probability of finding a bullet isn’t uncorrelated any more. These details matter. I’d need to work it out to figure how it works, but I picked the game description very deliberately to show the effect I was talking about, so obviously changing it makes things different.
You don’t get told no, you just guess from the fact you’re still alive.
On the contrary, it doesn’t show any such effect at all. It’s carefully contrived so that you can update on the fact you’re still alive, but that happens not to change your strategy. That’s not very interesting at all. Often a change in probabilities won’t change your strategy.
I’m simply showing that with a slight change of setup, updating on the fact your still alive does indeed change your strategy.
If you don’t get told I don’t think it does then, no. It just changes the probabilities in a more confusing way, but you still have no particular way of getting information out of it.
As a player, who by definition must be still in play, you can’t deduce anything from it. You only know what whatever your odds of surviving an extra round were at the beginning, they will go down with time. This probably leads to an optimal strategy that requires you absolutely quit after a certain number of rounds (depending on the probability of the bullet being added). But that’s not affected by any actual in-game information because you don’t really get any information.
You keep on asserting this, but that’s not actually true—do the maths. A player who doesn’t update on them still being alive, will play fewer rounds on average, and will earn less in repeated play. (Where each play is independent).
The reason is simple—they’re not going to be able to play for very long when there are lots of bullets added, so the times when they find themselves still playing are disproportionately those where bullets weren’t added, so they should play for longer.
But the thing is, updating on being still alive doesn’t change anything—it can never drive your estimate of n up and thus save you from losing out. It could convince you to play if you aren’t playing—but that’s an absurdity, if you’re not playing you won’t get any updates! All updating gives you is a belief that since you’re still alive, you must be in a low-bullets, high-probability world. This belief may be correct (and then it’s fine, but you would have played even without it) or wrong (in which case you can never realise until it’s too late). Either way, it doesn’t swing your payoff.
In your added bullets scenario thinking about it there’s a bit of a difference because now a strategy of playing for a certain amount of turns can make sense. So the game isn’t time-symmetric, and this has an effect. I’m still not sure how you would use your updating though. Basically I think the only situation in which that sort of updating might give a genuine benefit is one in which the survival curve is U-shaped: there’s a bump of mortality at the beginning, but if you get through it, you’re good to go for a while. In that case, observing that you survived long enough to overcome the bump suggests that you’re probably better off going on playing all the way to the end.
This is incorrect due to the anthropic undeath argument. The vast majority of surviving worlds will be ones where the gun is empty, unless it is impossible to be so. This is exactly the same as a Bayesian update.
To my understanding, anthropic shadow refers to the absurdum logic in Leslie’s Firing Squad: “Of course I have survived the firing squad, that is the only way I can make this observation. Nothing surprising here”. Or reasonings such as “I have played the Russian roulette 1000 times, but I cannot increase my belief that there is actually no bullet in the gun because surviving is the only observation I can make”.
In the Chinese Roulette example, it is correct that the optimal strategy for the first round is also optimal for any following round. It is also correct if you decide to play for the first round then you will keep playing until kicked out i.e. no way to adjust our strategy. But that doesn’t justify there is no probability update, for each subsequent decision, while all agree to keep playing, can be different. (And they should be different) It seems absurd to say I would not be more confident to keep going after 100 empty shots.
In short, changing strategy implies there is an update, not changing strategy doesn’t imply there is no update.
But the general point I wanted to make is that “anthropic shadow” reflects a fundamental impossibility of drawing useful updates. From within the boundaries of the game, you can’t really say anything other than “well, I’m still playing, so of course I’m still playing”. You can still feel like you update as a person because you wouldn’t cease existing if you lost. But my point was that the essence of the anthropic shadow is that if you think as the player, an entity that in a sense ceases to exist as soon as that specific game is over, then you can’t really update meaningfully. And that is reflected in the fact that you can’t get any leverage out of the update.
At least, that was my thought when writing the post. I am thinking now about whether that can change if we design a game such that you can actually get meaningful in-game updates on your survival; I think having a turn-dependent survival probability might be key for that. I’ll probably return to this.
It seems earlier posts and your post have defined anthropic shadow differently in subtle but important ways. The earlier posts by Christopher and Jessica argued AS is invalid: that there should be updates given I survived. Your post argued AS is valid: that there are games where no new information gained while playing can change your strategy (no useful updates). The former is focusing on updates, the latter is focusing on strategy. These two positions are not mutually exclusive.
Personally, the concept of “useful update” seems situational. For example, say someone has a prior that leads him to conclude the optimal strategy is not to play the Chinese Roulette. However, he was forced to play several rounds regardless of what he thought. After surviving those rounds (say EEEEE), it might very well be that he updates his probability enough to change his strategy from no-play to play. That would be a useful update. And this “forced-to-play” kind of situation is quite relevant to existential risks, which anthropic discussions tend to focus on.
True enough, I guess. I do wonder how to reconcile the two views though, because the approach you describe that allows you to update in case of a basic game is actively worse for the second kind of game (the one with the blanks). In that case, using the approach I suggested actually produces a peaked probability distribution on b that eventually converges to the correct value (well, on average). Meanwhile just looking at survival produces exactly the same monotonically decaying power law. If the latter potentially is useful information, I wonder how one might integrate the two.
We can add anthropic flavor to this game:
1. Imagine this Chinese roulette, but you forget the number N of how many games you already played. In that case, it is more reasonable to bet on a smaller number.
If we add here the idea that firing the gun has only a probability p to broke the vase, we arrive to SSA-counterargument to anthropic shadow recently suggested by Jessika. That is, most of the observations will happen before the risk event.
2 Imagine another variant. You know that the number of played games N=6 and now you should guess n—the number of chambers typically loaded. In that case it is more reasonable to expect n=1 than n=5.
This is SIA-counterargument against anthropic shadow: if there are many worlds, you more likely to find yourself in the world with weakest anthropic shadow.
Note that both counterarguments do not kill anthropic shadow completely, but rather shift it to the most mild variant allowed. I explored it here.
And it all now looks like a variant of Sleeping beauty, btw.
3. However, the most important application of anthropic shadow is the idea of underestimating of the fragility of our environment. Based on previous Ns one can think that the vase is unbrokenable. This may cause a global risks in the case of blindly performing some physical experiment in fragile environment, eg geo-engineering.
Not sure I follow—the idea is that the parameter b gets randomized at every game, so why would this change the optimal strategy? Each game is its own story.
I think this is roughly equivalent to what the blanks do? Now you just have a probability of b+(1−p)(1−b) to not break the vase in case of a loaded chamber.
Only if you know that the games lasted more than one turn! Also this only makes sense if you assume that the distribution that n is picked from before each game is not uniform.
But yeah, things can get plenty tricky if you assume some kind of non-uniform distribution between worlds etc. But I’m not sure with so many possibilities what would be, specifically, an interesting one to explore more in depth.
My point was to add uncertainty about one’s location relative to the game situation—this is how it turns into more typical anthropic questions.
This is one of the few times where I’ve seen a post involving anthropic reasoning, and not come away with the general impression that one-of (myself, the subject itself) is hopelessly confused on some fundamental point. So kudos for that.
In astrophysics they often use expression “observation-selection effect” and it is more clear.
Thanks! I honestly think it actually tends to get all more mind-screwey than needed to be because it always ends up mixed up with all these grand concepts involving death, counterfactual existence and so on. That’s why I wanted to really strip it of all those connotations and keep it super mundane.
Maximizing expected utility in Chinese Roulette requires Bayesian updating.
Let’s say on priors that P(n=1) = p and that P(n=5) = 1-p. Call this instance of the game G_p.
Let’s say that you shoot instead of quit the first round. For G_1/2, there are four possibilities:
n = 1, vase destroyed: The probability of this scenario is 1⁄12. No further choices are needed.
n = 5, vase destroyed. The probability of this scenario is 5⁄12. No further choices are needed.
n = 1, vase survived: The probability of this scenario is 5⁄12. The player needs a strategy to continue playing.
n = 5, vase survived. The probability of this scenario is 1⁄12. The player needs a strategy to continue playing.
Notice that the strategy must be the same for 3 and 4 since the observations are the same. Call this strategy S.
The expected utility, which we seek to maximize, is:
E[U(shoot and then S)] = 0 + 5⁄12 * (R + E[U(S) | n = 1]) + 1⁄12 * (R + E[U(S) | n = 5])
Most of our utility is determined by the n = 1 worlds.
Manipulating the equation we get:
E[U(shoot and then S)] = R/2 + 1⁄2 * (5/6 * E[U(S) | n = 1] + 1⁄6 * E[U(S) | n = 5])
But the expression 5⁄6 * E[U(S) | n = 1] + 1⁄6 * E[U(S) | n = 5] is the expected utility if we were playing G_5/6. So the optimal S is the optimal strategy for G_5/6. This is the same as doing a Bayesian update (1:1 * 5:1 = 5:1 = 5⁄6).
A lot of real games in real life follow these rules. Except, the game organizer knows the value of the vase, and how many bullets they loaded. They might also charge you to play.