A Chess-GPT Linear Emergent World Representation
Introduction
Among the many recent developments in ML, there were two I found interesting and wanted to dig into further. The first was gpt-3.5-turbo-instruct’s ability to play chess at 1800 Elo. The fact that an LLM could learn to play chess well from random text scraped off the internet seemed almost magical. The second was Kenneth Li’s Emergent World Representations paper. There is an excellent summary on The Gradient and a follow-up from Neel Nanda. In it, they trained a 25 million parameter GPT to predict the next character in an Othello game. It learns to accurately make moves in games unseen in its training dataset, and using both non-linear and linear probes it was found that the model accurately tracks the state of the board.
However, this only worked for a model trained on a synthetic dataset of games uniformly sampled from the Othello game tree. They tried the same techniques on a model trained using games played by humans and had poor results. To me, this seemed like a major caveat to the findings of the paper which may limit its real world applicability. We cannot, for example, generate code by uniformly sampling from a code tree. There was also discussion on the implications of this on LessWrong, such as if pretraining should begin with synthetic data to improve interpretability.
So I dug into it. I trained some models on chess games and used linear probes on the trained models. My results were very positive, and answered all of my previous questions (although of course, more questions were generated).
A 50 million parameter GPT trained on 5 million games of chess learns to play at ~1300 Elo in one day on 4 RTX 3090 GPUs. This model is only trained to predict the next character in PGN strings (1.e4 e5 2.Nf3 …) and is never explicitly given the state of the board or the rules of chess. Despite this, in order to better predict the next character, it learns to compute the state of the board at any point of the game, and learns a diverse set of rules, including check, checkmate, castling, en passant, promotion, pinned pieces, etc. In addition, to better predict the next character it also learns to estimate latent variables such as the Elo rating of the players in the game.
All code, data, and models have been open sourced.
Training Chess GPT
My initial hypothesis was that Othello-GPT trained on human games performed poorly due to a lack of data. They only had 130k human Othello games, but the synthetic model was trained on 20 million games. I tried two different approaches to create my datasets: First, I had Stockfish Elo 3200 play 5 million games as White against a range of Stockfish 1300-3200 as Black. Hopefully, this synthetic dataset of superhuman chess bot games would provide higher quality data than human games. Second, I grabbed 16 million games from Lichess’s public chess game database. I trained separate models on individual datasets and various mixes of datasets.
Initially, I looked at fine-tuning open source models like LLama 7B or OpenLlama 3B. However, I almost immediately had to abandon that approach to keep my GPU costs down (I used RTX 3090s from runpod). Instead, I started training models from scratch using Andrej Karpathy’s nanogpt repository. I experimented with 25M and 50M parameter models.
It basically worked on the first try. The 50M parameter model played at 1300 Elo with 99.8% of its moves being legal within one day of training. I find it fairly impressive that a model with only 8 layers can correctly make a legal move 80 turns into a game. I left one training for a few more days and it reached 1500 Elo.
So, gpt-3.5-turbo-instruct’s performance is not magic. If you give an LLM a few million chess games, it will learn to play chess. My 50M parameter model is orders of magnitude smaller than any reasonable estimate of gpt-3.5′s size, and it is within 300 Elo of its performance. In addition, we recently had confirmation that GPT-4′s training dataset included a collection of PGN format chess games from players with an Elo over 1800.
I also checked if it was playing unique games not found in its training dataset. There are often allegations that LLMs just memorize such a wide swath of the internet that they appear to generalize. Because I had access to the training dataset, I could easily examine this question. In a random sample of 100 games, every game was unique and not found in the training dataset by the 10th turn (20 total moves). This should be unsurprising considering that there are more possible games of chess than atoms in the universe.
Chess-GPT’s Internal World Model
Next, I wanted to see if my model could accurately track the state of the board. A quick overview of linear probes: We can take the internal activations of a model as it’s predicting the next token, and train a linear model to take the model’s activations as inputs and predict board state as output. Because a linear probe is very simple, we can have confidence that it reflects the model’s internal knowledge rather than the capacity of the probe itself. We can also train a non-linear probe using a small neural network instead of a linear model, but we risk being misled as the non-linear probe picks up noise from the data. As a sanity check, we also probe a randomly initialized model.
In the original Othello paper, they found that only non-linear probes could accurately construct the board state of “this square has a black / white / blank piece”. For this objective, the probe is trained on the model’s activations at every move. However, Neel Nanda found that a linear probe can accurately construct the state of the board of “this square has my / their / blank piece”. To do this, the linear probe is only trained on model activations as it’s predicting the Black XOR White move. Neel Nanda speculates that the nonlinear probe simply learns to XOR “I am playing white” and “this square has my color”.
Armed with this knowledge, I trained some linear probes on my model. And once again, it basically worked on my first try. I also found that my Chess-GPT uses a “my / their” board state, rather than a “black / white” board state. My guess is that the model learns one “program” to predict the next move given a board state, and reuses the same “program” for both players. The linear probe’s objective was to classify every square into one of 13 classes (blank, white / black pawn, rook, bishop, knight, king, queen). The linear probe accurately classified 99.2% of squares over 10,000 games.
To better interpret the internal predictions of my model, I created some visual heat maps. These heat maps were derived from the probe outputs, which had been trained on a one-hot objective to predict whether a chess piece, such the black king, was present on a given square (1 if present, 0 if not). The first heat map shows the actual board state for the black king. The second heat map depicts the probe’s confidence with a clipping limit applied to the output values where any value above 5 is reduced to 5. This clipping makes the probe’s output more binary, as shown by the white square against the black background. The third heat map presents the probe’s output without any clipping, revealing a gradient of confidence levels. It shows that the model is extremely certain that the black king is not located on the white side of the chessboard.
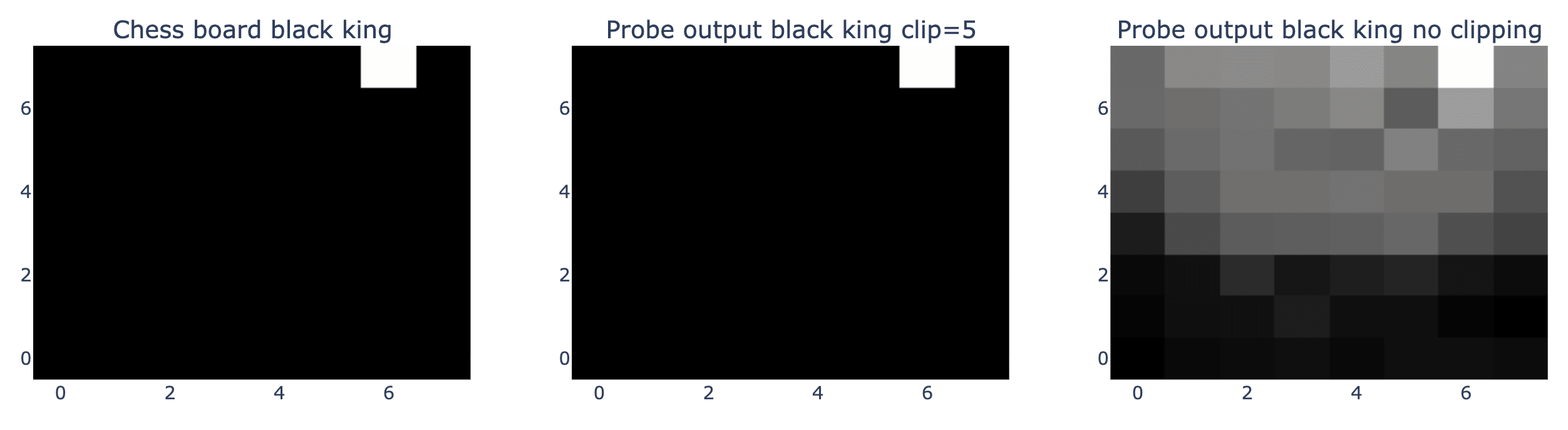
We see a very similar result for the location of the white pawns, although the model is less confident. This board state comes from the 12th move in a chess game, and the model is extremely confident that no white pawns are in either side’s back rank.
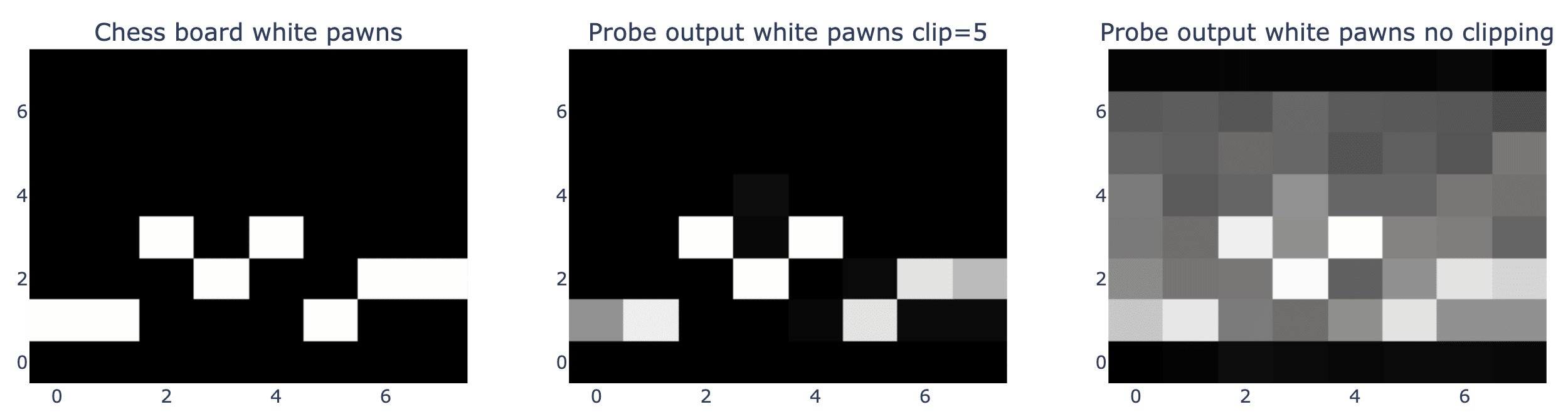
The model still knows where the blank squares are, but it is once again less confident in this.
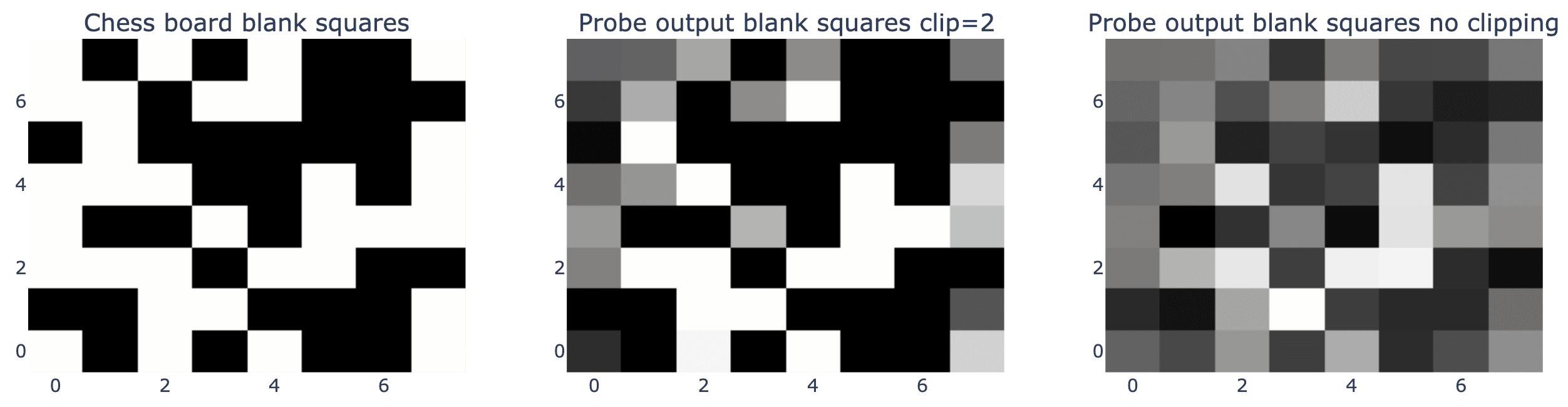
For this move in this chess game, the linear probe perfectly reconstructs the state of the board. The probe’s objective is to classify each square into one of 13 categories, each representing a different chess piece or a blank square. To create this graph, we just take the prediction with the highest value for each square as the probe’s output.
Probing for latent variables
Because Chess-GPT learned to predict the next move in a competitive game, rather than a game uniformly sampled from a game tree, there are interesting latent variables we can probe for. In particular, I hypothesized that to better predict the next character, it would learn to estimate the skill level of the players involved.
Initially, I trained the probe on a regression task, where its task is to predict the Elo of the White player. It would do this by training on the internal activations of the model between moves 25 and 35, as it would be extremely difficult to predict player skill early in the game. However, the majority of the games in the Lichess dataset are between 1550 Elo and 1930 Elo, which is a relatively narrow band. The linear probe trained on Chess-GPT had an average error of 150 Elo, which seemed good at first glance. However, a linear probe trained on a randomly initialized model had an average error of 215 Elo. The narrow window of Elo in most games made it difficult to discern the model’s level of knowledge. Distinguishing between a 1700 and 1900 Elo player just seems like a very difficult task.
So, I then trained the probe on a classification task, where it had to identify players below an Elo of 1550 or above an Elo of 2050. In this case, the probe performed much better. A probe trained on a randomly initialized model correctly classified 66% of players, while a probe trained on Chess-GPT correctly classified 89% of players.
To an extent, this is unsurprising. This reminds me of the OpenAI’s 2017 Sentiment Neuron paper. In it, they trained an LSTM to predict the next character in Amazon reviews. When they trained a linear probe on the model’s internals using just 232 labeled examples, it became a state of the art sentiment classifier. OpenAI wrote then that “We believe the phenomenon is not specific to our model, but is instead a general property of certain large neural networks that are trained to predict the next step or dimension in their inputs”. With this context, it’s almost an expected result.
Potential future work
The step that I am currently working on is performing casual interventions using these linear probes and Contrastive Activation Addition to further validate my work. I’m seeing promising early results, and plan on writing up my results within the next couple of weeks.
As Neel Nanda discussed, there are many advantages to interpreting models trained on narrow, constrained tasks such as Othello or Chess. It is difficult to interpret what a large LLM like Llama is modeling internally when predicting tokens in an unconstrained domain like poetry. There has been successful interpretation of simple models trained on toy tasks like sorting a list. Models trained on games provide a good intermediate step that is both tractable and interesting.
In particular, there are interesting implications for testing different intervention strategies. There are many decisions to make and details to track when implementing interventions. Using a Chess model, we can quickly test many strategies to see if it’s doing the thing we want (such as improving the model’s Elo) without harming existing capabilities (making legal moves).
Another thought is to look for some sort of internal tree search. When I play chess, I perform a sort of tree search, where I first consider a range of moves, then consider my opponent’s responses to these moves. Does Chess-GPT perform a similar internal calculation when predicting the next character? Considering that it is better than I am, it seems plausible.
Other potential directions:
- Investigate why the model sometimes fails to make a legal move or model the true state of the board.
- How does the model compute the state of the board, or the location of a specific piece?
- I fine-tuned GPT-2 on a 50 / 50 mix of OpenWebText and chess games, and it learned to play chess and continued to output plausible looking text. Maybe there’s something interesting to look at there?
Open source code, models, and datasets
All code, models, and datasets are open source. To train, test, or visualize linear probes on the LLMs, please visit: https://github.com/adamkarvonen/chess_llm_interpretability
To play the nanoGPT model against Stockfish, please visit: https://github.com/adamkarvonen/chess_gpt_eval/tree/master/nanogpt
To train a Chess-GPT from scratch, please visit: https://github.com/adamkarvonen/nanoGPT
All pretrained models are available here: https://huggingface.co/adamkarvonen/chess_llms
All datasets are available here: https://huggingface.co/datasets/adamkarvonen/chess_games
Wandb training loss curves and model configs can be viewed here: https://api.wandb.ai/links/adam-karvonen/u783xspb
99.2% square accuracy is consistent with 50% position accuracy. Did you check position accuracy?
I think OpenAI models are intentionally trained on a ton of chess.
Yes, in this recent OpenAI superalignment paper they said that GPT-4′s training dataset included a dataset of chess games filtered for players with greater than 1800 Elo. Given gpt-3.5-turbo-instruct’s ability, I’m guessing that its dataset included a similar collection.
Very cool work! I’m happy to see that the “my vs their colour” result generalises
Saw your update on GitHub: https://adamkarvonen.github.io/machine_learning/2024/03/20/chess-gpt-interventions.html
Awesome you expanded on the introspection.
Two thoughts regarding the new work:
(1) I’d consider normalizing the performance data for the random cases against another chess program with similar performance under normal conditions. It may be that introducing 20 random moves to the start of a game biases all players towards a 50⁄50 win outcome. So the sub-50 performance may not reflect a failure of flipping the “don’t suck” switch, but simply good performance in a more average outcome scenario. It’d be interesting to see if Chess-GPT’s relative performance against other chess programs in the random scenario was better than its relative performance in the normal case.
(2) The ‘fuzziness’ of the board positions you found when removing the pawn makes complete sense given one of the nuanced findings in Hazineh, et al Linear Latent World Models in Simple Transformers: A Case Study on Othello-GPT (2023) - specifically the finding that it was encoding representations for board configuration and not just pieces (in that case three stones in a row). It may be that piecemeal removal of a piece disrupted patterns of how games normally flow which it had learned, and as such there was greater uncertainty than the original board state. A similar issue may be at hand with the random 20 moves to start, and I’d be curious what the confidence of the board state was when starting off 20 random moves in and if that confidence stabilized as the game went on from there.
Overall really cool update!
And bigger picture, the prospects of essentially flipping an internalized skill vector for larger models to bias them back away from their regression to the mean is particularly exciting.
Both are great points, especially #1. I’ll run some experiments and report back.
I had the following results:
Stockfish level 2 vs Stockfish level 0, 0.01 seconds per move, 5k games:
0 random moves: win rate 81.2%
20 random moves: win rate 81.2%
40 random moves: 77.9%
95% confidence interval is about +- 1%
Stockfish level 15 vs level 9, 0.01 seconds per move, 5k games:
0 random moves: 65.5%
20 random moves: 72.8%
40 random moves: 67.5%
Once again, 95% confidence interval is about +- 1%
At 120 seconds per move, both of these level differences correspond to ~300 Elo: https://github.com/official-stockfish/Stockfish/commit/a08b8d4
This is 0.01 seconds per move. It appears that less search time lowers the Elo difference for level 15 vs level 9. A 65% win rate corresponds to a ~100 Elo difference, while a 81% win rate corresponds to a 250-300 Elo difference.
Honestly not too sure what to make of the results. One possible variable is that in every case, the higher level player is White. Starting in a game with a random position may favor the first to move. Level 2 vs level 0 seems most applicable to the Chess-GPT setting.
Interesting results—definitely didn’t expect the bump at random 20 for the higher skill case.
But I think really useful to know that the performance decrease in Chess-GPT for initial random noise isn’t a generalized phenomenon. Appreciate the follow-up!!
Remember that cute little clicker game about a Paperclip Maximizer? The chessGPT learning to estimate ELO really reminds me of the concept of Yomi (reading the mind of the enemy) as used in that game.
Were the results basically the same in all cases? Or e.g. was the all-stockfish-data engine less robust to off-distribution inputs?
The all stockfish data engine played at a level that was 100-200 Elo higher in my tests, with a couple caveats. First, I benchmarked the LLMs against stockfish, so an all stockfish dataset seems helpful for this benchmark. Secondly, the stockfish LLM would probably have an advantage for robustness because I included a small percentage of stockfish vs random move generator games in the stockfish dataset in the hopes that it would improve its ability.
I haven’t done an in depth qualitative assessment of their abilities to give a more in depth answer unfortunately.
Really, really cool. One small note: It would seem natural for the third heatmap to show the probe’s output values after they’ve gone through a softmax, rather than being linearly scaled to a pixel value.
That’s an interesting idea, I may test that out at some point. I’m assuming the softmax would be for kings / queens, where there is typically only one on the board, rather than for e.g. blank squares or pawns?
Did you notice any kind of deception? If it knows the rules, but chooses to break them to its own benefit, it could be a very lucid example of motivated deception.