On New York’s Antibody Tests

Previously: My Covid-19 Thinking: ⁴⁄₂₃ pre-Cuomo Data which has links to other previous stuff at the top.

We’re all working from the same information, mostly from Cuomo’s slides. Let’s reproduce them here, give the rest of the information, then go from there.

What We Know

Also in 2 other slides:

52% female sample with 12% positive, 48% male with 15.9% positive.

Asian 8.8% of total with 11.7% positive, black 14.3% with 22.1% positive, Latino 17.6% of total with 22.5% positive, and white 57.1% of total with 9.1% positive. Cuomo says this is mostly because most non-whites in the state live in New York City.

Samples were taken at grocery stores. From the comment that this ‘missed essential workers’ I presume it happened during work hours. People were given their results if they wanted to know, and participation was voluntary.

So many questions. Still, very good data. Many thanks for providing it. What does it all mean?

Mostly people seemed surprised the numbers were so high, and a lot of people objected the infection rate couldn’t possibly be so high, and thus started looking for evidence it wasn’t so. As opposed to my reaction, which was that the rate seemed too low so there were probably things I needed to adjust for. My pre-study best guess was as follows, as posted yesterday:

That would make the infection rate in New York State overall about 19% now and 29% when things are finished. We’d have identified 13.3% of positive cases as of right now, with vastly inadequate testing.

This would also imply New York City was roughly 30% infected, which is on the extreme low end of my previous prior guess range.

That now seems fully compatible with the results of the antibody tests. Alas, part of the problem with that compatibility is that there’s a wide range of potential ways the results could be biased.

Nate Silver had a good twitter thread outlining the three big problems with the numbers. The numbers lag, there was a biased sample (we just don’t know in what direction or how big a bias) and not knowing the specificity/sensitivity of the test.

By contrast, there have been lots of links from people who should know better to a pretty bad Twitter thread by Anish Jha, who was quick and has reasonable credentials and claim to authority and made noises that sounded like being “responsible” – he speculates about what would happen if sensitivity was only 93% in a test that was only 3.6% positive for almost 1000 people in 32% of the state, which caused me to have a would-facepalm-except-not-touching-face moment. I did the informal version of pointing this out (a reply pointing out the obvious) as soon as I saw the thread. The sufficiently formal version of pointing this and some other remarkably basic things out was done by Venk Murthy here.

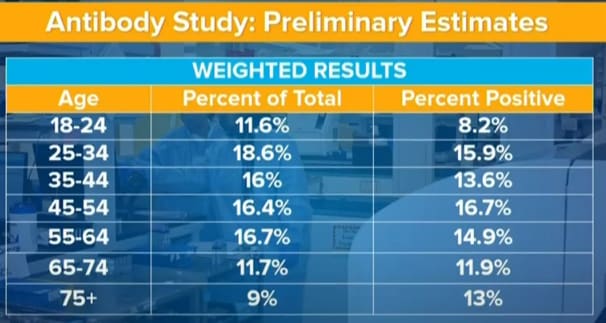
We won’t discuss the age, gender or ethnicity breakdowns at all beyond the implications for children. Infections by age didn’t vary much, although they might vary more once you account for how the sample is biased, in ways that are again hard to figure out. Gender data matches previous findings so it’s not giving us much to discuss. The ethnic numbers are, Cuomo says, mostly a function of NYC vs. the rest of the state, which makes them too confounded to say too much without cross-tabs. If we did get the cross-tabs, we’d be in a better position to say more on that.

Specificity

How specific is this test? To what extent are false positives an issue? It would be good to tackle that question first.

We have a naive lower bound on specificity from the 3.6% positive rate upstate. In theory, without further evidence, we have to presume that maybe none of those people were positive plus a margin for error. In practice, that’s obviously not what we should be guessing. Once we know that we have a 21% positive rate for New York City on the same test with the same procedure, we can use the ratio of infections in the two places to figure out what range of false positive rates is plausible.

We have a list of deaths and confirmed infections by county here, from The New York Times. There are 780 reported deaths and 21,043 confirmed infections in Rest of State (hereafter “upstate”) versus 16,161 reported deaths and 271,578 confirmed infections in Long Island, New York City, Rockland and Westchester (hereafter “downstate”). This gives upstate a lower CFR (3.71% vs. 5.95%) which partly reflects better testing (e.g. positive test percents have been lower) and may also represent better results due to non-overwhelmed hospitals, but also may reflect reduced under-reporting of deaths.

To be conservative on multiple levels, we’ll use deaths – the downstate death rate is likely somewhat higher, but they’re also probably under-reporting most of those extra deaths. Upstate has 35.8% of the state’s population, versus 64.2% for downstate. It has 4.6% of reported deaths. Thus, naively we should expect the true upstate infection rate to be 8.6% of the downstate rate, and false negatives should cancel each other out here once we remove false positives. In the antibody tests, 18.9% of downstate was positive. Thus, we assume that (0.189 – FalsePositiveRate)*0.086 = (0.036 – FalsePositiveRate).

The false positive rate is therefore about 2.16%, give or take margin of error, and worries that test sites upstate were not representative (which could go in either direction).

(We could and someone really should attempt to improve this by adjusting all the numbers for various things, but I’ll consider that task beyond scope here.)

That’s a lot! Upstate this implies the majority of positive results are false positives.

In the context of “21% of New York City” however, it’s not a lot. It’s still 19% of New York City, and a 90% chance that a positive is real.

How much of that 2.1% could be eliminated in individual cases by doing a second test? That depends. If we have a test that’s looking for some of the wrong antibodies along with the right ones, and you have the wrong ones it is looking for, you’ll always show positive. If it’s other kinds of error, it won’t repeat. If it’s that the test is sort of responsive to other antibodies, then you’ll get something in between.

[TODO check with Dad to see how optimistic to be here]

Sensitivity and Lag

What about false negatives? The good news is we were able to solve for false positives without worrying about the false negative rate. The bad news is that the false negative rate is an open-ended source of bias that could be tiny and could be huge. In theory it allows us to claim that the true rate could be arbitrarily higher than what is reported, up until we hit the barrier that true positive rates can only go so high in their highest areas.

We could, of course, find a group of people who definitely had Covid-19 because they tested positive and had lots of symptoms and were hospitalized, then recovered a month ago, test them for antibodies, and get the answer that way. Mostly. We should do that yesterday. However, false negative rates might be different for different groups that have different antibodies or different antibody rates, so that number might be modestly too high.

For now, given what I know of such tests, I’m going to presume that the false negative rate for those infected a long time ago is low, let’s say it’s also 2%.

And then there’s the lag issue.

We do know of one huge source of false negatives. It takes (something like) two weeks for antibodies to show up. A person infected a few days ago will test negative on the antibody test. We can add to that about a two day turnaround on the tests, which were announced on Thursday ⁴⁄₂₃.

Thus, we should roughly treat the test as showing the cumulative infection rates sixteen days prior, which is ⁴⁄₇.

We’ll come back later to what that means about current rates.

Warnings Against Using Antibody Tests are Obvious Nonsense

Before we return to the calculations, I want to briefly shame everyone who is trying to look responsible by warning people not to use the results of the antibody tests on a personal level due to possible mistakes. What if someone got a wrong result and did something they shouldn’t?

I hereby declare a new rule that these people are no longer allowed to put on pants. We can’t be confident the pants are clean. They might be dirty, there’s always some measurement error, so we have to always assume all their pants are dirty. So no pants for them. Sorry.

If you give someone 98% accurate information about whether they have antibodies to Covid-19, they will make much better decisions than if they lacked that information, both personally and for society. If we put such people into positions where they are likely to be exposed and expose others, instead of other people, we will save lives. Doing so will help save our jobs, our economy, our future, and with it our ability to continue saving and living lives.

There is also the concern trolling that perhaps such people are not immune to reinfection. They are probably immune for a long time. And they are almost certainly immune for now. We need to make decisions now. We need to live our lives now.

Yes, we’d rather run a better or second test and be 99.8% sure instead, if we had that option, but we do what we can with what information we do have. And for now, we’d much rather test two people once than one person twice.

I could go on but feel no need to do so. We now return to crunching the numbers.

Copenhagen interpretatione nisi ethicam antecellere delenda est.

Bias and Sampling Error

That was the easy part. The hard part is correcting for bias, in both directions.

We know how to collect mostly random samples (minus the refusal rate) by using things like phone directories. New York didn’t do that. They set up shop in grocery stores, during work hours (I think), and took volunteers using an unknown (to me for me) procedure.

I want to be clear. I am very happy they did that!

Don’t let the perfect be the enemy of the good! Viva la speed premium! Move fast and break things! Do science to it!

It does leave us a bit of a puzzle to solve.

Possible hypotheses I could come up with after two days on how this sample might be importantly biased:

Grocery stores chosen might be not random, or not weighted properly by how many people use them.
Procedures in different places might be different.
People who have had symptoms, or who were otherwise higher/lower risk, might have a different probability of joining the sample conditional on going to the grocery store. Especially since test results were given to individuals afterwards.
Essential workers were working and thus mostly missed, because the data was gathered mostly/entirely during work hours.
Dead people don’t buy groceries.
Sufficiently sick people don’t buy groceries in person. Anyone with symptoms hopefully stayed home.
Institutionalized people don’t buy groceries. Anyone in a nursing home, or prison, will be excluded.
Sufficiently rich and/or cautious people who can afford delivery won’t go to the grocery store.
Instacart workers would be vastly over-represented. Always shopping! May have been excluded from sample intentionally or have been working and thus unable to stop to join study.
People who batch grocery shopping would go less often and be underrepresented, and also mostly be more responsible presumably. Whereas those who go every day or two will show up more often and be over-represented.
Children weren’t tested at all, presumably for legal reasons.

Location selection could have been weird in any number of ways. It might be especially weird upstate, potentially impacting our specificity calculation. I see no reason to assume it points in one direction rather than the other. It seems more like extra noise.

The basic pattern is that the people at highest risk are not in the sample, and the people who are at lowest risk are also not in the sample. The sample concentrates among those at medium risk, and potentially over-represents the ones among them taking more risk rather than less risk.

The more you think grocery stores are themselves an important remaining point of risk the more you’d be inclined to think that the sample is artificially high risk. I think grocery stores are the highest risk activity that many, perhaps most, of us still engage in outside of essential workers. But I also think that the few remaining high risk actions are where the bulk of remaining probably risk lies.

Naively, it’s tough to know which effect dominates.

Not testing children is odd. We don’t know how often they get infected because we don’t bother testing them. I could believe a world where they are very hard to infect and are basically always negative. I could also believe a world in which they are in relatively large households and are incapable of taking proper precautions, and thus get infected reasonably often. The 8.2% infection rate for ages 18-24 is suggestive of lower rates, but also could largely reflect the conditions of college students. Infection rates and age seem mostly uncorrelated in this data, so my guess is that child infection rates are if anything lower, but not that dissimilar to overall rates because they get secondary household infections a lot. We really don’t know, and given legal conditions, probably will never know.

Instacart workers are very high risk, along with other delivery services workers, but how many are in the sample? Possibly none, if they excluded them. Possibly a lot. Instacart has more than 500k full-time shoppers nationwide. In-store personal shoppers are employees of the store and thus presumably excluded from the study. Presumably NY has more than its share of Instacart by a lot, but I don’t know how much more, as it is available across the country and most people are locked down one way or another. My guess is this isn’t that big a factor.

The bigger questions are, how many high risk people are excluded, how many low risk people are excluded, and how high risk slash low risk are those groups relative to the medium risk group.

My prior is that high risk groups are at much higher risk than medium risk groups. High risk groups seem naively like they have at least an order of magnitude more exposure points, and have those points with people who themselves are also far more likely to be higher risk themselves. If people go about their normal business, R0 = 4 is a general estimate, R0 = 8 for New York City, higher for poor areas. Compare that to average R0 ~ 0.84 right now (I said 0.85 yesterday, last two days data has been good) for the state now. An order of magnitude seems like the low end estimate.

My prior is that low risk groups are similarly at much lower risk than medium risk groups. People who are fully isolating properly, including avoiding grocery stores entirely for their entire quarantine house if any, are taking at least an order of magnitude less risk than those who are grocery shopping, if only from the grocery shopping. The risk isn’t zero, but it might be not that dissimilar once those in question locked down. Some of them will have gotten sick before locking down, and either not know it or not be confident enough in it to not isolate.

So probably:

The very low risk group is large, its risk is very low, and their rate of participation is also very low here. They’re basically not using grocery stores except via pick-up and delivery, and are excluded from the study.
The medium risk group is the large majority, their rate of participation is normal. They all use the grocery stores. Their risk is probably substantially lower than average.
The high risk group includes essential workers and those who can’t or won’t properly distance (or didn’t do so for a while earlier, and thus are at much higher retrospective risk). Essential workers from this group are not in the sample much, but some are, such as restaurant workers shopping in the morning.

My guess is that this process ends up making the resulting group lower risk than average, based purely on who ever gets included rather than rates of inclusion. There are some big exclusion groups at very high risk. Very hard to quantify all this, of course, and could go either way.

The higher risk someone is, however, the more often they likely use the grocery store given they go at all. The (I hope small) group that goes to grocery stores every day or two is a scary one.

Then there’s selection within the store. If you think you’ve been positive, that’s a reason to want an antibody test. However, everyone should want an antibody test if they’re freely available, because the upside on learning you were asymptomatic and recovered is that you get to resume normal activities, or at least adjust your risk level if you are worried about false positives. Plus it was doubtless made clear they wanted to test presumed negative people, so anyone doing this would be helping save lives. People who are generally careful about risk should also likely be more inclined to want the information, and to want to help out with the study.

Thus, for now, I’m going to do no correction for bias in either direction. I’m not confident enough in direction to do that, let alone magnitude. This does point to where we’d like to do studies next to improve our knowledge. Doing more grocery store sampling would be nice, but 3000 is already a reasonable sample. I’d rather spend my efforts now on testing essential worker samples, especially hospital workers but also others, and those who can’t go to the grocery store. Also we should make an effort to quantify the sizes of such groups, and also the excluded low-risk group. Antibody testing the low-risk group as well would be a bonus.

Another idea is to now do the phone directory study, but ask people how often they go to the grocery store and at what times when collecting samples! Then we can figure out how to correct the samples, which lets us take better advantage of what we have, and also lets us gather more samples at grocery stores and get good use out of them.

Now that we’ve discussed sample bias, sensitivity/specificity and lag, we’re ready to put it all together and reconcile it with the analysis I made before seeing the results.

The Model

We also update our previous model with several additional days of data. The recent news from New York and also he whole United States has been good, because test numbers have gone up. 24.1% and 23.4% positive rates for ⁴⁄₂₃ and ⁴⁄₂₄ respectively in New York are big progress over previous rates. We haven’t seen numbers that low since ³⁄₁₉, which means well before the lock down. We do need to adjust somewhat for the testing surge, but even so we’re progressing well. I’ve lowered my R0 estimate from 0.85 to 0.83 before we continue, also to account for the expectation of gradual drop in R0 due to herd immunity effects over time.

As a reminder, the model assumed a 1% IFR, a 50% under-count of deaths, a 21 day delay from infection to death, a 5 day serial interval, a 2.5 day doubling time before lockdown, that the positive test rates were never that much higher than the point where they stop becoming meaningful even at their peak, and a 5 day delay in testing new infections.

If we total the infections in that model up to and including ⁴⁄₇, we get 2.57 million, or 13.2% infected.

If we get infections at that time from the antibody tests, and add the 1% death rate and 2.2% false positive and negative rates, we get 11.9% infected.

That is well within the range of plausible bias in data collection, not to mention the huge error bars in what I’m doing via seat of pants. It all seems very reasonable.

The model with the R0 adjustment now predicts that we currently have 3.8 million infections in New York State, or 19.5% overall infection rate. If we did a 10% adjustment down to fully accept the antibody result, we would get 17.7%. Given the new R0, the model projects the final infection count if we fully squash at this rate forever to be 310k additional infections, for a final count of 21.1% infected or 19.0% after adjustment, and a death count of 41,123 before adjustment or 37,010 with the adjustment. Like all models, any second wave after reopening isn’t included. Model thinks about 24,000 have already died because it thinks there’s a 50% under-count that will likely never be corrected.

I have no doubt my model could be improved, and to extent I have time I will work on improving it and on getting useful bounds on areas outside of New York using similar methods. The biggest place to move things around is that the IFR could be lower than 1%, which would proportionally raise infection rates, or possibly that it’s a little higher – the range of numbers that don’t lead to major contradictions are roughly 0.3% to 1.5%. However, the data has now come in on enough front that I see tight error bars on the New York situation. The antibody study only confirms this even more.

Now let’s do more tests!