Some time after writing Classifying games like the prisoner’s dilemma, I read a paper (I forget which) which pointed out that these games can be specified with just two numbers.
Recall that they have the following payoff matrix:
| Player 2 | |||
|---|---|---|---|
| Krump | Flitz | ||
| Player 1 | Krump | ||
| Flitz |
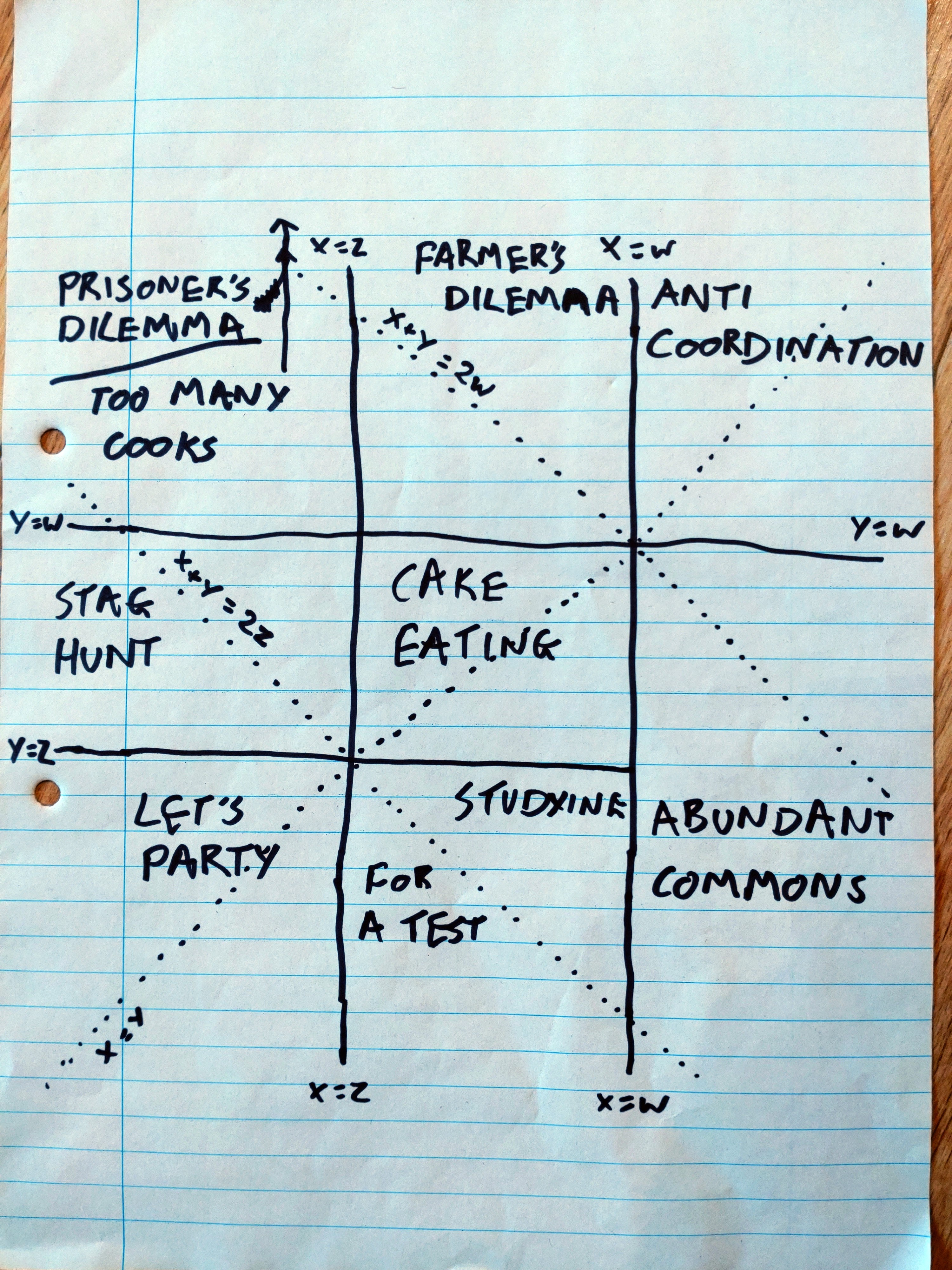
where .[1] We can apply a positive affine transformation (that is, where ) to all of without changing the game. So let’s pick the function . This sends to and to , leaving us with just two parameters: and .
So what happens if we plot the space of these games on a graph? The lines become , i.e. vertical and horizontal lines. The lines and become the diagonals and ; and becomes the diagonal . Drawing those lines, and relabelling in terms of , it looks like this:
Note: I tried to limit the vertical size of that but couldn’t figure out how. Sorry!
Note that Cake Eating (my favorite game) is the only one with a finite boundary; the other boxes extend to infinity. There are also finite components in the Farmer’s Dilemma (with ), and Stag Hunt and Studying For a Test (with ). As drawn, Prisoner’s Dilemma occupies almost all of the box it shares with Too Many Cooks; but Too Many Cooks (above the line ) is also infinite. (I initially got those the wrong way around, so the drawing isn’t very clear there.)
I don’t know if we learn much from this, but here it is.
- ↩︎
In the previous post I mostly ignored equalities because it was mildly convenient to do so. But the analysis here completely fails if we allow . So now I’m ignoring them because it’s considerably more convenient to do so.
Loosely and non-rigorously, x/0 is infinite, and so all games with W=Z are extreme forms of the corner games (unless X=W=Z or Y=W=Z). X~Y>W=Z gets you an anti-coordination game and W=Z>X~Y gets you a pure or relatively pure coordination game (Let’s Party).
Y>W=Z>X and X>W=Z>Y are interesting, because they equate games as different as the PD (or Too Many Cooks) and Abundant Commons. I would describe this game as more similar to the Abundant Commons than the PD, as Flitz/Flitz is a perfectly acceptable equilibrium. The value transfer here is neither hyperefficient nor inefficient, but merely efficient.
The triple equalities here are equivalent under name change, so, WLOG, let’s take X=W=Z. Then, there are two games: Y>X and Y<X. Looking at the diagram, X=W=Z>Y should resemble Studying for a Test, while Y>X=W=Z should resemble the Farmer’s Dilemma.
The former game has a primary theme of avoiding Y, and so, while Flitz/Flitz is an equilibrium, I would expect to see more Krump/Krump, as it is never beneficial to play Flitz when there’s any risk of Krump.
The latter game is more complex, but the equilibrium you actually see is Flitz/Flitz, because the only way to get Y is if you play Flitz.
Finally, with all four equal, there is no longer much of a game. All strategies are equilibria, the payoff is identical in each case. This is the trivial game.
Expanding on the Y>W=Z>X and X>W=Z>Y, I would split Abundant Commons at Y=Z, into Abundant Commons above the line and Deadlock below it. Then, the games equated are Deadlock and the PD, and those form a natural continuum.
I’m not familiar with all these games by name, and feel like the post would be better with some explanations. I’m particularly confused by how Y very negative and X very positive becomes ‘abundant commons’. Attempting to Google ‘abundant commons game’ doesn’t immediately clarify.
These are all explained (albeit very briefly) in philh’s original essay, mentioned in the first sentence.
Ah indeed, thank you!