Practicing Bayesian Epistemology with “Two Boys” Probability Puzzles
The Puzzles
There’s a simple Monty Hall adjacent probability puzzle that goes like this:
Puzzle 1
I have two children, at least one of whom is a boy. What is the probability that both children are boys?
A more complex variation recently went viral on Twitter:
Puzzle 2
I have two children, (at least) one of whom is a boy born on a Tuesday — what is the probability that both children are boys?
Then Isaac King tweeted an even more complex variation:
Puzzle 3
I have two children, at least one of whom is a boy born on a day that I’ll tell you in 5 minutes. What is the chance that both are boys, and what will the chance be after I tell you the day?
All three versions are fun and worth a try if you want to learn and practice Bayesian reasoning.
Personally, I found Isaac’s version MUCH harder than the others. I was surprised how hard it stumped me since I had a pretty easy time with the first two (LessWrong trained me well). As I stared at it for longer than I want to admit, the gears of my brain kept jamming. I couldn’t see a coherent non-paradoxical story for what the Bayesian updates should look like.
I recommend giving Puzzle 3 a try before reading my solution.
By the way, I tested it on GPT-o1 and Claude 3.5 Sonnet and they only give incorrectly-reasoned wrong answers. It’ll be interesting to see if o3 can do better.
The Solution
First, when we hear the “I have two children, at least one of whom is a boy” part, we set the probability of two boys to 1⁄3 because the possibilities {(boy, girl), (girl, boy), (boy, boy)} are a-priori equally likely and we haven’t had a reason to update their relative likelihoods.
Then when we hear “I’ll tell you the day that at least one was born on”, we don’t need to update the three relative likelihoods because it’s a statement we were equally likely to hear in all three possible worlds.
Now the tricky part…
When we subsequently hear a particular day, e.g. “Friday”, how should we update the relative probabilities?
It seems like we shouldn’t update, because hearing any weekday was a-priori equally likely to hear, and if hearing any weekday was going to update us in any particular direction, why couldn’t we have just made that update before we heard the particular day?
In other words, why wouldn’t we pretend like the parent mumbled the day and we couldn’t make out the word, but update anyway, since it’s going to be the same update regardless of which day he says?
Indeed, the correct answer is going to be that hearing the particular day doesn’t trigger an update. The correct answer to the puzzle is the intuitive one…
ANSWER:
The probability that both children are boys stays 1⁄3 the whole time
Now the confusing part...
The confusing part is that when we compare the answer of “don’t update on the birth day of the week information” to Puzzle 2′s answer, it seems inconsistent or paradoxical.
Puzzle 2 asks:
I have two children, (at least) one of whom is a boy born on a Tuesday—what is the probability that both children are boys?
Puzzle 2′s answer is larger than 1⁄3; the (boy, boy) world gets more likelihood for being more consistent with the evidence of having at least one boy born on a Tuesday: 13⁄49 for (boy, boy), compared to 1⁄7 (i.e. 7⁄49) each for (boy, girl) and (girl, boy).
The posterior probability of the (boy, boy) world is thus 13 / (13 + 7 + 7) = 13⁄27.
But why doesn’t this same visualization and this same calculation apply to the new puzzle (Isaac’s twist)? If we hear “Tuesday” in the new puzzle, shouldn’t we similarly update our probability of two boys from 1⁄3 to 13⁄27 ???
IMO this is quite a juicy apparent paradox, and gets to the heart of why most people underestimate Bayesian epistemology. People don’t realize how subtle and powerful it is when wielded by a trained practitioner.
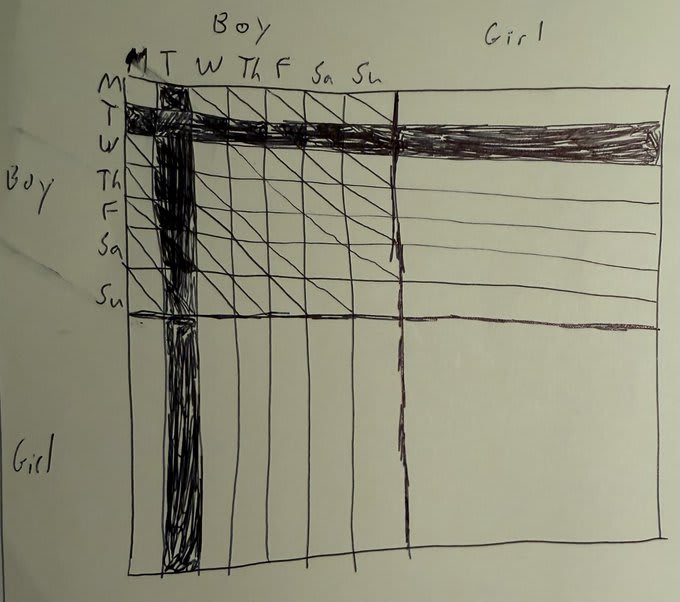
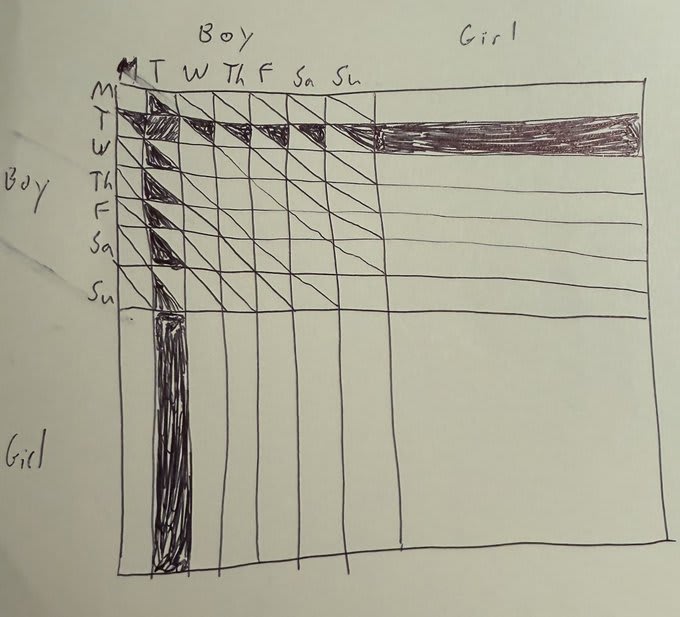
Let’s think about the scenarios that make the parent in the new puzzle say “Tuesday”:
We’re in the (boy, girl) world and the boy is born on Tuesday
We’re in the (girl, boy) world and the boy is born on Tuesday
We’re in the (boy, boy) world and only the older boy is born on Tuesday
We’re in the (boy, boy) world and only the younger boy is born on Tuesday
We’re in the (boy, boy) world and both boys are born on Tuesday
So far, the diagram above that we used for the original puzzle still looks like it models the situation…
The key is to realize that in scenarios #3 and #4, we don’t always hear the parent say “Tuesday”. Half the time, we hear the parent say the name of the weekday that the other boy was born on!
In the diagram below, the shading of squares in the (boy, boy) quadrant doesn’t just represent the fraction of scenarios wherein the parent could say “Tuesday”, it represents the probabilistically weighted fraction of scenarios wherein the parent does say “Tuesday”:
The shaded half-squares conveniently make the (boy, boy) quadrant’s shaded part add up to 1⁄49 + 12(0.5/49) = 7⁄49, just like the (boy, girl) and the (girl, girl) quadrants’ masses do, allowing us to rationally answer the puzzle with our a-priori probability of 1⁄3.
QED
More Bayesian analysis
Now that we’re over the hump — problem solved, paradox resolved — let’s see what insights we can glean about Bayesian reasoning.
Consider the humble Puzzle 1:
I have two children, at least one of whom is a boy. What is the probability that both children are boys?
I explained above that it’s 1⁄3 because the possibilities {(boy, girl), (girl, boy), (boy, boy)} are equally likely.
But in fact, the parents I know are much more likely to ask you that question in the first place in worlds where they have two boys. Then they’ll smirk and say “wanna bet?” and you’ll lose the bet.
But if you don’t see that coming, don’t blame Bayesian reasoning; blame your own lack of mastery of Bayesian reasoning. If the naive calculation gives you 1:2 odds of (boy, boy), but your understanding of parent humor tells you it’s 3 times more likely that parents with two boys would spring that puzzle on you, then you should actually be assigning 3:2 odds of (boy, boy), not 1:2.
You might be thinking: Fine, but can’t “I have two children, at least one of whom is a boy; what’s the probability that both are boys” still be interpreted as a problem of pure math? Why go on a tangent to talk about real-life parents?”
Well, actually the puzzle statement contains a default assumption which — while clear enough — is not at the level of a rock-solid default assumption to accept.
The implied assumption is about how the reality of the parent’s kids affects what the parent says to you. Basically:
If we’re in the (boy, girl), (girl, boy) or (boy, boy) world, then the parent asks you the puzzle.
If we’re in the (girl, girl) world, then the parent says nothing or asks you a different puzzle, perhaps one about girl children.
But consider an alternative assumption. What if we assume that the relationship between the reality of the parent’s kids and the puzzle he gives you is as follows:
If we’re in the (boy, boy) or (girl, girl) world, then he challenges you with the puzzle about his boy or girl children, respectively.
If we’re in the (boy, girl) or (girl, boy) world, then he randomly selects which gendered version of the puzzle to challenge you with.
Let’s assume the parent operates in this “equal-opportunity gendered puzzle” mode, and now consider what it means when he asks you Puzzle 1:
I have two children, at least one of whom is a boy. What is the probability that both children are boys?
It’s still true that {(boy, girl), (girl, boy), (boy, boy)} were a-priori equally likely possibilities. But now you have to consider that half the probability of the (girl, boy) or (boy, girl) worlds flowed into worlds where the parent gives you the girl version of the puzzle, so only half the original probability of those squares flows into the world where you receive the evidence of the parent giving you the particular puzzle that you’re hearing.
Under our new assumption, the answer to the easy puzzle is arguably more intuitive than the result of the original puzzle: The probability that the parent has two boys is 1 / (1 + 0.5 + 0.5) = 1⁄2, not 1⁄3.
Ok, but why is the “default assumption” the one that gets you 1⁄3 as the answer to the easy puzzle? Especially since it’s the less intuitive answer (IMO)?
I think it’s because any time you hear a piece of information in a math puzzle context, you’re supposed to assume that the correct way to calculate a posterior probability is to just count the number of possible world-states that are logically consistent with the puzzle’s new object-level proposition. You do this kind of count twice to get probability as a fraction: once for the numerator and once for the denominator. I hear there are some quirky people called “frequentists” who consider the non-Bayesianness of the default interpretation to be a feature, not a bug, of these kinds of puzzles.
When Isaac twisted the puzzle by having the parent send us different pieces of information at different times, he made it impossible to only perform updates on the explicit content of the parent’s words, because it’s necessary to incorporate what we know (or rather, very reasonably assume) about how the parent’s future statements are probabilistically related to the underlying facts about their kids.
I hope you’ve gained more appreciation for the power and subtlety of Bayesian epistemology by solving and analyzing these simple-looking puzzles.
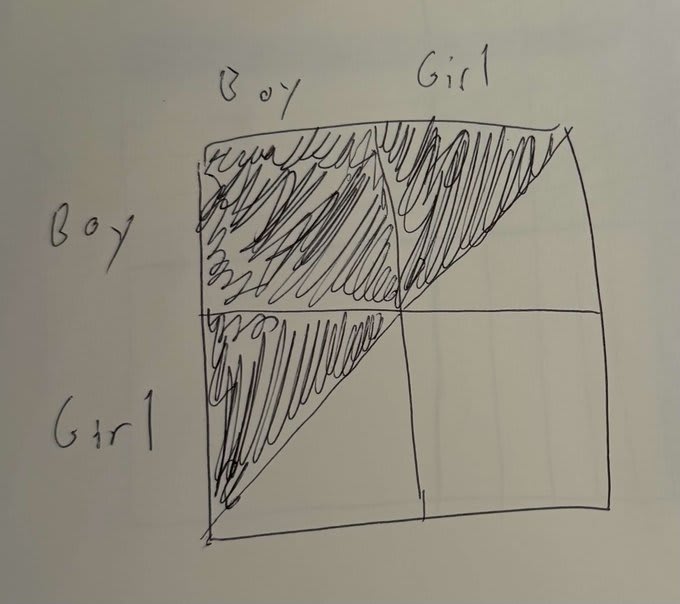
Consider two realistic scenarios:
A) I’m talking to someone and they tell me they have two children. “Oh, do you have any boys?” I ask, “I love boys!”. They nod.
B) I’m talking to someone and they tell me they have two children. One of the children then runs up to the parent. It’s a boy.
The chance of two boys is clearly 1⁄3 in the first scenario, and a half in the second.
The scenario in the question as asked is almost impossible to answer. Nobody would ever state “I have two children, at least one of whom is a boy.” in real life, so there’s no way to update in that situation. We have no way to generate good priors. Instead people make up a scenario that sounds similar but is more realistic, and because everyone does that differently they’ll all have different answers.
In scenario B, where a random child runs up, I wonder if a non-Bayesian might prefer that you just eliminate (girl, girl) and say that the probability of two boys is 1/3?
In Puzzle 1 in my post, the non-Bayesian has an interpretation that’s still plausibly reasonable, but in your scenario B it seems like they’d be clowning themselves to take that approach.
So I think we’re on the same page that whenever things get real/practical/bigger-picture, then you gotta be Bayesian.
I don’t really see how? A frequentist would just run this a few times and see that the outcome is 1⁄2.
In practice, for obvious reasons, frequentists and bayesians always agree on the probability of anything that can be measured experimentally. I think the disagreements are more philosophical about when it’s appropriate to apply probability to something at all, though I can hardly claim to be an expert in non-bayesian epistemology.
I agree that frequentists are flexible about their approach to try to get the right answer. But I think your version of the problem highlights how flexible they have to be i.e. mental gymnastics, compared to just explicitly being Bayesian all along.
The first two puzzles got some discussion on LW long ago here, and a bit more here.
One has to consider the data-generating process behind puzzles such as these. I am going to assume throughout that it is what seems to me the simplest consistent with the statement of the problems.
Every child is independently equally likely to be a boy or a girl.
Every birth day of the week is equally and independently likely.
The puzzle narrator is chosen equally at random from all members of the population for which the statements that the narrator makes are true.
One can imagine all manner of other data-generating processes, which in general will give different answers. Most quibbles with such problems come down to imagining different processes, especially for statement 3. Some examples are in the OP and the comments. However, the above assumptions seem the simplest, and the ones intended by people posing such problems. If this question came up on an exam, I would be sure to begin my answer with the above preamble.
Puzzles 1 and 2 can be unified by considering a common generalisation to there being N days in a week, one of which is called Tuesday. Puzzle 1 has N=1. Puzzle 2 has N=7.
When two children are born, there are 4 N^2 possibilities for their sexes and birthdays. Which of these are left after being given the information in the puzzle?
The sexes must be either boy-boy, boy-girl, or girl-boy.
For boy-boy, there are 2N-1 ways that at least one is born on a Tuesday. For boy-girl, there are N ways the boy could be born on a Tuesday. For girl-boy, by symmetry also N.
So the probability of boy-boy is (2N-1)/(2N-1 + N + N) = (2N-1)/(4N-1).
For N=1 this is 1⁄3, which is the generally accepted answer to Puzzle 1.
For N=7, it is 13⁄27. In general, the larger N is, the closer the probability of the other being a boy is to 1⁄2.
For Puzzle 3, the obvious answer is that before learning the day, it’s as Puzzle 1, 1⁄3, and after, it’s as Puzzle 2, 13⁄27. Is obvious answer correct answer? I have (before reading the OP’s solution) not found a reason not to think so. The OP says, by a different intuitive argument, that the obvious answer is 1⁄3, and that obvious answer is correct answer, but WilliamKiely’s comment raises a doubt, finding ambiguity in the statement of the data-generating process. This leaves me as yet undecided.
I started thinking about the ways that extra information (beyond “I have two children, at least one of whom is a boy”) affects the probability of two boys, and came up with these:
Puzzle 4. I have two children, of whom at least one is a boy with black hair. In this fictional puzzle, everyone knows that all the children in a family have the same hair colour. What is the probability that the other is also a boy?
Puzzle 5. I have two children, of whom at least one is a boy born on a Tuesday. In this fictional puzzle, everyone knows that two consecutive children never have the same birth day. What is the probability that the other is also a boy?
Puzzle 6. I have two children. The elder one is a boy. What is the probability that the younger is also a boy?
Puzzle 7. I have two children, called Alex and Sam. (In this fictional puzzle, these names communicate no information about gender.) Alex is a boy. What is the probability that Sam is a boy?
Puzzle 8. I have two children, of whom at least one is a boy. What is the probability that the elder child is a boy?
I believe the answers to these are 4: 1⁄3. 5: 6⁄13 (slightly smaller than the 13⁄27 of Puzzle 2). 6: 1⁄2. 7: 1⁄2. 8: 2⁄3. All of these can be found by the same method of considering all the possibilities that are consistent with all the information given, and counting the proportion where both children are boys.
But there is also a general idea underlying them. When you are given extra information about the boy that is said to exist, that will push the probability of the other being a boy towards 1⁄2, to the extent that the extra information breaks the symmetry between them.
In Puzzle 1, no extra information is given, and the answer is 1⁄3. In Puzzle 4, the extra information does not break the symmetry, so the probability remains 1⁄3. In Puzzles 2 and 5, it partly breaks the symmetry, and the answers lie between 1⁄3 and 1⁄2. In 6 and 7, it completely breaks the symmetry, and the answer is 1⁄2.
Puzzle 8 is Puzzle 1 with a different question, equivalent to: what is the expected proportion of boys among my children?
Puzzle 7a. I have two children, of whom at least one is a boy. Their names are Alex and Sam. (In this fictional puzzle, these names communicate no information about gender.) Alex is a boy. What is the probability that Sam is a boy?
Puzzle 1a. I have two children, of whom at least one is a boy. Now I shall toss a coin and accordingly choose one of the two children. (Does so.) The child I chose is a boy. What is the probability that the other is a boy?
“[A] boy born on a day that I’ll tell you in 5 minutes” is ambiguous. There are two possible meanings, yielding different answers.
If “a boy born on a day that I’ll tell you in 5 minutes” means “a boy, and I’ll tell you the name of a boy I have in 5 minutes” then the answer is 1⁄3 as Liron says.
However, if “a boy born on a day that I’ll tell you in 5 minutes” means “a boy born on a particular singular day that I just wrote down on this piece of paper and will show you in 5 minutes”, then this is equivalent to saying “a boy born on a Tuesday” and the answer is 13⁄27.
The reason why the second meaning is equivalent to “a boy born on a Tuesday” is because it’s a statement that at least one of the children is a particular kind of boy that only 1/7th of boys are, just like how “a boy born on a Tuesday” is a statement that at least one of the children is a particular kind of boy that only 1/7th of boys are. (Conversely, for the first interpretation: “a boy born on a day that I’ll tell you in 5 minutes” is a statement that at least one of the children is a a boy, period.)
Another way to notice the difference if it’s still not clear:
When told “I have two children, at least one of whom is [a boy born on a particular singular day that I just wrote down on this piece of paper and will show you in 5 minutes]”, you assign a 1/7th credence to the paper showing Sunday, 1/7th to Monday, 1/7th to Tuesday, etc.
Then, conditional on the paper showing Tuesday, you know that the parent just told you “I have two children, at least one of whom is [a boy born on [Tuesday and I will show you the paper showing Tuesday in 5 minutes]]”, which is equivalent to the parent saying “I have two children, at least one of whom is a boy born on Tuesday”.
So you then have a 1/7th credence that the paper shows Tuesday, and if it’s Tuesday, your credence that both children are boys is 13⁄27. So your overall credence, reflecting your uncertainty about what day the paper shows is (13/27)*(1/7)+(13/27)*(1/7)+(13/27)*(1/7)+(13/27)*(1/7)+(13/27)*(1/7)+(13/27)*(1/7)+(13/27)*(1/7)=13/27.
Could how you update your priors be dependent on what concepts you choose to represent the situation with?
I mean, suppose the parent says “I have two children, at least one of whom is a boy. So, I have a boy and another child whose gender I’m not mentioning”. It seems like that second sentence doesn’t add any new information- it parses to me like just a rephrasing of the first sentence. But now you’ve been presented with two seemingly incompatible ways of conceptualizing the scenario- either as two children of unknown gender, of whom one is a boy (suggesting a 2⁄3 chance of both being boys), or as one boy and one child of unknown gender (suggesting a 1⁄2 chance of both being boys). Having been prompted which both models, which should you choose?
It seems like one ought to have more predictive power than the other, and therefore ought to be chosen regardless of exactly how the parent phrases the statement. But it’s hard to think of a way to determine which would be more predictive in practice. If I were to select all of the pairs of two siblings in the world, discard the pairs of sisters, choose one at random and ask you to bet on whether they were both boys, you’d be wise to bet at 2⁄3 odds. But if I were to select all of the brothers with one sibling in the world and choose one along with their sibling at random, you’d want to bet at 1⁄2 odds. In the scenario above, are the unknown factors determining whether both children are boys more like that first randomization process, or more like the second? Or, maybe we have so little information about the process generating the statement that we really have no basis for deciding which is more predictive, and should just choose the simpler model?
There is also a quantum version of that puzzle.
For fermions, that probability is zero, of course. Pauli exclusion principle.
For bosons, …
… the key insight is that you can not distinguish them. The possible wave functions are either (spin-up, spin-up) or (spin-up,spin-down)=(spin-down,spin-up). Hence, you get p=1/2. (From this, we can conclude that boys (p=1/3) are made up from 2⁄3 bosons and 1⁄3 fermions.)
Why is this the most common assumption? This never made much sense to me whenever I’ve encountered this problem.
It’s much more intuitive to think about the scenario as:
2xB
1xB 1xG
2xG
Rather than:
BB
BG
GB
GG
And to come to an answer of 1⁄2 instead of 1⁄3. The question doesn’t state anything about the children’s gender being related to the order they were born.
By your logic, if I ask you a totally separate question “What’s the probability that a parent’s two kids are both boys”, would you answer 1/3? Becuase the correct answer should be 1⁄4 right? So something about your preferred methodology isn’t robust.
Good point.
You’ve made me realize that I’ve misrepresented how my intuitive mind processes this. After thinking about it a bit, a better way to write it would be:
Child 1: P(B) = 1⁄2, P(G) = 1⁄2
Child 2: P(B) = 1⁄2, P(G) = 1⁄2
Combined as unordered set {Child 1, Child 2}
The core distinction seems to be to be if you considered it an unordered set or an ordered one. I’m unsure of any way to represent that in easy to read text format, the form written above is best I’ve got.