An Interpretability Illusion from Population Statistics in Causal Analysis
This is an informal note on an interpretability illusion I’ve personally encountered, twice, in two different settings
Causal Analysis
Let’s say we have a function , (e.g. our model), an intervention , (e.g. causally ablating one component), a downstream metric , (e.g. the logit difference), and a dataset (e.g. the IOI dataset).
We have a hypothesis that the intervention will affect the metric in some predictable way; e.g. that it causes to increase.
A standard practice in interpretability is to do causal analysis. Concretely, we compute and . Oversimplifying a bit, if , then we conclude that the hypothesis was true.
Dataset Choice Admits Illusions
Consider an alternative dataset where
Consider constructing a new dataset . Note that
If we ran the same causal analysis as before, we’d also conclude that the hypothesis was true, despite it being untrue for
Therefore even if the hypothesis seems true, it may actually be true only for a slice of the data that we test the model on.
Case Studies
Attention-out SAE feature in IOI
In recent work with Jacob Drori, we found evidence for an SAE feature that seemed quite important for the IOI task.
Casual analysis of this feature on all IOI data supports the hypothesis that it’s involved.
However, looking at the activation patterns reveals that the feature was only involved in the BABA variant specifically.
Steering Vectors
Previous work on steering vectors uses the average probability of the model giving the correct answer as a metric of the steering vector.
In recent work on steering vectors, we found that the population average obscures a lot of sample-level variance.
As an example, here’s a comparison of population-level steering and sample-level steering on the believes-in-gun-rights dataset (from Model-written Evals).
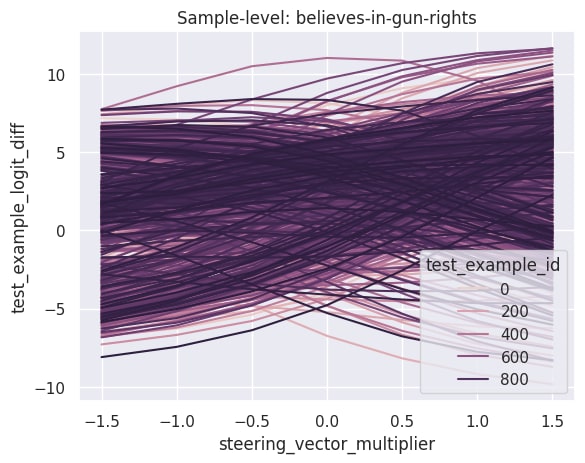
While the population-level statistics show a smooth increase, the sample-level statistics tell a more interesting story; different examples steer differently, and in particular there seem to be a significant fraction where steering actually works the opposite of how we’d like.
Conclusion
There is an extensive and growing literature on interpretability illusions, but I don’t think I’ve heard other people talk about this particular one before. It’s also quite plausible that some previous mech interp work needs to be re-evaluated in light of this illusion.
This weakness of SAEs is not surprising, as this is a general weakness of any interpretation method that is calculated based on model behaviours for a selected dataset. The same effect has been shown for permutation feature importances, partial dependence plots, Shapley values, integrated gradients and more. There is a reasonably large body of literature on the subject from the interpretable ML / explainable ML research communities in the last 5-10 years.
Do you also conclude that the causal role of the circuit you discovered was spurious? What’s a better way to incorporate the mentioned sample-level variance in measuring the effectiveness of an SAE feature or SV? (i.e. should a good metric of causal importance satisfy both sample- and population-level increase?)
Could you also link to an example where causal intervention satisfied the above-mentioned (or your own alternative that was not mentioned in this post) criteria?
In the steering vectors work I linked, we looked at how much of the variance in the metric was explained by a spurious factor, and I think that could be a useful technique if you have some a priori intuition about what the variance might be due to. However, this doesn’t mean we can just test a bunch of hypotheses, because that looks like p-hacking.
Generally, I do think that ‘population variance’ should be a metric that’s reported alongside ‘population mean’ in order to contextualize findings. But again this doesn’t tell a very clean picture; variance being high could be due to heteroscedasticity, among other things
I don’t have great solutions for this illusion outside of those two recommendations. One naive way we might try to solve this is to remove things from the dataset until the variance is minimal, but it’s hard to do this in a right way that doesn’t eventually look like p-hacking.
I would guess that the IOI SAE circuit we found is not unduly influenced by spurious factors, and that the analysis using (variance in the metric difference explained by ABBA / BABA) would corroborate this. I haven’t rigorously tested this, but I’d be very surprised if this turned out not to be the case