A Case for Cooperation: Dependence in the Prisoner's Dilemma

“The man who is cheerful and merry has always a good reason for being so,—the fact, namely, that he is so.” The Wisdom of Life, Schopenhauer (1851)

TL;DR

Descriptions of the Prisoner’s Dilemma typically suggest that the optimal policy for each prisoner is to selfishly defect instead of to cooperate. I disagree with the traditional analysis and present a case for cooperation.

The core issue is the assumption of independence between the players. Articulations of the game painstakingly describe how the prisoners are in explicitly separate cells with no possibility of communication. From this, it’s assumed that one’s action can have no causal effect on the decision of the other player. However, (almost) everything is correlated, and this significantly changes the analysis.

Imagine the case where the prisoners are clones and make exactly the same decision. Then, when they compare the expected payout for each possible action, their payout will be higher in the case where they cooperate because they are certain the other player is having the same thoughts and deterministically will make the same choice. This essay generalizes and formalizes this line of reasoning.

Here’s what to expect in what follows. In the first section, we begin by introducing the standard causal decision theory analysis suggesting (Defect, Defect). Then, we introduce the machinery for mixed strategies in the following section. From there we discuss the particular case where both participants are clones, which motivates our new framework. Then, we introduce a bit more formalism around causal modeling and dependence. We proceed to analyze a more general case where both players converge to the same mixed strategy. Then we discuss the most general model, where the players’ mixed strategies have some known correlation. Finally, we conclude the analysis. In summary, given some dependency structure due to upstream causal variables, we uncover the cases where the game theory actually suggests cooperation as the optimal policy.

The Traditional Analysis

In Game Theory 101, here’s how the Prisoner’s Dilemma analysis traditionally goes. Alice and Bob are conspirators in a crime. They’re both caught and brought to separate interrogation rooms. They’re presented with a Faustian bargain: to snitch or not to snitch. If neither snitches on the other, they both get a 1-year sentence. If one snitches and the other does not, then the snitch goes home free while the non-snitch has to serve 3 years. If they both snitch, they serve 2 years.

Here’s the payoff diagram corresponding with this setup:

$\begin{matrix} B_{C} & B_{D} A_{C} & (- 1, - 1) & (- 3, 0) A_{D} & (0, - 3) & (- 2, - 2) \end{matrix}$

If Alice cooperates, Bob is better off defecting to get 0 years instead of 1 year. If Alice defects, Bob is better off defecting to get 2 years instead of 3 years. So in either case Bob is better off defecting. A strategy which is optimal regardless of the choices of an opponent is called a dominant strategy. Symmetrically, Alice is better off defecting no matter what Bob does. This means that even though they’re both happier in the case where they both cooperate, serving just one year each, the “Nash equilibrium” is the case where they both defect, serving two years each. A state is called a Nash equilibrium if no player can benefit by changing their action, holding the actions of all other players constant.

We can represent each player’s preferences and optimal choices with an arrow diagram.

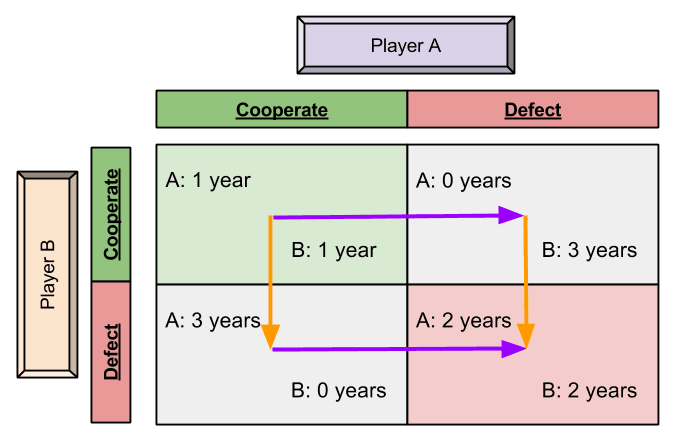
Nash equilibria are represented by a state with no arrows pointing away from it, meaning no player would prefer to switch their choice, holding the other players’ choices the same. In the example above, (Defect, Defect) is the single Nash equilibrium.

We can generalize the payoff matrix a bit to represent all situations that capture the structure of a “Prisoner’s Dilemma”-like scenario.

$\begin{matrix} B_{C} & B_{D} A_{C} & (R, R) & (S, T) A_{D} & (T, S) & (Q, Q) \end{matrix}$

I use the variables $Q, R, S, T$ to keep organized. These can be remembered in the following way. $Q$ is the $Q$ uarrel payout when they rat each other out. $R$ is the $R$ eward for mutual cooperation. $S$ is the $S$ ucker’s payout if the other player snitches and they do not. $T$ is the $T$ emptation payout for snitching while the other does not. The necessary and sufficient conditions for a prisoner’s dilemma structure are that $S < Q < R < T$ .

Probabilistic Play

Now, let’s make our model a bit more rigorous and extend our binary action space to a probabilistic strategy model.

$\begin{matrix} B_{C} & B_{D} A_{C} & (R, R) & (S, T) A_{D} & (T, S) & (Q, Q) \end{matrix}$

Instead of discrete actions, let’s suppose Alice and Bob each choose mixed strategy vectors $[p (A_{c}), p (A_{d})]$ and $[p (B_{c}), p (B_{d})]$ , respectively, which represent their probabilities of cooperation or defection, such that $p (A_{c}) + p (A_{d}) = 1$ and $p (B_{c}) + p (B_{d}) = 1$ .

We formalize the analysis by noting that Alice wants to maximize her expected (VNM) utility. We now compute her optimal cooperation fraction $p^{*} (A_{c} | B^{*})$ given Bob’s optimal policy.

$E [U_{A} (G)] = E [U_{A} (G | A_{c})] p^{*} (A_{c}) + E [U_{A} (G | A_{d})] p^{*} (A_{d})$

We decompose the expected value of the game to Alice $E [U_{A} (G)]$ into the expected value of the game given that she cooperates $E [U_{A} (G | A_{c})]$ times the probability that she cooperates $p^{*} (A_{c})$ plus the expected value of the game given that she defects $E [U_{A} (G | A_{d})]$ times the probability she defects $p^{*} (A_{d})$ .

We can further clarify Alice’s expected utility given her action $E [U_{A} (G | A_{c})]$ into the cases where Bob cooperates and does not cooperate.

$E [U_{A} (G | A_{c})] = E [U_{A} (G | A_{c}, B_{c})] p^{*} (B_{c}) + E [U_{A} (G | A_{c}, B_{d})] p^{*} (B_{d})$

$E [U_{A} (G | A_{d})] = E [U_{A} (G | A_{d}, B_{c})] p^{*} (B_{c}) + E [U_{A} (G | A_{d}, B_{d})] p^{*} (B_{d})$

Bringing this back into our equation for $E [U_{A} (G)]$ yields:

$\begin{matrix} E [U_{A} (G)] = E [U_{A} (G | A_{c}, B_{c})] p^{*} (A_{c}) p^{*} (B_{c}) + E [U_{A} (G | A_{c}, B_{d})] p^{*} (A_{c}) p^{*} (B_{d}) + E [U_{A} (G | A_{d}, B_{c})] p^{*} (A_{d}) p^{*} (B_{c}) + E [U_{A} (G | A_{d}, B_{d})] p^{*} (A_{d}) p^{*} (B_{d}) \end{matrix}$

We can reduce the mess a bit by substituting in our variables $Q, R, S, T$ .

$\begin{matrix} E [U_{A} (G)] = R p^{*} (A_{c}) p^{*} (B_{c}) + S p^{*} (A_{c}) p^{*} (B_{d}) + T p^{*} (A_{d}) p^{*} (B_{c}) + Q p^{*} (A_{d}) p^{*} (B_{d}) \end{matrix}$

Now we apply $p (A_{c}) + p (A_{d}) = 1$ and $p (B_{c}) + p (B_{d}) = 1$ .

$\begin{matrix} E [U_{A} (G)] = R p^{*} (A_{c}) p^{*} (B_{c}) + S p^{*} (A_{c}) (1 - p^{*} (B_{c})) + T (1 - p^{*} (A_{c})) p^{*} (B_{c}) + Q (1 - p^{*} (A_{c})) (1 - p^{*} (B_{c})) \end{matrix}$

Normally to find the $p^{*} (A_{c})$ which maximizes $E [U_{A} (G)]$ we would differentiate $E [U_{A} (G)]$ with respect to $p^{*} (A_{c})$ and set this result to zero. But because the equation is linear in $p^{*} (A_{c})$ , the derivative degenerates. This means that there won’t be an optimal “mixed strategy” which is not a “pure strategy”, meaning that given the prisoner’s dilemma payout structure presented thus far Alice and Bob are better off making a decision to 100% cooperate or 100% defect.

Expanding out $E [U_{A} (G)]$ a bit further we see:

$\begin{matrix} E [U_{A} (G)] = R p^{*} (A_{c}) p^{*} (B_{c}) + S p^{*} (A_{c}) - S p^{*} (A_{c}) p^{*} (B_{c}) + T p^{*} (B_{c}) - T p^{*} (B_{c}) p^{*} (A_{c}) + Q - Q p^{*} (A_{c}) - Q p^{*} (B_{c}) + Q p^{*} (A_{c}) p^{*} (B_{c}) \end{matrix}$

Now we isolate $p^{*} (A_{c})$ :

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{c}) [R p^{*} (B_{c}) + S - S p^{*} (B_{c}) - T p^{*} (B_{c}) - Q + Q p^{*} (B_{c})] + [T p^{*} (B_{c}) + Q - Q p^{*} (B_{c})] \end{matrix}$

$E [U_{A} (G)] = p^{*} (A_{c}) [p^{*} (B_{c}) (Q + R - S - T) + (S - Q)] + [p^{*} (B_{c}) (T - Q) + Q]$

To see if Alice’s optimal cooperation percentage $p^{*} (A_{c})$ is 100% or 0%, we just need to see if the term $p^{*} (B_{c}) (Q + R - S - T) + (S - Q)$ is greater than or less than zero. If it’s greater than zero, then Alice best maximizes $E [U_{A} (G)]$ when $p^{*} (A_{c}) = 1$ , and correspondingly when it’s less than zero then Alice should always defect ( $p^{*} (A_{c}) = 0$ ).

$R p^{*} (B_{c}) + S - S p^{*} (B_{c}) - T p^{*} (B_{c}) - Q + Q p^{*} (B_{c}) ? < 0$

$0 ? < (T p^{*} (B_{c}) - R p^{*} (B_{c})) + (S p^{*} (B_{c}) - S) + (Q - Q p^{*} (B_{c}))$

$0 ? < p^{*} (B_{c}) (T - R) + Q (1 - p^{*} (B_{c})) - S (1 - p^{*} (B_{c}))$

$0 ? < p^{*} (B_{c}) (T - R) + (1 - p^{*} (B_{c})) (Q - S)$

We now show that each piece is greater than zero. $p^{*} (B_{c}) > 0$ , $T - R > 0$ because $T > R$ , $1 - p^{*} (B_{c}) > 0$ , and $Q - S > 0$ because $Q > S$ . Therefore, $0 > p^{*} (B_{c}) (T - R) + (1 - p^{*} (B_{c})) (Q - S)$ , and Alice’s optimal policy is to always defect. The same analysis can be performed for Bob as well.

This is how the analysis typically goes. The common perspective is that, given the payoff diagram and the constraint that $T > R > Q > S$ , in a two-player simultaneous game where the players cannot communicate with one another, then unfortunately the game theory optimal policy is always to defect.

$\begin{matrix} B_{C} & B_{D} A_{C} & (R, R) & (S, T) A_{D} & (T, S) & (Q, Q) \end{matrix}$

I disagree with this conclusion and present my own analysis in the subsequent section.

The Clone Case for Cooperation

In the typical analysis of the prisoner’s dilemma, we consider the choices of Alice and Bob to be independent of each other. This is because they make their decisions simultaneously and have no way of affecting the decision of the other. But, there is an underlying dependence structure between A and B that we must include in our model.

To illustrate this, imagine the case where Alice is cloned and given exactly the same environment such that both clones will make the same decisions. If we label clone A and clone B, in this case we now have $p (B_{C} | A_{C}) = 1$ , implying $p (B_{D} | A_{C}) = 0$ , $p (B_{D} | A_{D}) = 1$ , and $p (B_{C} | A_{D}) = 0$ . This is the case where there’s perfect correlation between the decisions of A and B, which we analyze in this section.

Let’s now recompute A’s expected utility $E [U_{A} (G)]$ which she wants to maximize.

$E [U_{A} (G)] = E [U_{A} (G | A_{C})] p^{*} (A_{C}) + E [U_{A} (G | A_{D})] p^{*} (A_{D})$

Variable definitions:

$E [U_{A} (G)]$ is the expected utility of the game to player A.
$E [U_{A} (G | A_{C})]$ is the expected utility of the game to player A given that A choses to cooperate.
$E [U_{A} (G | A_{D})]$ is the expected utility of the game to player A given that A choses to defect.
$p^{*} (A_{C})$ is the probability that A cooperates, which is optimized to maximize A’s expected utility given her knowledge.
$p^{*} (A_{D})$ is the probability that A defects, which is optimized to maximize A’s expected utility given her knowledge.

Given B’s potentially mixed strategy, the expected utility of the game to A given each of A’s possible choices can be decomposed into the cases for each of B’s choices given A’s choice.

$E [U_{A} (G | A_{C})] = E [U_{A} (G | A_{C}, B_{C})] {^p}_{A} (B_{C} | A_{C}) + E [U_{A} (G | A_{C}, B_{D})] {^p}_{A} (B_{D} | A_{C})$

$E [U_{A} (G | A_{D})] = E [U_{A} (G | A_{D}, B_{C})] {^p}_{A} (B_{C} | A_{D}) + E [U_{A} (G | A_{D}, B_{D})] {^p}_{A} (B_{D} | A_{D})$

Notice that we condition B’s probabilities on A’s choice. In the previous analysis, we claimed that B has no way of seeing A’s choice so we make them independent, claiming $p (B_{C} | A_{C}) = p (B_{C})$ . But this is NOT RIGHT. Also, notice we place a hat on ${^p}_{A} (B_{x} | A_{y})$ to denote that these are A’s estimates of B’s action probabilities based on A’s own knowledge. We will come back to discuss this step in more detail in a later section, but note that this is the heart of the difference between my perspective and the traditional analysis.
Academic economists would likely claim (have claimed) that this approach doesn’t sufficiently separate belief formation and decision making. The type of recursive relationship I’m suggesting between estimating a counterparties’ policy and our own action selection seems “irrational”, in the sense that it doesn’t follow the typical pre-defined “rational decision making” algorithm described by economists. However, I point out that the policy presented here wins at games. That is, it is the policy which results in both agents obtaining maximum expected utility.
It’s been recommended by an econ friend (who I love dearly), that while this approach might not fit the classification of “rational decision making”, it could find a home in the behavioral economics literature as a form of *motivated reasoning*. The claim is that the agent wants to maximize their ex-ante expected utility and this model assumes their beliefs are malleable. A motivated reasoner wants to believe their counterparty to act as they do, so they “trick” themselves into believing it even though they haven’t rationally deduced that the counterparty will actually cooperate. The academic argument against cooperation continues, “but this cannot be fully rational behavior, because my ex-post decision has to be fully independent from the other agent, as my decision, because it is unknown to them at the time of their own decision by construction, cannot influence their beliefs and so should not influence my own beliefs about their action.” It’s this notion that decisions are made independently that I take issue with. I discuss this further in the Everything is Correlated section which follows.

We now recombine this into $E [U_{A} (G)]$ :

$\begin{matrix} E [U_{A} (G)] = (E [U_{A} (G | A_{C}, B_{C})] {^p}_{A} (B_{C} | A_{C}) + E [U_{A} (G | A_{C}, B_{D})] {^p}_{A} (B_{D} | A_{C})) p^{*} (A_{C}) + (E [U_{A} (G | A_{D}, B_{C})] {^p}_{A} (B_{C} | A_{D}) + E [U_{A} (G | A_{D}, B_{D})] {^p}_{A} (B_{D} | A_{D})) p^{*} (A_{D}) \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = E [U_{A} (G | A_{C}, B_{C})] {^p}_{A} (B_{C} | A_{C}) p^{*} (A_{C}) + E [U_{A} (G | A_{C}, B_{D})] {^p}_{A} (B_{D} | A_{C}) p^{*} (A_{C}) + E [U_{A} (G | A_{D}, B_{C})] {^p}_{A} (B_{C} | A_{D}) p^{*} (A_{D}) + E [U_{A} (G | A_{D}, B_{D})] {^p}_{A} (B_{D} | A_{D}) p^{*} (A_{D}) \end{matrix}$

Now we substitute in $Q, R, S, T$ and use $p^{*} (A_{C}) + p^{*} (A_{D}) = 1$ and ${^p}_{A} (B_{C} | A_{x}) + {^p}_{A} (B_{D} | A_{x}) = 1$ .

$\begin{matrix} E [U_{A} (G)] = {^p}_{A} (B_{C} | A_{C}) p^{*} (A_{C}) R + (1 - {^p}_{A} (B_{C} | A_{C})) p^{*} (A_{C}) S + {^p}_{A} (B_{C} | A_{D}) (1 - p^{*} (A_{C})) T + (1 - {^p}_{A} (B_{C} | A_{D})) (1 - p^{*} (A_{C})) Q \end{matrix}$

Notice that, if the choices of the players are truly independent, then ${^p}_{A} (B_{x} | A_{y}) = {^p}_{A} (B_{x})$ , yielding the traditional analysis of the last section.

Let’s now explore the case where A and B are clones who will make exactly the same choice, so ${^p}_{A} (B_{x} | A_{x}) = 1$ and ${^p}_{A} (B_{x} | A_{\neg x}) = 0$ . Let’s now update our $E [U_{A} (G)]$ calculation.

$\begin{matrix} E [U_{A} (G)] = 1 p^{*} (A_{C}) R + (1 - 1) p^{*} (A_{C}) S + 0 (1 - p^{*} (A_{C})) T + (1 - 0) (1 - p^{*} (A_{C})) Q \end{matrix}$

Which we simplify into:

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{C}) R + (1 - p^{*} (A_{C})) Q \end{matrix}$

$E [U_{A} (G)] = p^{*} (A_{C}) R + Q - Q p^{*} (A_{C})$

$E [U_{A} (G)] = p^{*} (A_{C}) (R - Q) + Q$

Because $R$ eward $>$ $Q$ uarrel, $E [U_{A} (G)]$ is maximized when $p^{*} (A_{C}) = 1$ ! This means $A$ will cooperate and receive $E [U_{A} (G)] = R$ eward instead of $Q$ uarrel, and similarly for $B$ . This seems trivial, but if $A$ and $B$ can make the same decision, they can obtain the globally optimal solution instead of the strictly worse typical Nash equilibrium which is reached when they believe they act independently.

Everything is Correlated

Alright, if Alice knows that Bob will make exactly the same decision, she can fearlessly cooperate, knowing for certain that he will too, dissolving the dilemma. So now, let’s reincorporate uncertainty back into our model.

Let’s say Alice and Bob are not clones but are instead siblings with similar family values, experiences, dispositions, genes, neurological structures, etc. We know that many, many, many things in the world are correlated in some way. The dependency structure of the world is extremely interconnected. There’s also an evolutionary argument for this that I won’t get to in much detail. But when picking the prisoners, we’re actually sampling players who have played an iterated version of this game many many times. If you believe that humans are not purely rational agents and make decisions based on instinct, then there’s likely to be downstream similarity in their policies. And if you believe that the agents are purely rational, they also have exactly the same game-theoretic payouts, so their GTO play should be exactly the same. It would be extremely improbable for Alice and Bob’s choices here to be perfectly independent. So let’s model some dependence structure.

(I will note that there’s a semi-compelling argument suggesting that we don’t even need to introduce more subtle forms of dependence. Because they have identical payoff structures, the game-theoretic optimal play should be exactly the same. Given their GTO play should be exactly the same and mixed strategies degenerate to pure strategies, we get correlation 1, and so they should both coordinate 100% of the time. But the real world is messy, so we proceed with slightly more subtlety.)

Causal Modeling 101

To better understand the dependencies and correlations between Alice and Bob’s choices, we can frame the problem in the light of causal modeling a la Judea Pearl. In causal modeling, we represent the dependencies between variables using a directed acyclic graph (DAG), where nodes represent variables and directed edges represent causal relationships.

In the traditional analysis of the Prisoner’s Dilemma, Alice and Bob are assumed to make their decisions independently. However, in reality, their decisions will definitely be influenced by common upstream factors. For example, Alice and Bob may have similar upbringings, values, experiences, and expectations about loyalty and cooperation that influence their decision-making. And if that’s not compelling, they also have access to similar information about the situation, and have exactly the same payout structure, so there’s a strong case that they will end up making similar decisions.

We can represent these upstream factors with a variable $V$ . The causal model can be depicted as follows:

  V
 / \
A   B

Here, $V$ is a common cause that affects both Alice’s and Bob’s decisions. This creates a dependency between $A$ and $B$ .

Given the upstream factor $V$ , the choices of Alice and Bob could be conditionally independent. However, if we do not observe $V$ , the choices $A$ and $B$ become dependent. This is known as d-separation in causal graphs.

Mathematically, this can be expressed as:

$P (A, B) = \sum_{v} P (A ∣ V = v) P (B ∣ V = v) P (V = v)$

This shows that the joint probability of $A$ and $B$ depends on their conditional probabilities given $V$ and the distribution of $V$ .

Independent Case (Optional)

Suppose A and B were truly independent. Here’s the causal model we might associate with this hypothesis.

 V_1     V_2
  |       |
  A       B

Here $V_{1}$ and $V_{2}$ are separate upstream factors that affect Alice’s and Bob’s decisions, respectively. This creates a scenario where $A$ and $B$ are conditionally independent given $V_{1}$ and $V_{2}$ . Mathematically, this can be expressed as:

$P (A, B) = \sum_{v_{1}} \sum_{v_{2}} P (A ∣ V_{1} = v_{1}) P (B ∣ V_{2} = v_{2}) P (V_{1} = v_{1}) P (V_{2} = v_{2})$

This equation shows that the joint probability of $A$ and $B$ depends on their individual probabilities given $V_{1}$ and $V_{2}$ , and the distribution of $V_{1}$ and $V_{2}$ .

To prove the typical independence equation $P (A, B) = P (A) P (B)$ from the more complicated seeming equation above, we first find the marginal probabilities $P (A)$ and $P (B)$ and sum over the respective upstream variables:

$P (A) = \sum_{v_{1}} P (A ∣ V_{1} = v_{1}) P (V_{1} = v_{1})$

$P (B) = \sum_{v_{2}} P (B ∣ V_{2} = v_{2}) P (V_{2} = v_{2})$

Now we multiply $P (A)$ and $P (B)$ together:

$P (A) P (B) = (\sum_{v_{1}} P (A ∣ V_{1} = v_{1}) P (V_{1} = v_{1})) (\sum_{v_{2}} P (B ∣ V_{2} = v_{2}) P (V_{2} = v_{2}))$

Then we expand the product of the sums and we notice that this expression is the same as the expression for the joint probability $P (A, B)$ obtained in step 1:

$P (A) P (B) = \sum_{v_{1}} \sum_{v_{2}} P (A ∣ V_{1} = v_{1}) P (V_{1} = v_{1}) P (B ∣ V_{2} = v_{2}) P (V_{2} = v_{2})$
Because the two expressions are identical, we’ve shown that $P (A, B) = P (A) P (B)$ assuming that Alice’s and Bob’s decisions are influenced by separate, independent upstream variables $V_{1}$ and $V_{2}$ . With this extra machinery in hand, we proceed into the heart of our analysis.

Incorporating Dependence into Expected Utility

In The Clone Case for Cooperation section, I make the assumption that Alice and Bob deterministically make exactly the same choice. This time, let’s relax that assumption and suppose that because they’re rational agents presented with identical payoff matrices, they’ll conclude the same mixed strategies to be optimal. Though we’re not sure what their cooperate/defect probabilities will be yet, we just suppose that their GTO policies will be the same given the same payout structures.

To model this formulation, we go back to the start and split A’s expected utility based on her two possible actions.

$E [U_{A} (G)] = E [U_{A} (G | A_{C})] p^{*} (A_{C}) + E [U_{A} (G | A_{D})] p^{*} (A_{D})$

Then, we split each of those cases for each of B’s possible choices.

Now we substitue in $Q, R, S, T$ and use $p^{*} (A_{C}) + p^{*} (A_{D}) = 1$ and ${^p}_{A} (B_{C} | A_{x}) + {^p}_{A} (B_{D} | A_{x}) = 1$ .

Now we need thoughtful ways of modeling ${^p}_{A} (B_{C} | A_{C})$ and ${^p}_{A} (B_{C} | A_{D})$ . For Alice’s approximation of Bob’s probability of collaborating, ${^p}_{A} (B_{C} | A_{C})$ , we can suppose that this matches Alice’s own probability of collaborating $p^{*} (A_{C})$ because of our assumption that rational agents will come to the same mixed strategy policies given identical payoff matrices. So, ${^p}_{A} (B_{C} | A_{C}) = p^{*} (A_{C})$ and ${^p}_{A} (B_{C} | A_{D}) = 1 - {^p}_{A} (B_{D} | A_{D}) = 1 - p^{*} (A_{D}) = p^{*} (A_{C})$ .

This turns our $E [U_{A} (G)]$ into:

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{C}) p^{*} (A_{C}) R + (1 - p^{*} (A_{C})) p^{*} (A_{C}) S + p^{*} (A_{C}) (1 - p^{*} (A_{C})) T + (1 - p^{*} (A_{C})) (1 - p^{*} (A_{C})) Q \end{matrix}$

Which simplifies to:

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{C})^{2} R + p^{*} (A_{C}) (1 - p^{*} (A_{C})) S + p^{*} (A_{C}) (1 - p^{*} (A_{C})) T + (1 - p^{*} (A_{C}))^{2} Q \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{C})^{2} R + (p^{*} (A_{C}) - p^{*} (A_{C})^{2}) S + (p^{*} (A_{C}) - p^{*} (A_{C})^{2}) T + (1 - 2 p^{*} (A_{C}) + p^{*} (A_{C})^{2}) Q \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = R p^{*} (A_{C})^{2} + S p^{*} (A_{C}) - S p^{*} (A_{C})^{2} + T p^{*} (A_{C}) - T p^{*} (A_{C})^{2} + Q - 2 Q p^{*} (A_{C}) + Q p^{*} (A_{C})^{2} \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = (R - S - T + Q) p^{*} (A_{C})^{2} + (S + T - 2 Q) p^{*} (A_{C}) + Q \end{matrix}$

Optimizing (Optional)

All that’s left to do from here is to find the $p^{*} (A_{C})$ which maximizes $E [U_{A} (G)]$ subject to the constraints that $0 \leq p^{*} (A_{C}) \leq 1$ and $S < Q < R < T$ . (The cases get slightly hairy so this section is skippable.)

Unlike the previous case where $f_{E [U_{A} (G)]} (p^{*} (A_{C}))$ was linear, this time we actually can optimize via the derivative method suggested earlier. To do so, we compute:

$\frac{d E [U_{A} (G)]}{d p^{*} (A_{C})} = 2 (Q + R - S - T) p^{*} (A_{C}) + (S + T - 2 Q) = 0$

Because $f_{E [U_{A} (G)]} (p^{*} (A_{C}))$ is a second-degree polynomial, the parabola it sweeps out will have its vertex at $p^{*} (A_{C}) = \frac{(2 Q - S - T)}{2 (Q + R - S - T)}$ . While there’s still some tidying up to do to determine which cases apply to which solutions, excitingly, the possible solution set is constrained to ${0, \frac{(2 Q - S - T)}{2 (Q + R - S - T)}, 1}$ . This vertex won’t always be the maximum, and sometimes this vertex will be outside the valid probability range $[0, 1]$ . In either of these countercases, the maximum value for $p^{*} (A_{C})$ will be either $0$ or $1$ .

We now describe the cases where the vertex is a valid maximum. For the vertex to be a maximum, the parabola must be concave. As we know, a $y = a x^{2} + b x + c$ parabola is concave when $a < 0$ . So, Q+R-S-T<0 or $Q + R < S + T$ . For the vertex to be valid, we say it must lie within the domain $0 \leq p^{*} (A_{C}) \leq 1$ . First, to find the inequalities implied by $0 \leq p^{*} (A_{C}) = \frac{(2 Q - S - T)}{2 (Q + R - S - T)}$ , we note that because the parabola is concave down, the denominator $Q + R - S - T$ will be negative, so $0 \geq 2 Q - S - T$ $⟹$ $S + T \geq 2 Q$ . Second, $p^{*} (A_{C}) = \frac{(2 Q - S - T)}{2 (Q + R - S - T)} \leq 1$ implies that $2 Q - S - T \leq 2 (Q + R - S - T)$ $⟹$ $S + T \leq 2 R$ . We’ve found that, when $Q + R < S + T$ and $2 Q \leq S + T \leq 2 R$ , then the optimal cooperation fraction for Alice will be $p^{*} (A_{C}) = \frac{1}{2} (\frac{Q - R}{Q + R - S - T}) + \frac{1}{2}$ .

We still have to sort out when $p^{*} (A_{C})$ will be $1$ or $0$ , and there’s a bit of tidying up to do when the denominator $2 (R - S - T + Q)$ is zero (which actually was the case in the first example in the Traditional Analysis section where $R = - 1$ , $S = - 3$ , $T = 0$ , and $Q = - 2$ ). To solve this indeterminate case this when $R - S - T + Q = 0$ , we take the second derivative of $E [U_{A} (G)]$ : $\frac{d^{2} E [U_{A} (G)]}{d (p^{*} (A_{C}))^{2}} = 2 (Q + R - S - T)$ . Because in this case Q+R-S-T = 0, the second derivative is zero, implying that the expected utility curve will be linear.

So, when $R - S - T + Q = 0$ , $E [U_{A} (G)] = (S + T - 2 Q) p^{*} (A_{C}) + Q$ , where here $E [U_{A} (G)]$ is a linear function of $p^{*} (A_{C})$ . In this edge case, we find that:

If $S + T - 2 Q > 0$ , $E [U_{A} (G)]$ increases with $p^{*} (A_{C})$ . Therefore, $p^{*} (A_{C}) = 1$ is optimal.
If $S + T - 2 Q < 0$ , $E [U_{A} (G)]$ decreases with $p^{*} (A_{C})$ . Therefore, $p^{*} (A_{C}) = 0$ is optimal.
If $S + T - 2 Q = 0$ , $E [U_{A} (G)]$ is constant, and any $p^{*} (A_{C})$ is optimal.

For the other cases where we’re deciding between 0 or 1, we just need to compare $f_{E [U_{A} (G)]} (p (A_{C}) = 0)$ with $f_{E [U_{A} (G)]} (p (A_{C}) = 1)$ . That is, we need to compare $(R - S - T + Q) 0^{2} + (S + T - 2 Q) 0 + Q = Q$ with $(R - S - T + Q) 1^{2} + (S + T - 2 Q) 1 + Q$ $=$ $(R - S - T + Q) + (S + T - 2 Q) + Q = R$ . That is, in these cases, if $R > Q$ then $p^{*} (A_{C}) = 1$ , and if $Q > R$ then $p^{*} (A_{C}) = 0$ .

Putting this all together:

If $Q + R < S + T$ and $2 Q \leq S + T \leq 2 R$ , then the optimal cooperation fraction for Alice will be $p^{*} (A_{C}) = \frac{1}{2} (\frac{Q - R}{Q + R - S - T}) + \frac{1}{2}$ .
If $Q + R = S + T$ then:
- If $S + T - 2 Q > 0$ , then $p^{*} (A_{C}) = 1$ .
- If $S + T - 2 Q < 0$ , then $p^{*} (A_{C}) = 0$ .
- If $S + T - 2 Q = 0$ , then any $p^{*} (A_{C})$ is optimal.
Otherwise:
- If $R < Q$ then $p^{*} (A_{C}) = 0$ .
- If $R = Q$ then $p^{*} (A_{C}) = \frac{1}{2}$ .
- If $R > Q$ then $p^{*} (A_{C}) = 1$ .

Represented as one piecewise expression:
$p^{*} (A_{C}) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} \frac{1}{2} (\frac{Q - R}{Q + R - S - T}) + \frac{1}{2} & if Q + R < S + T and 2 Q \leq S + T \leq 2 R, 0 & if Q + R = S + T and S + T - 2 Q < 0, p^{*} (A_{C}) \in [0, 1] & if Q + R = S + T and S + T - 2 Q = 0, 1 & if Q + R = S + T and S + T - 2 Q > 0, 0 & if Q + R > S + T and R < Q, \frac{1}{2} & if Q + R > S + T and R = Q, 1 & if Q + R > S + T and R > Q . \end{matrix}$

At last, if we make the assumption that A and B will conclude the same mixed strategy fractions to be optimal, given that they have identical payoffs, we now have a complete policy for determining their choices of optimal $p^{*} (A_{C})$ and $p^{*} (B_{C})$ .

Interpretation

Let’s interpret this solution a bit to make sure it accords with our intuitions. We start with the complicated seeming expression, $p^{*} (A_{C}) = \frac{1}{2} (\frac{Q - R}{Q + R - S - T}) + \frac{1}{2}$ , in the case where $Q + R < S + T$ and $2 Q \leq S + T \leq 2 R$ .

This equation indicates that the optimal cooperation probability depends on the difference between the $Q$ uarrel and $R$ eward payoffs, normalized by the overall differences between the players’ payoffs when they perform the same action minus when they perform different actions. This value should be between −1 and 1, which bounds $p^{*} (A_{C})$ between −1 and 1, as we would expect a probability to behave.

We continue to examine some important boundary conditions:

If $Q$ uarrel $= R$ eward, then $p^{*} (A_{C}) = \frac{1}{2}$ , indicating that the player is indifferent between cooperation and defection.
If $Q$ uarrel $> R$ eward, then $p^{*} (A_{C}) < \frac{1}{2}$ , indicating a higher probability of defection. (Remember the denominator is negative in this case.)
If $Q$ uarrel $< R$ eward, then $p^{*} (A_{C}) > \frac{1}{2}$ , indicating a higher probability of cooperation. (Again the denominator is negative.)

This result seems reasonable because if the quarrel payoff $Q$ is better than the reward for mutual cooperation $R$ , Alice is more likely to defect. Conversely, if $R$ is better, Alice is more likely to cooperate.

Let’s now try to apply this policy to our initial toy example. To see if our solution holds, we test the case when $R = - 1$ , $S = - 3$ , $T = 0$ , $Q = - 2$ .

$\begin{matrix} B_{C} & B_{D} A_{C} & (- 1, - 1) & (- 3, 0) A_{D} & (0, - 3) & (- 2, - 2) \end{matrix}$

First, we calculate $R - S - T + Q = - 1 - (- 3) - 0 + (- 2) = 0$ . Then, because $R - S - T + Q = 0$ , we use the indeterminate case formula. We calculate $S + T - 2 Q = - 3 + 0 - 2 (- 2) = 1$ . Finally, since, $S + T - 2 Q > 0$ , the optimal policy is $p^{*} (A_{C}) = 1$ . This aligns with the interpretation that Alice should always cooperate in this particular setup.

We can also confirm this computationally as well.

import matplotlib.pyplot as plt
import numpy as np
# Define the payoffs
Q = -3
R = -2
S = -4
T = -1
# Define the cooperation probabilities
p_A_C = np.linspace(0, 1, 1000)
# Calculate the expected utility for Alice
E_U_A_G = (R - S - T + Q) * p_A_C**2 + (S + T - 2 * Q) * p_A_C + Q
# Plot the expected utility
plt.figure(figsize=(10, 6))
plt.plot(p_A_C, E_U_A_G, label=r'$E[U_A(G)]$', color='blue')
plt.xlabel(r'Cooperation Probability $p^*(A_C)$')
plt.ylabel(r'Expected Utility $E[U_A(G)]$')
plt.title('Expected Utility of the Game for Alice')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(color='gray', linestyle='--', linewidth=0.5)
plt.ylim([np.min(E_U_A_G), np.max(E_U_A_G)])
plt.legend()
plt.show

Overall, the analysis and derived equations seem to correctly capture the dependence and provide a policy for determining the optimal cooperation probability in this correlated Prisoner’s Dilemma. From what I can tell based on the tests I’ve performed, the solution works as intended and aligns with my theoretical expectations from the payoffs.

Incorporating Correlation into Expected Utility

If you’re not convinced by the case where we assume that two rational agents make exactly the same decision given identical payoffs or by the extended case where the two rational agents converge on the same optimal mixed strategy policy, I present a third generalization which introduces noise into our model.

To model the dependence structure between the agents’ decisions alongside some natural uncertainty, let’s introduce a correlation parameter $ρ$ that captures the degree of correlation between Alice’s and Bob’s choices due to the common upstream factors, $V$ . We can think of $ρ$ as a measure of how likely it is that if Alice cooperates, Bob will also cooperate, and similarly for defection. This parameter will range from −1 to 1, where:

$ρ = 1$ indicates perfect positive correlation (Alice and Bob always make the same choice). When $ρ = 1$ , this model degenerates to our clone case.
$ρ = 0$ indicates no correlation (Alice and Bob’s choices are independent).
$ρ = - 1$ indicates perfect negative correlation (Alice and Bob always make opposite choices).

With this in mind, let’s redefine the probabilities ${^p}_{A} (B_{C} | A_{C})$ , ${^p}_{A} (B_{D} | A_{C})$ , ${^p}_{A} (B_{C} | A_{D})$ , and ${^p}_{A} (B_{D} | A_{D})$ to incorporate $ρ$ .

We assume the following relationships for the conditional probabilities based on $ρ$ :

${^p}_{A} (B_{C} | A_{C}) = \frac{1 + ρ}{2}$
${^p}_{A} (B_{D} | A_{C}) = \frac{1 - ρ}{2}$
${^p}_{A} (B_{C} | A_{D}) = \frac{1 - ρ}{2}$
${^p}_{A} (B_{D} | A_{D}) = \frac{1 + ρ}{2}$

These expressions ensure that the probabilities are consistent with the correlation parameter.

We can now substitute these probabilities into our expected utility equation for Alice from earlier:

$\begin{matrix} E [U_{A} (G)] & = (E [U_{A} (G | A_{C}, B_{C})] \frac{1 + ρ}{2} + E [U_{A} (G | A_{C}, B_{D})] \frac{1 - ρ}{2}) p^{*} (A_{C}) + (E [U_{A} (G | A_{D}, B_{C})] \frac{1 - ρ}{2} + E [U_{A} (G | A_{D}, B_{D})] \frac{1 + ρ}{2}) p^{*} (A_{D}) \end{matrix}$

Now, substitute the payoffs $R, S, T, Q$ and use $p^{*} (A_{C}) + p^{*} (A_{D}) = 1$ :

$\begin{matrix} E [U_{A} (G)] & = (R \frac{1 + ρ}{2} + S \frac{1 - ρ}{2}) p^{*} (A_{C}) + (T \frac{1 - ρ}{2} + Q \frac{1 + ρ}{2}) (1 - p^{*} (A_{C})) \end{matrix}$

Simplify further:

$\begin{matrix} E [U_{A} (G)] = (\frac{R (1 + ρ) + S (1 - ρ)}{2}) p^{*} (A_{C}) + (\frac{T (1 - ρ) + Q (1 + ρ)}{2}) (1 - p^{*} (A_{C})) \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = (\frac{R + S + ρ (R - S)}{2}) p^{*} (A_{C}) + (\frac{T + Q + ρ (Q - T)}{2}) (1 - p^{*} (A_{C})) \end{matrix}$

Combine terms:

$E [U_{A} (G)] = (\frac{R + S + ρ (R - S)}{2}) p^{*} (A_{C}) + (\frac{T + Q + ρ (Q - T)}{2}) - (\frac{T + Q + ρ (Q - T)}{2}) p^{*} (A_{C})$

$E [U_{A} (G)] = p^{*} (A_{C}) (\frac{R + S + ρ (R - S) - T - Q - ρ (Q - T)}{2}) + (\frac{T + Q + ρ (Q - T)}{2})$

Simplify the coefficient of $p^{*} (A_{C})$ :

$E [U_{A} (G)] = p^{*} (A_{C}) (\frac{R + S - T - Q + ρ (R - S - Q + T)}{2}) + (\frac{T + Q + ρ (Q - T)}{2})$

Because we’re looking to maximize $E [U_{A} (G)]$ , the optimal strategy for Alice depends on the sign of the coefficient of $p^{*} (A_{C})$ :

If $\frac{R + S - T - Q + ρ (R - S - Q + T)}{2} > 0$ , then $p^{*} (A_{C}) = 1$ . This implies that, if $ρ > \frac{Q - R - S + T}{- Q + R - S + T}$ , then $p^{*} (A_{C}) = 1$ .

Similarly, if $\frac{R + S - T - Q + ρ (R - S - Q + T)}{2} < 0$ , then $p^{*} (A_{C}) = 0$ . This implies that, if $ρ < \frac{Q - R - S + T}{- Q + R - S + T}$ , then $p^{*} (A_{C}) = 0$ .

In this section, we’ve incorporated the correlation parameter $ρ$ into our analysis to allow us to capture the dependency between Alice’s and Bob’s choices caused by common upstream factors. We’ve found that this extension suggests that the degree of correlation between the actions of the two players significantly influences their optimal strategies.

$p^{*} (A_{C}) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} 1 & if ρ > \frac{Q - R - S + T}{- Q + R - S + T} 0 & if ρ < \frac{Q - R - S + T}{- Q + R - S + T} \end{matrix}$

Specifically, when $ρ$ is sufficiently positive, there is a correlation threshold above which mutual cooperation becomes the dominant strategy for both players.

The Prisoners Do-Calculus

In the final most general case, we formalize the problem in the language of Pearl’s do-calculus. Instead of assuming a $ρ$ -model for correlation, we maintain a non-parametric perspective in this final stage.

We start again by defining the expected utility of the game to Alice:

$E [U_{A} (G)] = E [U_{A} (G ∣ do (A_{C}))] p^{*} (A_{C}) + E [U_{A} (G ∣ do (A_{D}))] p^{*} (A_{D})$

This time the expected utility of the game to Alice is the sum of the expected utility of the game to her given that she chooses to cooperate and the expected utility of the game to Alice given that she chooses to defect, weighted by the optimal probability that she does either. We now decompose the new terms $E [U_{A} (G ∣ do (A_{C}))]$ and $E [U_{A} (G ∣ do (A_{D}))]$ .

$E [U_{A} (G ∣ do (A_{C}))] = E [U_{A} ((G ∣ B_{C}) ∣ do (A_{C}))] {^p}_{A} (B_{C} ∣ do (A_{C})) + E [U_{A} ((G ∣ B_{D}) ∣ do (A_{C})] {^p}_{A} (B_{D} ∣ do (A_{C}))$

$E [U_{A} (G ∣ do (A_{D}))] = E [U_{A} ((G ∣ B_{C}) ∣ do (A_{D}))] {^p}_{A} (B_{C} ∣ do (A_{D})) + E [U_{A} ((G ∣ B_{D}) ∣ do (A_{D})] {^p}_{A} (B_{D} ∣ do (A_{D}))$

That is,

$E [U_{A} (G ∣ do (A_{C}))] = R \cdot {^p}_{A} (B_{C} ∣ do (A_{C})) + S \cdot {^p}_{A} (B_{D} ∣ do (A_{C}))$

$E [U_{A} (G ∣ do (A_{D}))] = T \cdot {^p}_{A} (B_{C} ∣ do (A_{D})) + Q \cdot {^p}_{A} (B_{D} ∣ do (A_{D}))$

And,

$\begin{matrix} E [U_{A} (G)] = R \cdot {^p}_{A} (B_{C} ∣ do (A_{C})) p^{*} (A_{C}) + S \cdot {^p}_{A} (B_{D} ∣ do (A_{C})) p^{*} (A_{C}) + T \cdot {^p}_{A} (B_{C} ∣ do (A_{D})) p^{*} (A_{D}) + Q \cdot {^p}_{A} (B_{D} ∣ do (A_{D})) p^{*} (A_{D}) \end{matrix}$

Given the dependence DAG earlier, we can incorporate our upstream variable $V$ into our refined expected utility calculation using do-calculus.

${^p}_{A} (B_{C} ∣ do (A_{C})) = \sum_{v} P (B_{C} ∣ A_{C}, v) P (v)$

${^p}_{A} (B_{D} ∣ do (A_{C})) = 1 - \sum_{v} P (B_{C} ∣ A_{C}, v) P (v)$

${^p}_{A} (B_{C} ∣ do (A_{D})) = \sum_{v} P (B_{C} ∣ A_{D}, v) P (v)$

${^p}_{A} (B_{D} ∣ do (A_{D})) = 1 - \sum_{v} P (B_{C} ∣ A_{D}, v) P (v)$

Substituting these probabilities back into Alice’s expected utility formula, we get:

Simplifying the expression:

$E [U_{A} (G)] = (R \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) + S (1 - \sum_{v} P (B_{C} ∣ A_{C}, v) P (v))) p^{*} (A_{C}) + (T \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + Q (1 - \sum_{v} P (B_{C} ∣ A_{D}, v) P (v))) p^{*} (A_{D})$ $E [U_{A} (G)] = (R \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) + S - S \sum_{v} P (B_{C} ∣ A_{C}, v) P (v)) p^{*} (A_{C}) + (T \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + Q - Q \sum_{v} P (B_{C} ∣ A_{D}, v) P (v)) p^{*} (A_{D})$ $E [U_{A} (G)] = ((R - S) \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) + S) p^{*} (A_{C}) + ((T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + Q) (1 - p^{*} (A_{C}))$ $E [U_{A} (G)] = (R - S) \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) p^{*} (A_{C}) + S p^{*} (A_{C}) + (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) - (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) p^{*} (A_{C}) + Q - Q p^{*} (A_{C})$ $E [U_{A} (G)] = ((R - S) \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) - (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + S - Q) p^{*} (A_{C}) + (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + Q$

This expression now shows the expected utility of the game to Alice in terms of her probability of cooperating $p^{*} (A_{C})$ and incorporates the dependencies through the common factor $V$ . We find that the expected utility of the game $E [U_{A} (G)]$ is maximized when:

$(R - S) \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) - (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + S - Q > 0$

$(R - S) \sum_{v} P (B_{C} ∣ A_{C}, v) P (v) + S > (T - Q) \sum_{v} P (B_{C} ∣ A_{D}, v) P (v) + Q$

If the inequality above is satisfied, then Alice should cooperate; otherwise, she should defect.

Confirmation

To test this most general form, we map it down to each of the particular cases we explored in the preceding sections.

Traditional Independent Case

In the first solution we assume independence between Alice’s and Bob’s choices. This means $P (B_{C} ∣ A_{C}, v) = P (B_{C})$ and $P (B_{C} ∣ A_{D}, v) = P (B_{C})$ .

We substitute these probabilities into our general utility function, yielding:

$\begin{matrix} E [U_{A} (G)] = R \cdot p^{*} (B_{C}) p^{*} (A_{C}) + S \cdot p^{*} (B_{D}) p^{*} (A_{C}) + T \cdot p^{*} (B_{C}) p^{*} (A_{D}) + Q \cdot p^{*} (B_{D}) p^{*} (A_{D}) \end{matrix}$

This simplifies down to:

$E [U_{A} (G)] = p^{*} (A_{C}) [(R - S - T + Q) P (B_{C}) + S - Q] + (T - Q) P (B_{C}) + Q$

This is exactly the expression we found for Alice’s expected utility in that section, so pat on the back, onto the next section.

Clone Case for Cooperation

In the second model, Alice and Bob are assumed to make exactly the same decision, implying perfect correlation. Thus, $P (B_{C} ∣ A_{C}, v) = 1$ and $P (B_{C} ∣ A_{D}, v) = 0$ . This simplifies the general solution as follows:

$\begin{matrix} E [U_{A} (G)] = R \cdot 1 p^{*} (A_{C}) + S \cdot 1 p^{*} (A_{C}) + T \cdot 0 p^{*} (A_{D}) + Q \cdot 0 p^{*} (A_{D}) \end{matrix}$

$\begin{matrix} E [U_{A} (G)] = p^{*} (A_{C}) (R + S) \end{matrix}$

Because $R > S$ , $E [U_{A} (G)]$ is maximized when $p^{*} (A_{C}) = 1$ . Just as we anticipated, Alice should always cooperate, aligning with our expectations again.

Identical Mixed Strategies

In the next model, we extend and suggest that Alice and Bob converge on the same mixed strategy. That is, ${^p}_{A} (B_{C} ∣ A_{C}, v) = p^{*} (A_{C})$ and ${^p}_{A} (B_{C} ∣ A_{D}, v) = p^{*} (A_{D})$ . This gives us:

$\begin{matrix} E [U_{A} (G)] = R \cdot p^{*} (A_{C}) p^{*} (A_{C}) + S \cdot p^{*} (A_{D}) p^{*} (A_{C}) + T \cdot p^{*} (A_{C}) p^{*} (A_{D}) + Q \cdot p^{*} (A_{D}) p^{*} (A_{D}) \end{matrix}$

This is the same result we expected as well, confirming our general causal model.

Correlated Mixed Policy

In the final model, we introduced correlation parameter $ρ$ to incorporate possible noise.

We make the following definitions:

${^p}_{A} (B_{C} ∣ A_{C}, v) = \frac{1 + ρ}{2}$

${^p}_{A} (B_{D} ∣ A_{C}, v) = \frac{1 - ρ}{2}$

${^p}_{A} (B_{C} ∣ A_{D}, v) = \frac{1 - ρ}{2}$

${^p}_{A} (B_{D} ∣ A_{D}, v) = \frac{1 + ρ}{2}$

From this, the corresponding $ρ$ -model falls out.

$\begin{matrix} E [U_{A} (G)] & = R (\frac{1 + ρ}{2}) p^{*} (A_{C}) + S (\frac{1 - ρ}{2}) p^{*} (A_{C}) + T (\frac{1 - ρ}{2}) (1 - p^{*} (A_{C})) + Q (\frac{1 + ρ}{2}) (1 - p^{*} (A_{C})) \end{matrix}$

The language of do-calculus is quite appealing for its generality, and it, in my eyes, models the reality of the problem at hand extremely well.

Conclusion

This framework implies that, despite typical Game Theory 101 lectures suggesting 100% selfish play in one-shot games like this, if you believe that you think sufficiently similarly to your counterparty, the game theory optimal policy would be to faithfully cooperate and both walk away free.

A broader conclusion of this analysis is to always consider higher-level dependencies, even when two things seem to be perfectly independent. We should also include all possible information into our decisions, and this includes the decisions themselves. In this Prisoner’s Dilemma situation, we can consider this in some sense to be the opposite of “adverse selection”. Oftentimes, in adversarial games, conditional on performing an action, you’re less happy. There are many possible reasons for this, but a common reason is that you’re acting in a market and your ability to perform an action means that no one else in the market was willing to do what you just did, which gives you information that you might be making a mistake. This could be hiring a candidate where your ability to hire them means no other firm wanted them at the price you’re willing to pay. Or this could be winning an auction where your winning means that no one else was willing to pay the price that you paid. However, in the case we have at hand, there’s a sort of “advantageous selection”. This is because, if you choose to cooperate, now you get extra information that someone else in a similar position also likely cooperated as well, which is quite a pleasant type of selection.

For those who remain compelled by the original argument that, “still, if you know your opponent is going to cooperate, you’re better off defecting to serve no time instead of 1 year”, I might share some of my ideas on why I suspect that the recursive expected utility maximization decision algorithm that I present is superior in a follow-up essay. But for now, I’ll just say that while the Causal Decision Theorists are stuck in their (defect, defect) “rational” Nash equilibria, my co-conspirators and I will be faithfully cooperating and walking free into the warm sun of Pareto Optimality.

Acknowledgements: Thank you Alok Singh, Baran Cimen, Keegan McNamara, and Paul Schmidt-Engelbertz for reading through the draft and providing helpful guidance.

A Case for Cooperation: Dependence in the Prisoner’s Dilemma

TL;DR

The Traditional Analysis

Probabilistic Play

The Clone Case for Cooperation

Everything is Correlated

Causal Modeling 101

Independent Case (Optional)

Incorporating Dependence into Expected Utility

Optimizing (Optional)

Interpretation

Incorporating Correlation into Expected Utility

The Prisoners Do-Calculus

Confirmation

Conclusion