The computational complexity of progress

Cross-posted from Telescopic Turnip.

Artem Kaznatcheev has a curious model about the evolution of living things. When a population of creatures adapts to their environment, they are solving a complicated mathematical problem: they are searching for the one genome that replicates itself the most efficiently, among a pantagruelian pile of possible sequences. The cycles of mutation and natural selection can be seen as an algorithm to solve this problem. So, we can ask, are some evolutionary problems harder than others? According to Kaznatcheev, yes – some features are easy to evolve, some others are outright impossible, such that they can never be reached on planetary timescales. To tell the difference, he defines what he calls the computational complexity of a fitness landscape.

Computational complexity is a term from computer science. It describes how many steps you need to solve a given problem, depending on the size of the problem. For example, how long does it take to sort a list of n items, as a function of n? (If you do it right, the number of operations for sorting is proportional to n×log(n), written O(n log n). Unless you happen to be sorting spaghetti, then you can do it in n operations.) What is the equivalent of this for biological evolution?

Mountains and labyrinths

To get an intuition, consider a bug that can only mutate on two dimensions: the size of its body and the length of its legs. Each combination of the two has a given fitness (let’s define it as the number of copies of its genome that gets passed on to the next generation). So we can draw a 2D fitness landscape, with red being bad and cyan being better:

In the middle, there is a sweet spot of body mass and leg length that works great. Say our bug starts in the bottom left; after each generation it will generate a bunch of mutant offspring which spread around the current position. Due to natural selection, the mutants closest to the center will reproduce more, and if you repeat the process, the bug population will gradually climb the gradient towards the top of the fitness mountain.

Evolution in O(eⁿ)

The mountain range metaphor is actually pretty bad. Kaznatcheev offers a better one: a fitness landscape is a maze. Let’s look at two other examples:

Like the first one, these have no local maxima, there is only one global fitness maximum and, as long as you climb the gradient, you should eventually reach it. What distinguishes the two landscapes is how they behave as we add dimensions. Instead of just looking at body size and leg length, we also allow our bug to change colour, grow horns, use the the sky’s polarized light as a compass, or pretty much any weird survival strategy a bug could possibly come up with (and we all know bugs can get very creative when they evolve). As we consider more dimensions, the two landscapes above become dramatically different.

The important thing here is called epistasis: if you have two different mutations at the same time, do you get the same effect as if you had them separately? For example, having an optical nerve alone doesn’t do much, and neither does an isolated eyeball. But if you have both, you can see stuff. So there is strong epistasis between eyeballs and optical nerves.

For the landscape on the left, the two dimensions are independent (there’s no epistasis). Any progress you make in body size is simply added to the progress you make with leg length. For the perfectly linear gradient on the left, a new mutant can either fall in the better half of the space, or in the worse one, so there’s a ¹⁄₂ chance there is at least some progress. This doesn’t change as you add dimensions – there’s still one good and one bad direction and they are equally likely. So the probability of finding better mutants doesn’t depend on genome size – the computational complexity of this evolution problem is O(1).

Now look at the landscape on the right. Here, there is epistasis everywhere, forming a narrow path meandering through the plane. When the bug reproduces, there is only a small set of mutations that will lead to progress. Another set of mutations go backwards, and all other mutations take it out of the path, leading to ineluctable doom. Add more dimensions, and you get a tangela of a fitness landscape twisting and twining from one dimension to another and back. The fraction of mutations that are still on the path becomes vanishingly small as the genome size increases, and it does so at an exponential rate^[1]. In other words, the complexity is O(eⁿ). Even if there are no local fitness maxima, it’s basically impossible to reach the fitness optimum, not even in billions of years. Remember the optical nerve and eyeball problem: for a while people thought it was too complicated for natural selection alone and that there was probably some divine intervention somewhere. Now, we have a clear idea of how the eye evolved, but it’s indeed a very meandering path, and it only led us to a weird fitness optimum where the retina is inside-out.

With evolution, we don’t get to chose the algorithm. Its heart is always the good old random selection + natural selection procedure. What I like to do, however, is apply what we learn from evolution to human progress. In that case, we may even have a chance to pick the best algorithm to navigate the labyrinth.

The maze to Utopia

Like epistasis in biological evolution, there is epistasis in social and technological progress. There’s no benefit to landfills if there is no garbage collection, and no benefit to garbage collection without somewhere to put the trash. That’s all assuming people own trash cans and are willing to use them. So the problem of trash disposal is at least a little bit labyrinthic.

A lot of biotech people I know seem to have the 19th-century vision of a genius working out all the equations, creating an invention and making a fortune. Real-life technological progress is less predictable: major changes take multiple steps of back-and-forth interaction between inventors and the rest of the world. New inventions change the economy, then the change in the economy opens the door for new inventions.

One example that comes to my mind would be the development of AI, and so-called AI winters. It’s not that people didn’t try their best to come up with solutions to stagnating progress; they did, but those attempts didn’t lead anywhere. And then, when everybody was about to give up, this happened instead: cheap CPUs → video games → market for good graphics → cheap graphics cards → parallel computing → GPU-based deep learning → AI writing rap lyrics^[2]. I just gained access to DALL·E-2, so I’m delighted to offer you this picture of a turnip walking through a labyrinth:

To make this possible, we had to take all the right turns in the progress maze to get to the circumstances that made deep learning possible. We were never certain to get there at all. It’s easy to imagine a timeline where the first video games were not as fun as Tetris, people quickly got bored, gaming never took off and neural networks never happened. If the progress landscape is tortuous enough, some possibilities will simply never be reached. (Another example: Hegel → Marx → Stalin → Nuclear threat → ARPANET → Internet → smartphones → better lithium-ion batteries → electric scooters^[3].)

On the other hand, think about lasers. The development of the laser is an incredible story that took a lot of work and a long series of genius ideas. You had to get to the black-body radiation problem, then come up with quantum mechanics, stimulated emission, the ammonia maser, then make the first laser prototypes, and turn that into something that can be mass-produced, so you can finally sell $5 laser pointers with a swirl-shaped beam. It was definitely hard. But it was straightforward – every step followed logically from the previous one. As far as I can tell, the process that led us to the laser didn’t depend on any other economic advance. Any intelligent animal interested in developing lasers would probably manage to do so, even if it takes considerable effort.

This makes me wonder about all the simple, cheap, incredibly effective gadgets we would be perfectly able to invent, but that we will never see because the path that leads to them simply doesn’t happen. Maybe there actually is one weird trick to lose weight that makes doctors hate you, but it requires the right combination of garbage collection system, birthday rituals and onion trading legislation. Maybe in the timeline without neural networks, Project Plowshare was a major success instead, and who knows what the hell teenagers are up to in that world. (Our version of Tiktok has better beauty filters, though.)

Models and metis

In Samzdat’s classic the Uruk Machine, two radically different progress algorithms are compared: the traditional metis and its replacement, the modern episteme. Metis, as defined by James Scott in Seeing Like a State, is based on cultural evolution. People perpetuate traditions and try new things out, without any clear idea of the causes and consequences of what they are doing. Eventually, the successful practices are adopted by everyone. The result is a complicated culture of undecipherable traditions that fit the local context perfectly. Nobody has a single clue on how they work, so of course attempts to improve them rationally usually fail. Episteme in the exact opposite: people have a clear model of the world, and they optimize the world based on this model.

The development of lasers was a low-epistasis progress landscape, and it turned out the epistemic approach worked great. On the other hand, neural nets were a high-epistasis labyrinth, and the development of AI looks more like shamanism than rational engineering. Maybe this is not a coincidence. When the landscape is smooth, you can test little things independently, then combine all of it to design a complicated system, and it will actually work. On rugged progress landscapes, however, episteme will probably fail. Your calculations may be correct, but when everything has strong epistasis with everything, there is always something you couldn’t plan and you end up falling off the path, to the ravine.

Maybe that was the problem with GMOs like the golden rice: it sounds like a perfectly fine way to prevent people from going blind, but then you’re entering the realm of food, which has a long tradition of pure metis, so people might just decide they don’t want to eat rice with an unnatural colour. The path to solve the second part is going to be much more unpredictable.

If you read Eric Hoel’s review of The Dawn of Everything, who won this year’s ACX review contest, you may remember the Sapiens Paradox, or why it took 50,000-200,000 years for anatomically modern humans to adopt formal social organizations. My favourite solution is that it took a lot of time because finding an organization that works does in fact take a lot of time.

Think of the traditional culture of your home town. How many equally weird cultures would be possible in principle? Somehow, Zoroastrians managed to prevent crime by all agreeing that criminals spend the afterlife in a place with stinky wind instead of a nice-smelling one. That’s indeed a possible solution to the crime problem. But for one culture that works, how many are doomed to fail? There’s the culture where all adolescent males must dive in a volcano to determine who’s the gang leader, the one where hemlock looks delicious (you can’t prove it’s not), the one where you have to commit suicide before 10 to go to unlimited heaven, and so on. The space of possible cultures is so huge, and the fraction that are actually stable is so small, that 50,000 years don’t sound like too much. After all, 50,000 years is only 2500 generations of 20 year-olds. If the total number of tribes is small and people die young (so they can’t witness long-term processes), it’s actually amazing that they could figure out stuff like religion in so few attempts. Ants are spectacularly good at this kind of thing, but they’ve had more than 100,000,000 years to refine their management practices (with a much shorter generation time!).

But wait, there might be a way to make things faster. As always, other living organisms came up with it long before us.

Blurry walls

Let’s come back to pure evolutionary biology. The living world is full of oscillators, like the circadian rhythm, root circumnutation, or your heartbeat. Here’s a recent paper from Lin et al who wanted to figure out how these oscillators could possible evolve. So they they ran simulations of genetic networks, when the individuals are more likely to reproduce when some gene turns on and off at regular interval. After a while, their virtual organisms eventually started oscillating. But it took really long.

Here is a fitness landscape from the paper, showing how well an organism oscillates as a function of two parameters of the genetic circuit:

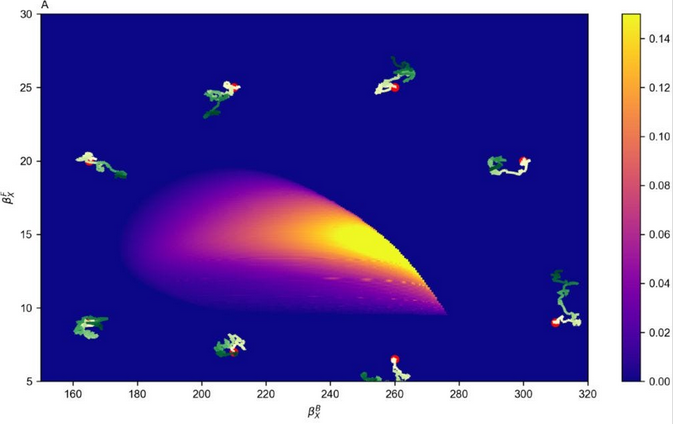
The zigzagging things are evolving populations starting from various positions in the landscape. The problem here is that they all start in regions where there is simply no oscillations at all. So there’s no gradient to climb. All they can do is diffuse randomly through the landscape, until they meet the region where natural selection can occur. This is like falling off the path of the labyrinth in the previous paragraphs: once you’re off the track, you can’t know where to go until you find it again by chance.

So Lin and colleagues added random fluctuations to the circuits. I would expect random noise to make it harder to construct a working oscillator, as it would make it less reliable, but the opposite happens:

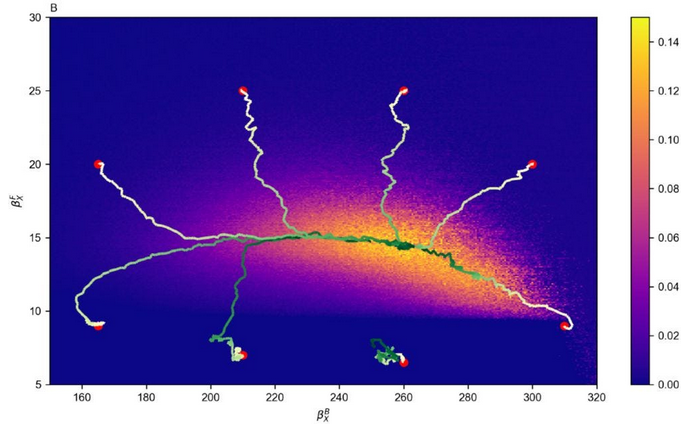
What’s going on? When there’s no fluctuations, all the organisms in the population stand at the exact same point in the fitness landscape. But randomness causes different cells in the population to spread out around the average phenotype like a little cloud. This allows them to test not only the average phenotype, but also the ones directly around it. If it turns out one of these neighbouring phenotypes is much better, this will give a statistical advantage to the population, so it will reproduce further. And then, it has more opportunities to find the actual mutations that would produce the better phenotype. In the simulations, adding randomness blurred out the fitness landscape, making it quicker to navigate.

Applying this to progress, we come back to metis: instead of having one grand unified plan for Utopia, we have many tiny local modes of organizations, each trying out little changes in random directions. Sometimes, one will hit a successful change and the rest will copy it. On the local level, many of these changes will be detrimental, but overall, it makes it easier to find intricate, unpredictable ways to succeed. In other words, episteme might be more immediately effective, but metis is more evolvable. This might be a reason why markets can sometimes lead to surprisingly good outcomes: markets are mostly based on episteme, but they still allow for a lot of noise. Some people will try random things that do not exactly follow what they were told in the business school. If they are successful, other companies will copy their strategy. If they are really successful, their strategy will end up being taught in business schools. Bad organizations will just wane out while the successful ones will be imitated by everyone else.

The exact opposite, of course, is having a central authority calculating the optimal policy with linear programming and enforcing it equally everywhere. This might be incredibly effective for low-epistasis tasks like sending satellites to space, but it will fail brutality as soon as the landscape becomes rugged. Any failure in this central plan means failure of the whole system. If you read Mencius Moldbug, you’ll find him repeating that capitalist companies are all little absolute monarchies, with a CEO as royalty, so if we want our State to be as effective as Amazon, we should go back to a monarchy. I think he’s getting everything backwards: Amazon works not because the company system is intrinsically good, but because there were hundreds of others would-be Amazons who all tried slightly different things. One of them was successful, but many other collapsed – which is not something I’d want to happen to a state.

In a way, this is both an argument for and against markets: if the success of markets comes from a better evolvability, then it might be possible to extract just this feature and add it to your favourite non-market utopia, to get the advantages of markets without the inconvenience. Could you design a system of evolvable kolkhozes? I’ll leave that as an assignment to Marxist readers.

Or maybe the point is that such systems cannot be designed, as they’re hidden in the most inaccessible corners of the labyrinth. The space of possible cultures is full of utopias with eternal peace and universal love, but they are just too insane for humans to ever come up with them.

Summary

In evolution, some fitness landscapes may have lower or higher computational complexity, depending on how “labyrinthic” they are,
Higher computational complexity is due to traits interacting with each other,
Similarly, the road to some social and technological innovations may be straightforward, or require the right unpredictable circumstances to emerge first,
Episteme is better at low-complexity problems, but metis (or cultural evolution) can navigate more complicated parts of the labyrinth,
Some biological systems can evolve faster by becoming less robust, as noise allows to explore the surroundings of the current state. Implications for Utopia design are discussed.

Thanks to Justis Mills for feedback on the draft.

^
If you’re bad with dimensions, imagine a lattice. In 1D, you have 2 neighbours. In 2D, you have 8, in 3D you have 26 and so on. If only one neighbour leads to progress, then the number of possible bad moves grows exponentially with the number of dimensions.
^
“Tell the gang I never break my promise mang”, said the superintelligent punchline-maximizer before turning the last atom of the solar system into a mic to drop.
^
This timeline is also the one where “nuclear bombs → internet → cute cat pictures” and “nuclear bombs → postwar Japanese culture → anime” collide to produce catbois.