Understanding Selection Theorems

This post is a distillation of a corpus of ideas on Selection Theorems by johnswentworth, mainly this post. It was made for EA UC Berkeley’s Distillation Contest.

Introduction

Selection Theorems are tools for answering the question, “What will be the likely features of agents we might encounter in an environment?” Roughly speaking, if an environment selects for agents according to some metric, then Selection Theorems try to give us some guarantees or heuristics about the classes of agents that will be highly fit in the environment.

This selective pressure need not be biological. If an AI researcher scraps some agent designs and keeps others, or a set of market traders can thrive or go bankrupt based on their trading performance, then these might also be situations where Selection Theorems can apply.

The value of strong Selection Theorems is quite alluring: if we can make specific claims about the types of agents that will arise in particular environments, it might become easier to know what aligned systems look like and how to make them. They may also be instrumental in resolving our general confusion about the nature of agency.

The goals of this post will be to provide intuition and examples for the notion of agent type signatures, define and describe Selection Theorems through an example, and discuss what future research might look like. I do not assume any technical background from readers, other than a baseline familiarity with ideas like agency and expected utility.

A Toy Scenario

Suppose I am trying to build a robotic agent which mops and polishes floors. I have two prototype mopping agents, A and B, with different internal architectures:

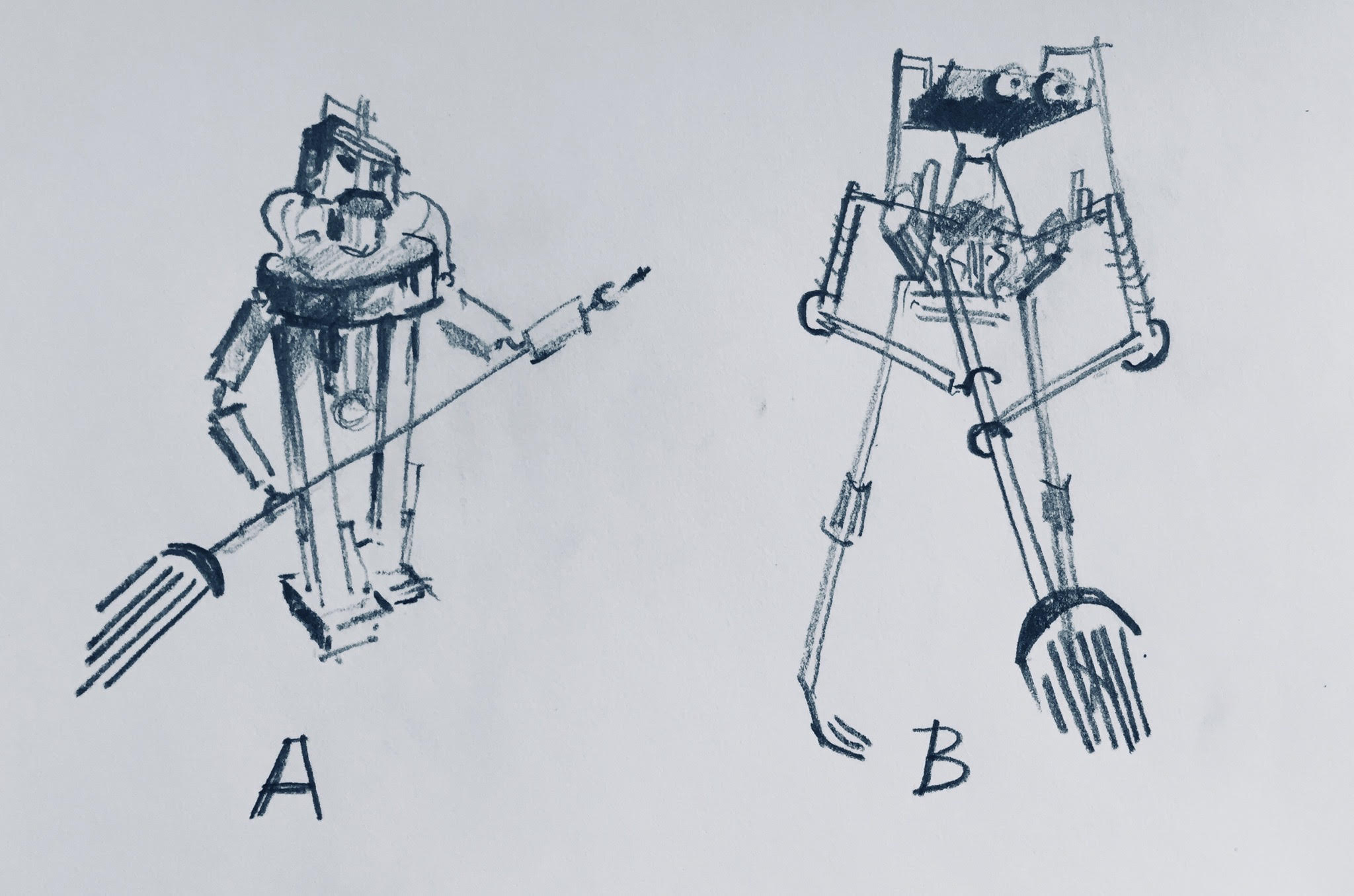
Both agents are relatively safe and competent at this job, but there are a few key differences:

Agent A normally thinks rooms are cleanest when the floors are mopped and polished, but after polish is applied, it thinks rooms are cleanest without polish. As a result, it quickly becomes stuck applying and removing polish. Agent B shows no such problem. It mops floors, polishes them, and then moves on to the next room.
Agent A cleans any mess it sees. However, if I hold a picture of a different room close to Agent A’s camera, it immediately behaves as though it is in the room of the picture, forgetting its previous surroundings. Agent B, meanwhile, is robust to these tricks: if it begins cleaning, and halfway through is shown a picture of a different room, it recognizes that its view is being obstructed and tries to move to get a better view of its real surroundings.

There is a sense in which Agent A is less effective and Agent B is more effective with respect to my desires. Even though A and B may have broadly similar views of what makes a clean room, Agent B seems better suited to complete the task in the real world. As I continue prototyping these agents, preferring only the most robust cleaning robots, the end result will be agents structurally less like A and more like B.

Agent Type Signatures

The above observations are a good segue to what John calls the type signature of an agent. In computer science, type signatures refer to the input and output data structures of functions. For example, a function with a type signature $R \to R$ takes real numbers as input and outputs a real number. The functions “add 1” and “multiply by 2″ both share this type signature, despite being different functions. Type signatures are interested in capturing the general structure of a function rather than its specific behavior.

Insofar as agents might just be special types of functions, thinking about their type signature makes sense. In particular, John sees an agent’s type signature as collectively referring to the subcomponents of agents, the data structures or mathematical objects that represent these components, the high-level interactions between subcomponents, as well as the embedded relation between components and what they are actually supposed to represent in the environment.

As an example for part of an agent’s type signature, many agents have “goal” components that rank world states (which are themselves components represented by their own data structures). One can then represent goals through the data structure of utility functions, or alternatively as committees of utility functions, or something entirely different.

Type signatures can make or break the effectiveness of an agent. Let us again consider the mopping agents, and in particular the data structures representing their key components:

The fact that Agent A became stuck adding and removing polish indicated that the data structure representing its goal failed to define a consistent preference ordering over world states. In terms of the type signature of A’s goal component, the fact that it took the current world state as input proved to be a problem. Agent B’s goals were more stable since they were not dependent on the current state of the room, reflecting a more robust underlying data structure with a consistent preference ordering.
Agent A’s world model corresponded poorly to its embedded environment. From Agent A’s behavior when shown a picture of a new room, we see that the data structure representing world states in A’s world model was something akin to simple pixel arrays—its momentary visual view of rooms. Although vision of things and things themselves are tightly related in most situations, Agent A was still vulnerable to tricks which prevented it from doing what I wanted. The value of Agent B’s more successful world model came from its ability to distinguish its perception from its model of the environment, and leverage perception-independent memories of its surroundings. Agent B internally represented its environment on a lower level, and was thus able to recognize and account for incomplete or unreliable perceptual inputs.

Another aspect of agent type signatures is the manner in which component outputs directly interact with the environment. Consider a third cleaning robot, Agent C, whose type signature has a decision-making component that outputs natural language directives (like “put the mop in the water bucket” and ” walk forward three steps”) rather than motor controls. Agent C would be wholly useless to me: it would just stand unmoving, with a mop lying beside it, repeating “pick up mop,” “pick up mop.”

We see from these considerations that a well-chosen type signature plays a large part in the success of an agent. Of course, the value of type signatures is completely environment-dependent. For example, although Agent A was ineffective because it represented world states as pixel arrays, an agent playing Pac-Man would do well with such a world state data structure, since a picture of a Pac-Man screen tells an agent everything they need to know to play well.

Selection Theorems and an Example

In any environment that exerts a selection pressure on agents, we might expect high-fit or optimal agents (with respect to the selection criteria) to exhibit particular sorts of behaviors or type signatures. Selection Theorems are any result that shows what these optima looks like for a particular class of environments. According to John:

A selection theorem typically assumes some parts of the type signature (often implicitly), and derives others.

John gives many examples of Selection Theorems. I will focus only on coherence theorems in this post; they strike me as the archetypal example.

Much has already been said on LessWrong about coherence theorems, and so I will not go into specifics or proofs. Instead, my goal here is to explicitly reframe them in the language of Selection Theorems. To do so, we are forced to ask, “What exactly do the coherence theorems assume about agent type signatures, and what do they derive?” Let us list these assumptions in brief for a slightly simplified formulation of a coherence theorem:

There is an environment where agents are selected for by their ability to maximize a resource. The resource can be anything (money, well-being, reproductive fitness, etc.), so long as it is fungible and we can unambiguously measure how much an agent has.
As part of their type signatures, all agents have a set of world states.
Actions for agents are represented as bets, where a bet might cost resources upfront but might pay out resources based on the resulting world state.
Finally, all agents have a decision-making component which chooses among sets of possible actions. Beyond this, we do not need to make any assumptions on exactly how the decision-making component works.

Once all of these assumptions are satisfied, it is mathematically guaranteed that the optimal decision-making mechanism for an agent this environment will be equivalent to an expected utility maximizer, with respect to the resource that is selected for! In other words, agents which do not have decision-making components of this form are strictly outcompeted by alternate agents which do—this is the mechanism of the selection.

Next Steps for Selection Theorems

What are some key takeaways from coherence theorems? For one thing, the stringency of the assumptions means that, in their current form, coherence theorems do not directly apply to agents in the real world. Many people make the mistake of invoking them without making sure assumptions apply. Of course, coherence theorems certainly have useful implications, insofar as the real world has high-level equivalents to resources, and insofar as many real-world actions can be modeled as bets. But as John elaborates in this comment, they are flawed. Among other things:

“Resources,” as they are defined in the theorem, do not seem to exist on a low level; they are not baked into our environment. For instance, in biology, reproductive fitness is a useful label we can apply to lifelike systems, but it doesn’t represent a direct physical quantity.
Even if there are useful abstractions in the real world that satisfyingly behave like “resources,” it is strange that the coherence theorems have to assume them a priori; we’d prefer to derive the notion of a resource within the Selection Theorem itself. In other words, the notion of resources should arise without assumption from the proof, in the same way that the notion of probability arises without prior assumption from current coherence theorems.
There are variants of the coherence theorem setup where maximizing expected utility is not the optimal, or at least not the only optimal, type signature that will be selected for. See John’s Why Subagents? post for details.
Agents in general might not even have the components or representations required by the theorem. This is a part of a broader open question: Does Agent-like Behavior Imply Agent-like Architecture?

These concerns are paralleled in many other existing Selection Theorems: their starting assumptions about the environment and agency often too narrow and hard to apply. What we ultimately want is a family of Selection Theorems which make as few assumptions as possible about the environment or agent type signature, while deducing as much as possible about the optimal type signature and behavior of agents. Further, in John’s words:

Better Selection Theorems directly tackle the core conceptual problems of alignment and agency

In these respects, coherence theorems (and our current scattering of existing Selection Theorems in general) are woefully incomplete.

Aside from merely improving existing theorems, new Selection Theorems might venture to explain and sharpen broad classes of fuzzy observations about existing agents, answering questions like “Why don’t plants develop central nervous systems (brains)? What assumptions about plants and their environments imply brains are being selected against, if at all?” John gives a detailed overview of what the Selection Theorems research program might investigate and what sorts of results it might eventually deduce. I suggest that the interested reader continue there.

Overall, I see Selection Theorems as a promising approach to chipping away at our confusion behind agency. Future research may involve an empirical component, but the conceptual nature of this research program suggests that new paradigms for understanding agency may be a couple good insights away.