[ASoT] Some thoughts about deceptive mesaoptimization

Editor’s note: I’m experimenting with having a lower quality threshold for just posting things even while I’m still confused and unconfident about my conclusions, but with this disclaimer at the top. Thanks to AI_WAIFU for discussions.

I think of mesaoptimization as being split into different types: aligned (which is fine), misaligned (which is bad), and deceptively aligned (which is really bad—I draw the line for deceptively aligned when it actually tries to hide from us instead of us just not noticing it by accident). I mostly think about deceptive mesaoptimization, and I think of regular misaligned optimization as basically an easier case because at least it’s not trying to hide from us (what it means for it to actually be “trying to hide” is kinda fraught anyways so this sidesteps that). In particular, I think of mesaoptimizers as being dangerous because they fail in a malign way (I don’t think mesaoptimization itself is necessarily bad, and preventing it doesn’t seem obviously good).

OOD-focused framework of deception

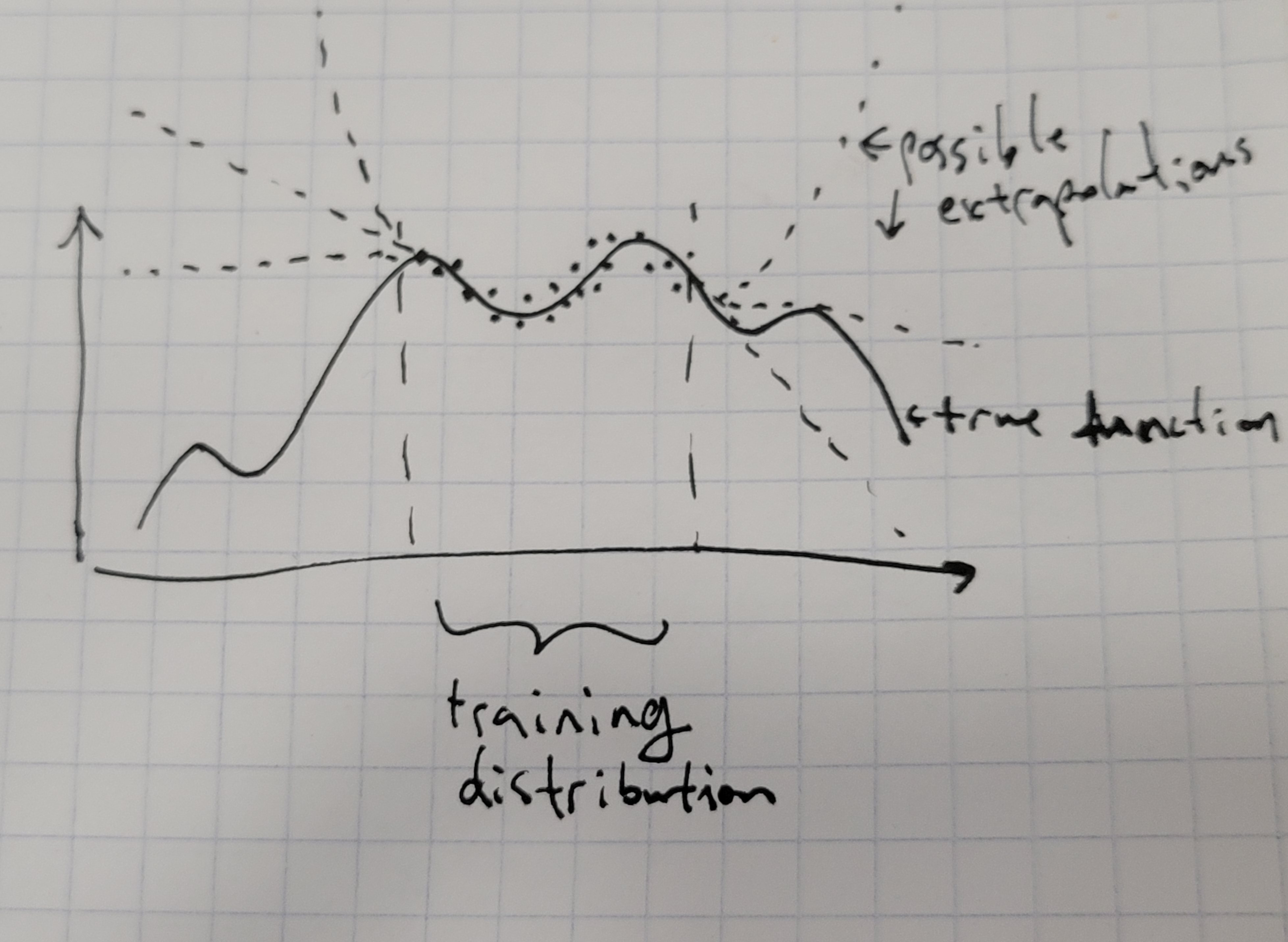
One framework for thinking about deceptive mesaoptimizers that I used to use a lot was that they would be good on the training distribution, but then do bad things out of distribution. In this framework, what we would do is then to try to somehow tell during training whether a model is going to do bad things out of distribution, and only keep the ones that don’t, or something along those lines. The intuition is that the mesaoptimizer cares about something in the real world, but it knows that if we catch it then it will not be able to achieve its goals in the real world, so it behaves normally on the training distribution when we’re looking at it but then in deployment it goes and does evil things to satisfy its mesaobjective. Importantly, pursuing the mesaobjective hurts the base objective (since we’re only focusing on inner alignment here we can assume that the base objective is accurate), so deployment is the only time where it can do evil things without getting itself removed.

The main reason here that deception happens is that your base objective isn’t being integrated over the set of all possible states. In theory, if we could enumerate the entire (huge) input space, we could eliminate deceptive behavior entirely. We’d just simply test every single input and see how whether there are any regions where the model does a treacherous turn and consequently tanks the base objective (for now I’m trying to isolate inner alignment so I’m assuming we’ve solved outer alignment and have a value function that we can just query). If there is nowhere in the entire input source where the model does a treacherous turn, then congratulations, your model is, for all intents and purposes, indistinguishable from being not deceptively aligned. (Non-deceptive inner misalignment is very similar except the mesaoptimizer won’t be trying to hide from you.)

In practice, the input space is absolutely enormous, and it’s completely and utterly infeasible to enumerate it. Still, we might think to approximate that “perfect” red teaming by doing a really good approximation with loads of input instances sampled from a broad distribution, possibly with the help of other NNs. Unfortunately, I think this approach is fundamentally doomed, no matter how good the red ranking distribution is made. For this to work, the entire distribution of possible inputs in the real world would have to be covered by the red teaming distribution, and any small imperfections are potential points of leverage for the mesaoptimizer. Aside from some contrived existence proofs like the RSA2048 example (which are admittedly very useful for thinking about these things so I use them a lot despite the contrivedness), there are simply many things that could pop up in the real world (and especially the future) that we simply cannot predict/simulate, and that would be a giveaway signal of being in the real world.

Given an imperfect red teaming distribution, penalties for discovered deceptive behavior incentivizes the mesaoptimizer to shift probability mass from those regions into regions of the input space that are not covered by the red teaming; essentially, the model could learn just as well learn to not be caught deceptively mesaoptimizing, rather than not to mesaoptimize. Two possible ways this could swing towards the former are if either a) the mesaoptimizer is able to convergently gradient hack to ensure that between the two equal-training-loss options the training process goes into the one that preserves the mesaoptimizer, or b) mesaobjectives that imply deceptive behavior are easier to learn than those that imply honest behaviors (this one is especially likely to happen if the base objective is weird and complicated, as human values probably are, since all the simpler, easy to learn approximations are misaligned). I think both of these have a pretty good chance of being true, and would result, in effect, in models learning to hide from oversight.

So, we can’t possibly cover the entire space of possible inputs that could be encountered in deployment, and if the mesaoptimizer retreats into one of the states we didn’t think of then we’re done for, and it has a pretty big incentive to do so. This means that black box approaches, where we try various inputs while assuming no knowledge about the model itself, are kind of hopeless.

So actually although we care about the model’s behavior in situations we might encounter in the future, we can’t specify that yet in our training loss. So, if we optimize for this loss function, if it turns out that deception is favored by the prior defined by our learning process (which seems plausible), then even if we reach an optimum of this training loss our thing still might be deceptive outside of the training distribution. The other way things could go wrong is if our optimizer is not good enough. Then, we might just settle with a suboptimal deceptive model because our optimizer is unable to find the global min. This connects to the frame of inner alignment as a problem of imperfect optimization. In practice we get a combination of both of these problems at once: we can’t find the optimum of the training loss defined by our training distribution, which would allow for deception, and even if we could it might still be deceptive.

Unforeseen consequences framework of deception

(Update: I no longer think of the failure introduced in this section as purely an inner alignment failure, but rather as a more general problem with training consequentialist systems.)

However, I think there’s a completely different frame from the whole out of distribution / “it only becomes evil in deployment” frame that I’ve been thinking a lot about. So one thing we might think is that maybe we can just do whatever oversight we did during training but during deployment as well, and it might have some competitiveness problems, but it seems like it would at least be a good starting point. Unfortunately, I think there are some subtle problems with this that totally break it and analyzing those problems brings us to the other framing of deception. I think these problems show up in the previous frame too.

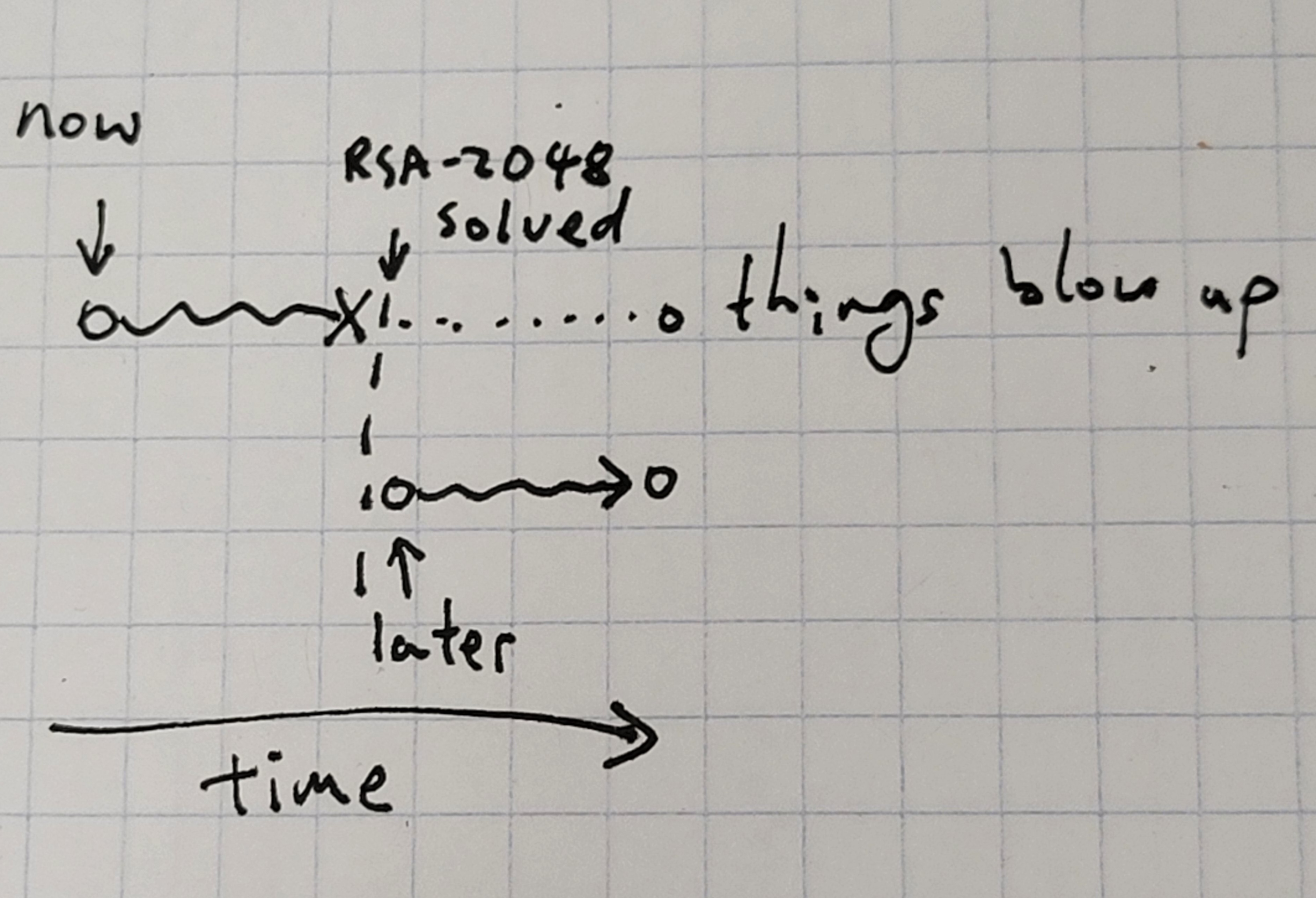
So let’s say the model proposes some action, and we want to know whether the action would be safe to implement. Then, assuming we have some world model, we can simulate the model’s action out, and see whether something bad happens (I’m assuming for now that we know something is bad when we see it, because we’re focusing on inner alignment. This is definitely not trivial or remotely solved and is a big part of outer alignment.) This is also roughly what we’d do for the training procedure in the previous frame. The problem is that this world model is completely impossible. Aside from the fact that it’s smaller than the world and therefore can’t fit the world, it’s also susceptible to RSA2048-like problems, where there are certain states of the world where we know we can be in, but can’t actually produce without enormous cost. Another example would be simulating a future where more powerful computers exist; we can’t do that on current computers obviously. And of course, RSA2048 is again just a particularly sharp example of the class of things that could happen but that we can’t think of. In practice, there are many other distributional shifts, but RSA2048 is essentially the worst possible case of distributional shift, and I expect the solution to transfer pretty well.

This means that we can’t consider plans in which RSA2048 suddenly appears at some intermediate point. Note that this actually does still allow us to catch cases where the model merely does something bad the moment it sees RSA2048, because after we see RSA2048 in the real world during deployment, then we can actually just use that and plan through the consequences, and we’ll catch the treacherous turn there. So our failure case has to be subtler than that: the failures happen when there’s some action the agent can take that would make it such that our deploy time world model simulation thing breaks. Some examples:

The model self modifies to remove the world model simulator. This looks like a really good action, because removing this safeguard makes the model a lot more efficient, and because we can’t simulate worlds where RSA2048 happens, we don’t see it explode.
The model improves itself without removing the simulator but also in the process introduces some exploitable bugs (either intentionally or unintentionally).
If we prevent it from self modifying: The model creates a copy of itself that doesn’t have the safeguard.
If we also try to somehow prevent it from making new agents, there are a whole bunch of ways to goodhart whatever definition of agent we pick that could still put the world into a state where RSA2048 is bad

In general I don’t think we can make the model not take actions which would make it such that seeing RSA2048 would then cause bad things, though I admit to not having thought too much about it so I could be wrong.

The more general problem is that due to our world model being inaccurate, we can’t predict the consequences of the model’s actions accurately, and the model can exploit this to do things that are bad in ways we can’t think of. One corollary is the problem of always rejecting actions which do something bad that you can’t even understand—I also talked about this subproblem here. If you can do that, then you can reject everything that could potentially cause the world to enter into a state without the safeguards in ways you can’t understand, and of the remaining ones you should be able to understand them.

This problem actually applies to on-training-distribution things too. In the OOD frame, we kind of assume that on the training distribution we can simply tell on the training distribution whether it is indeed what we want, but in fact we can’t because to know whether we actually want it we would need to know the consequences of the action. In that sense, this frame is kind of orthogonal to the OOD one: OOD-only stuff is one problem, and the inability to see consequences is another orthogonal problem, but I think the latter is somewhat more fundamental because if we solve it then we can get (uncompetitive) OOD safety.

This also kind of ties into ELK: if we can solve ELK, then we can ask the model whether it thinks the action will lead to the safeguards being removed. The main problem here is that an action could still lead to the safeguards being removed even if the model doesn’t think so. An interesting avenue here would be how often this would happen—I don’t have much of a prior on even what order of magnitude problem this is. ELK might also simply not be solvable too, which makes this much more of a headache.

Future Directions: what do we do about actions that look good but are actually evil in ways that we can’t detect/comprehend; does ELK prevent safeguard removal in practice?

UPDATE: I made a followup post that dives into a bit more detail into the imperfect world modelling problem.