Four Levels of Voting Methods

Link post

This article presents four single-winner voting methods that are easy to understand and are a significant improvement over established voting systems. This also serves the secondary purpose of an introduction to voting theory, enabling an understanding of the motivation behind these methods, with no prior knowledge required. In particular I will present:

Approval voting—vote for all candidates you approve of
Score voting—score candidates on a scale
STAR voting—score candidates and have an automatic runoff between the best two
BTR-score—score candidates and have repeated runoffs between the worst two with the looser dropping out until only one remains

Introduction

Some people (who might have studied economics) don’t believe in $20 bills lying on the ground. If it were real, so the reasoning goes, someone would have already picked it up. Similarly, many people also don’t believe that we collectively might be doing something irrational and harmful, like hitting ourselves on the head with a stick, or building cars that can only turn left and right but never drive straight. This is how our current voting systems appear to someone who understands voting theory. My modest proposal is to stop hitting ourselves on the head with sticks.

There are many alternatives to the common choose-one voting system known as plurality voting (over 70 serious ones on my list). Ask some voting theory experts for the best single-winner voting method, and everyone will have their personal favorite. No one will choose plurality voting, but it is hard to tell (and there is no consensus) which one is the best. The reason is simple: judging by multiple metrics doesn’t guarantee one method will turn out to be the best in all of them. However, with multiple metrics, we can still have methods that are not strictly worse than others. This means, while some other method might be better in some metrics, none is better in all metrics. This is similar to the card game Top Trumps.

For real-world reform, I consider simplicity and accuracy the most important metrics. Simplicity is how hard it is to explain the method and the reason for choosing it to the average voter. It is crucial, because people have to understand the system to trust it.

Accuracy is measured, for example, in simulated elections as Voter Satisfaction Efficiency (VSE) Quinn, Huang. These simulations imagine a space with voters and candidates as points distributed along some axis. Voters are modeled to consider closer candidates more preferable. The simulation then compare the theoretical optimal outcome to those of various voting methods.

VSE (Huang) of various methods under “honest” and strategic assumptions.

A third important metric would be resistance to strategy, but it also correlates strongly with accuracy. To date, there exists no good measure for how simple a voting method is, but in most cases it’s easy to tell.

One result, right from the start: the common intuition that a more complicated method would also be more accurate is not always the case. There exist simple methods that perform very well (e.g. score) and more complicated ones that perform badly (e.g. Borda). When there is a method for which there is no other method that’s better in all criteria considered, it is called Pareto-optimal. The set of all data points for which this is true is the Pareto-front.

Illustration of how the space of voting methods can look like. With the Pareto-front marked in blue.

Please be aware that this graphic contains several subjective decisions, which is why I’m omitting labels. Most of all, with no objective measure of simplicity, the ordering here is entirely my personal assessment.

Voting theory knows many formal criteria, most of them dealing with what kinds of strategies are incentivized (both in voting and nomination) and what winner should be selected. For example, no favorite betrayal: “Is it always the best strategy to give the top vote to my favorite candidate?” Or Condorcet winner: “When there is a candidate that will beat everyone else in a runoff, are they guaranteed to win?” It can be mathematically proven if a method passes or fails such a criterion. These strict criteria have the problem that conforming to some desirable criteria excludes others. No favorite betrayal and Condorcet winner are mutually exclusive. We can’t have both at the same time. There is also no agreed-upon order on which are most important or which are wanted at all. The VSE simulations avoid this problem by looking at the result and by including different strategies. While there is room for improvement, they provide the most usable general measure for accuracy to date.

Four methods

Approval voting was first formally described and researched in the 1970s (but invented and used several times before), score in the 2000s, STAR was developed in 2014. BTR-score is a new invention and can be thought of as a variant of STAR, or Smith//score, which seems to date back to 2019.

This set of methods has the advantage that it is possible to explain them in a way that each voting method builds on the previous, reducing the total steps needed to understand each one. They also, very likely, are Pareto-optimal in simplicity and accuracy, or very close. Looking for a “better” method comes with a cost.

While more complexity doesn’t necessarily result in a more accurate method, there is a trade-off to be made. These four strike a balance between accuracy and complexity at different points along the spectrum. The improvements in accuracy have diminishing returns. High complexity can deter voters, so efforts to change public elections should be cautious about proposing complex methods solely because they are more accurate.

The problem: Plurality voting

Plurality voting is the one method everyone is familiar with. It’s the choose-one voting used in many places around the world. Yet, it has the worst VSE performance of all voting methods tested, only rivaled by Borda under strategic assumptions. The problem with plurality is far worse than just bad performance. Since every voter can only vote for one candidate, votes are like a limited resource that candidates compete over. This turns campaigning into a zero-sum game. Candidates with similar political values have to compete against each other. They split the votes, which benefits their mutual opponent. Because of this, so-called spoiler candidates are discouraged from running for election, and voters are incentivized to vote for the lesser of two evils. This reduces the available options and therefore the quality of the outcome. Political polarization is a result of the spoiler effect. This is a property of the voting method in particular, not (as often suggested) democracy in general.

Plurality voting can be thought of as splitting the electorate into competing, mutually exclusive, camps. The biggest group wins, even if they are an overall minority.

Approval voting

Approval voting is plurality voting without restrictions on how many candidates you can support.

Approval is the simplest of all (non-random) voting methods. It is a strong improvement on the usual choose-only-one style plurality voting with no downsides. It is even simpler than plurality because it removes the restriction of only voting for one candidate. Strategic considerations are also easier because there is no more incentive for dishonest strategy. The ballot looks familiar:

Approval voting ballot taken from starvoting.org with modifications.

Voters can approve as many candidates as they like. The most approved candidate wins.

It’s like using checkboxes instead of radio buttons on websites. Conceptually, approval voting can be seen as creating Venn diagrams of all voter preferences. The candidate with the most overlap represents the electorate the best.

The best strategy under approval voting is always an honest strategy. There is no incentive to lie about your preferences. An efficient way to vote is to identify the top two front runners, then approve the one you like better and everyone you prefer to them.

Approval voting with a runoff is used in the US cities of Fargo (North Dakota) and St. Louis (Missouri).

Score voting

Score voting is approval voting with intermediate values.

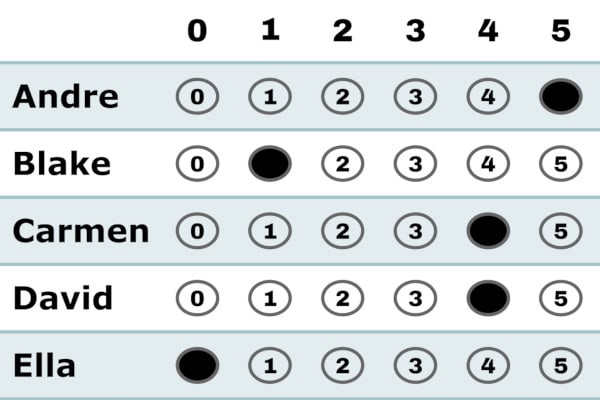
One criticism of approval is its binary nature. You either approve of a candidate or not. There is no option to differentiate. Score voting improves upon this by allowing in-between values, typically on a 0 to 5 or 0 to 9 scale.

Score voting ballot taken from starvoting.org with modifications.

Voters score candidates on a scale from 0 to 5. Blanks are counted as 0. The candidate with the highest total score wins.

When voters are modeled to have a utility function by which they assign each candidate a utility value (similar to the VSE simulations), then score voting is the theoretically optimal way to aggregate those preferences.

STAR voting

STAR voting is score voting with an automated runoff.

With score voting, an obvious (but not always beneficial) strategy is to exaggerate your preferences. You would give a maximum score to all candidates you want to win and zero to all others. If everyone does this, we lose some information and are at worst back to approval voting. Voters that don’t exaggerate to the extremes, but vote according to their true felt preference, may miss out on utilizing the full strength their ballot could have. STAR voting tries to counter this by introducing an automatic runoff round. Hence the acronym stands for “Score Then Automatic Runoff.” To the voters, the ballot looks the same as in score. However, in counting, we can extract more information than just the scores. A voter who gives candidate A 3 points and B 2 points obviously would prefer A over B in a runoff. We, therefore, can know pairwise preferences, and voters are incentivized to provide more information with intermediate values.

Voters score candidates on a scale from 0 to 5. Blanks are counted as 0. The two candidates with the highest total scores advance to the automatic runoff. Then all ballots are counted again regarding the pairwise preference of those two candidates. Ballots that score both the same are ignored. The candidate that is preferred on more ballots is elected.

STAR has a great advantage as many jurisdictions require a form of runoff or that the winner is elected with a formal majority. STAR provides this in one round of voting with a simple ballot and the accuracy and robustness of score voting.

The concept of “majority” is commonly misunderstood. Many people assume that a majority is the will of the electorate and everything that’s not a majority is not. There are a few misconceptions involved.

The concept of majority is only coherent in comparing two options, where voters can pick either one or the other. With more than two options, the resulting votes always depend on the voting method used and how the results are aggregated.
There might not be a majority even with two options. Voters can be indifferent and not vote either way. Forcing them to do so might in the worst case result in coin flipping in the voting booth.
A majority is a property of the electorate. If there is no majority in the electorate, then no voting method can guarantee a true majority.
Any voting method that “guarantees” a majority does so only on paper. Within certain conditions and looking at a subset of all votes, some majority can be found.
Given multiple options, there can be multiple majorities forming a cycle with no clear winner. See below for this Condorcet paradox.

BTR-score

BTR-score is STAR voting, but with runoffs for all candidates.

If in STAR voting two very similar candidates are at the top—say A and her twin sister A’ - then the runoff is only between those two—effectively turning it into plain score voting.

Now, what if we instead use the runoff method from STAR voting and use it on every possible pair of candidates? We then can make sure to elect the one candidate who would beat everyone else in a runoff. This concept is called a Condorcet method (as it is custom in science, named after the second person to discover it). There can be the rare case that there is no unique Condorcet winner to beat everyone else (probably less than 1%). Instead, there are three or more candidates trapped in a loop. Like rock paper scissors, A is preferred by a majority to B, B is preferred to C and C is preferred to A. In this case, we need a secondary metric to pick among these three. Luckily we already know about and have the necessary ballot information to use score voting for this.

By using a trick we can simplify the process and don’t have to compare every possible pair. To the voters, the ballot still looks the same as with score.

Voters score candidates on a scale from 0 to 5. Blanks are counted as 0. After counting the ballots, order the candidates from highest to lowest score. Compare the lowest two candidates by pairwise preference. The loser drops out, while the winner is compared to the next highest candidate. Repeat until only one candidate remains and therefore is elected.

This Bottom-Two-Runoff with score as ordering is the reason for the name BTR-score (pronounced “better score”).

While this method is not included in the VSE simulations mentioned above, it behaves very similarly to Smith//score. In fact, it gives exactly the same results unless there is a cycle of 4 or more candidates, which is theoretically possible, but exceedingly rare.

Analysis

Among voting theorists, there are roughly two philosophies about what kind of candidate should win an election. In simplified terms it can be summarized as score winner versus Condorcet winner. The score winner maximizes the utility of the electorate, while the Condorcet winner best represents the median voter. Note that those views have quite different textures. Utility is continuous and scores are given on an absolute scale, but the difference between candidates can take intermediary values. Condorcet methods, on the other hand, are discrete with relative comparisons; the preference between candidates is binary.

A big hindrance to the adoption of Condorcet methods is that most of them are quite complicated. It’s not enough to say “elect the candidate that would beat everyone else in a runoff”; it’s usually necessary to also explain the case of cycles and how to resolve them. BTR-score, as outlined here, is one of the simplest versions of such a method. Yet it still takes some explaining and the mental shift to see how rating a candidate can also give information about relative preferences.

With the four methods presented here, I don’t take a stance in that discussion but provide a view of how they can be compatible. It includes both kinds and hybrids in a common ballot format. From the perspective of Condorcet supporters, the other methods provide simpler stepping stones that ease the adoption of a Condorcet compliant method.

All four methods also share a desirable property, which I consider a minimal standard:

Voters can rate candidates independently of each other. This means, giving one candidate a full score does not prevent you from giving the same score to someone else. An obvious counterexample is plurality voting. In my opinion independence of ratings is essential because, when it is failed, candidates not only compete over winning the election but also over the votes. This would cause votes to be treated as a scarce resource which causes conflict (see the section on plurality voting). On the other hand, when passed, candidates can cooperate and voters are not limited to align with one group only.

What voting method should we use?

As stated in the beginning, I don’t want to claim that these are the best or only options. Instead, this collection is very practical in a particular sense as it provides several benefits at once. First, it builds up from simple to complex such that it is easier to understand each step and thereby reduces the additional complexity required to explain the next more accurate method. The question then simply becomes, what level of complexity can we tolerate? It also addresses potential criticism of each method without dismissing the argument or abandoning the method. To solve a particular problem, you have to switch to a more complex method—the criticism is valid, but solving it comes with a cost. At the same time, it establishes the concept of a Pareto-front of simplicity and accuracy for voting methods. By pointing out that none of these four methods is strictly better than the other, there is no need to fight over which is best. The ballot design is also the same, except for approval voting, which in turn looks just like the one most people are used to. All in all, it is a very compact and coherent toolbox for single-winner voting methods.