TLDR;

In previous work, we found a problematic form of feature splitting called “feature absorption” when analyzing Gemma Scope SAEs. We hypothesized that this was due to SAEs struggling to separate co-occurrence between features, but we did not prove this. In this post, we set up toy models where we can explicitly control feature representations and co-occurrence rates and show the following:

Feature absorption happens when features co-occur.
If co-occurring feature magnitudes vary relative to each other, we observe “partial absorption”, where a latent tracking a main feature sometimes fires weakly instead of not firing at all, but sometimes does fully not fire.
Feature absorption happens even with imperfect co-occurrence, depending on the strength of the sparsity penalty.
Tying the SAE encoder and decoder weights together solves feature absorption in toy models.

All code for this post can be seen in this Colab notebook.

The rest of this post will assume familiarity with Sparse Autoencoders (SAEs). But first, some background on feature absorption:

What is feature absorption?

Feature absorption is a problematic form of feature splitting where a SAE latent appears to track an interpretable concept, but actually has holes in its recall. Instead, other SAE latents fire on specific tokens and “absorb” the feature direction into approximately token-aligned latents.

For instance, in Gemma Scope SAEs we find a latent which seems to track the feature that a token “starts with S”. However, the latent will not fire on a few specific tokens that do start with S, like the token “short”.

In feature absorption, we find gerrymandered SAE latents which appear to track an interpretable concept but have holes in their recall. Here, we see the dashboard for Gemma Scope layer 3 16k, latent 6510 which appears to track “starts with S”, but mysteriously doesn’t fire on “_short”.

How is this different than traditional feature splitting?

In traditional feature splitting, we expect a more general latent to split into more specific latent, but still tracking the same concept and still interpretable. For instance, a “starts with L” latent might split into “starts with uppercase L” and “stats with lowercase L”. Theses more specific latents are still about starting with the letter L and nothing else, just more specific variants on it.

Traditional feature splitting doesn’t pose a problem for interpretability. In fact, it may even be desirable to be able to control how fine or corse grained a SAE’s latents are!

Feature absorption is different. In feature absorption, we end up with something like “Starts with L with a bunch of exceptions”, and then we get combo latents like “lion” which encode both “lionness” and “starts with L”.

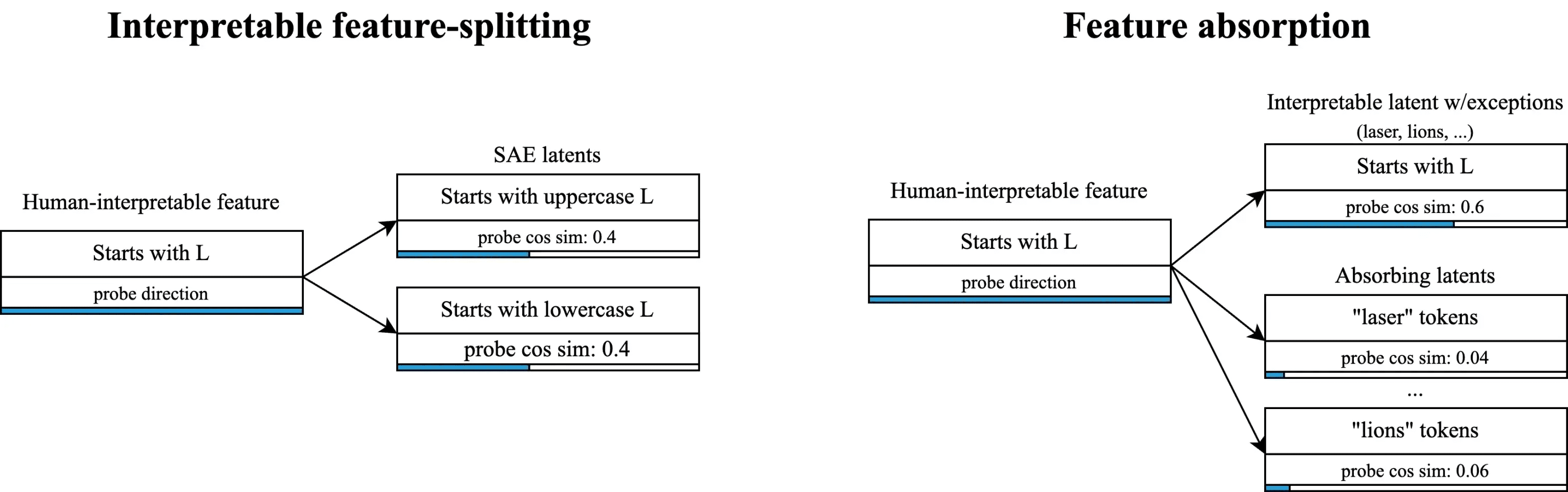
Feature absorption strictly reduces interpretability, and makes it hard to trust that a feature is doing what is appears to be doing. This is especially problematic when we don’t have ground truth labels, for instance if we’re trusting a latent tracking “deception” by the model. Furthermore, absorption makes it SAEs significantly less useful as an interpretability technique, because it means latent directions are spreading “true feature directions” across a number of unrelated latents.

Why does absorption happen?

We hypothesized that absorption is due to feature co-occurrence combined with the SAE maximizing sparsity. When two features co-occur, for instance “starts with S” and “short”, the SAE can increase sparsity by merging the “starts with S” feature direction into a latent tracking “short” and then simply not fire the main “start with S” latent. This means firing one feature instead of two! If you’re an SAE, this is a big win.

How big of a problem is this, really?

Our investigation implies that feature absorption will happen any time features co-occur. Unfortunately co-occurrence is probably the norm rather than the exception. It’s rare to encounter a concept that’s fully disconnected from all other concepts, and occurs completely independently of everything else. Any time we can say “X is Y” about concepts X and Y that means that there’s co-occurrence between these concepts. “dogs” are “animals”? co-occurrence. The “sky” is “blue”? co-occurrence. “3″ is a “number”? co-occurrence. In fact, it’s very difficult to think of any concept that doesn’t have any relation to another concept like this.

Toy Models of Feature Absorption Setup

Following the example of “Toy Models of Superposition” and “Sparse autoencoders find composed features in small toy models”, we want to put together a simple test environment where we can control everything going on to understand exactly under what conditions feature absorption happens. We have two setups, one without superposition and one with superposition.

Non-superposition setup

Our initial setup consists of 4 true features, each randomly initialized into orthogonal directions with a 50 dimensional representation vector and unit norm, so there is no superposition. We control the base firing rates of each of the 4 true features. Unless otherwise specified, the feature fires with magnitude 1.0 and stdev 0.0. We train a SAE with 4 latents to match the 4 true features using SAELens. The SAE uses L1 loss with coefficient 3e-5, and learning rate 3e-4. We train on 100,000,000 activations. Our 4 true features have the following firing rates:

	Feature 0	Feature 1	Feature 2	Feature 3
Firing rate	0.25	0.05	0.05	0.05

We use this setup for several reasons:

This is a very easy task for a SAE, and it should be able to reconstruct these features nearly perfectly.
Using fully orthogonal features lets us see exactly what the L1 loss term incentivizes to happen without worrying about interference from superposition.
This setup allows us to use exact same feature representations for each study in this post.

Regardless, most of these decisions are arbitrary, and we expect that the conclusions here should still hold for different choices of toy model setup.

Superposition setup

After we’ve demonstrated feature absorption in this simple setup and show that tying the SAE encoder and decoder together solves absorption, we then investigate the more complicated setup of superposition. In our superposition setup, we use 10 features each with a 9 dimensional representation. We randomly initialize these representations then optimize them to be as orthogonal as possible. We also increase the L1 loss term to 3e-2 as this seems to be necessary with more features in superposition. Otherwise, everything else is the same as in the non-superposition setup.

Perfect Reconstruction with Independent Features

When the true features fire independently, we find that the SAE is able to perfectly recover these features.

Above we see the cosine similarity between the true features and the learned encoder, and likewise with the true features and the decoder. The SAE learns one latent per true feature. The decoder representations perfectly match the true feature representations, and the encoder learns to perfectly segment out each feature from the other features. This is what we hope SAEs should do!

Feature co-occurrence causes absorption

Next, we modify the firing pattern of feature 1 so it fires only if feature 0 also fires. However, we keep the overall firing rate of feature 1 the same as before, firing in 5% of activations. Features 2 and 3 remain independent.

Here, we see a crystal clear example of feature absorption. Latent 0 has learned a perfect representation of feature 0, but the encoder has a hole in it! Latent 0 fires if feature 0 is active but not feature 1! This is exactly the sort of gerrymandered feature firing pattern we saw in Gemma Scope SAEs for the starting letter task—the encoder has learned to stop the latent firing on specific cases where it looks like it should be firing. In addition, we see that latent 3, which tracks feature 1, has absorbed the feature 0 direction! This results in latent 3 representing a combination of feature 0 and feature 1. We see that the independently firing features 2 and 3 are untouched—the SAE still learns perfect representations of these features.

We can see this absorption in some sample firing patterns below:

	True features				SAE Latents
	0	1	2	3	0	1	2	3
Sample input 1	1.00	0	0	0	0.99	0	0	0
Sample input 2	1.00	1.00	0	0	0	0	0	1.42
Sample input 3	0	0	1.00	0	0	0	1.00	0

Notably, only one SAE latent fires when both feature 0 and feature 1 are active.

Magnitude variance causes partial absorption

We next adjust the scenario above so that there is some variance in the firing magnitude of feature 0. We allow the firing magnitude to vary with a standard deviation of 0.1. In real LLMs, we expect that features will have some slight differences in their activation magnitudes depending on the context, so this should be a realistic adjustment.

Here we still see the characteristic signs of feature absorption: the latent tracking feature 0 has a clear hole in it for feature 1, and the latent tracking feature 1 has absorbed the representation of feature 0. However, the absorption in the decoder is slightly less strong that it was previously. Investigating some sample firing patterns, we see the following:

	True features
	0	1	2	3	1	2	3
Sample input 1	1.00	0	0	0	1.14	0	0
Sample input 2	1.00	1.00	0	0	0.20	0	1.37
Sample input 3	0.90	1.00	0	0	0.10	0	1.37
Sample input 4	0.75	1.00	0	0	0	0	1.37

Here when feature 0 and feature 1 both fire with magnitude 1.0, we see the latent tracking feature 0 still activates, but very weakly. If the magnitude of feature 0 drops to 0.75, the feature turns off completely.

We call this phenomemon partial absorption. In partial absorption, there’s co-occurrence between a dense and sparse feature, and the sparse feature absorbs the direction of the dense feature. However, the SAE latent tracking the dense feature still fires when both the dense and sparse feature are active, only very weakly. If the magnitude of the dense feature drops below some threshold, it stops firing entirely.

Why does partial absorption happen?

Feature absorption is an optimal strategy for minimizing the L1 loss and maximizing sparsity. However, when a SAE absorbs one latent into another, the absorbing latent loses the ability to modulate the magnitudes of the underlying features relative to each other. The SAE can address this by firing the latent tracking the dense feature as a “correction” to add back some of the dense feature direction into the reconstruction. Since the dense feature latent is firing weakly, it still has lower L1 loss than if the SAE fully separated out the features into their own latents.

Imperfect co-occurrence can still lead to absorption depending on L1 penalty

Next, let’s test what will happen if feature 1 is more likely to fire if feature 0 is active, but can still fire without feature 0. We set up feature 1 to co-occur with feature 0 95% of the time, but 5% of the time it can fire on its own.

Here we see the telltale markers of feature absorption, but they are notably reduced in magnitude relative to the examples above.

	True features				SAE Latents
	0	1	2	3	0	1	2	3
Sample input 1	1.00	0	0	0	0	0	1.00	0
Sample input 2	1.00	1.00	0	0	1.07	0	0.61	0
Sample input 3	0	1.00	0	0	0.93	0	0	0

Despite the slight signs of absorption, we see the SAE latent tracking feature 0 still does fire when feature 1 and feature 0 are active together, although with reduced magnitude. This still isn’t ideal as it means that the latents learned by the SAE don’t fully match the true feature representations, but at least the latents all fire when they should! But will this still hold if we increase the L1 penalty on the SAE?

Next, we increase the L1 coefficent from 5e-3 to 2e-2 and train a new SAE.

With this higher L1 coefficient, we see a much stronger feature absorption pattern in the encoder and decoder. Strangely, we also see the encoder for the latent tracking feature 1 encoding some of feature 0 - we don’t have an explanation of why that happens with partial co-occurrence. Regardless, let’s check the firing patterns for the SAE now:

	True features				SAE Latents
	0	1	2	3	0	1	2	3
Sample input 1	1.00	0	0	0	0	0.98	0	0
Sample input 2	1.00	1.00	0	0	1.40	0	0	0
Sample input 3	0	1.00	0	0	0.70	0	0	0

The firing patterns show feature absorption has occurred, where the latent tracking feature 0 fails to fire when both feature 0 and feature 1 are active. Here we see that the extent of the absorption increases as we increase our sparsity penalty. This makes sense as feature absorption is a sparsity-maximizing strategy for the SAE.

Tying the SAE encoder and decoder weights solves feature absorption

Looking at the patterns associated with absorption above, we always see a characteristic asymmetry between the SAE encoder and decoder. The SAE encoder creates a hole in the firing pattern of the dense co-occuring feature, but does not modify the decoder for that feature. Likewise, the absorbing feature encoder remains unchanged, but the decoder represents a combination of both co-occuring features. This points to a simple solution: what if we force the SAE encoder and decoder to share weights?

Amazingly, this simple fix seems to solve feature absorption! The SAE encoder and decoder learn the true feature representations! But this is a simple setup with no superposition; will this still work when we introduce more features and put them into superposition?

Absorption in superposition

To induce superposition, we now use a toy model with 10 features, each with a 9 dimensional representation. We then optimize these representations to be as orthogonal as possible, but there is still necessarily going to be overlap between feature representations. Below we show the cosine similarities between all true features in this setup. Features have about ±10% cosine similarity with all other features. This is actually more intense superposition than we would expect in a real LLM, but should thus be a good test!

Next, we create our original feature absorption setup except with 10 features instead of 4. Feature 0 has a 25% firing probability. Features 1-9 all have a 5% firing probability. Feature 1 can only fire if feature 0 fires. All features fire with magnitude 1.0. We also increase the L1 penalty to 3e-2, as this seems necessary given the superposition.

First, we try using our original SAE setup to verify that absorption still happens in superposition.

We still see the same characteristic absorption pattern between features 0 and 1. the encoder for the latent tracking feature 0 has a hole at feature 1, and the decoder for the latent tracking feature 1 represents a mix of feature 0 and 1 together. Interestingly, the encoder latent for feature 0 really emphasizes minimizing interference with features 2-9 in order to maximize the clarity of absorption! It’s like the SAE is priorititizing absorption over everything else.

Tying the encoder and decoder weights still solves feature absorption in superposition.

Next, we try tying together the SAE encoder and decoder weights while keeping the same absorption setup as before.

… And the SAE is still able to perfectly recover all feature representations, despite superposition! Hooray!

However this isn’t without downside—the MSE loss is no longer 0 as it was before superposition.

Future work

While tying the SAE encoder and decoder weights seems to solve feature absorption in the toy examples here, we haven’t yet tested this out on a non-toy SAE. It’s also likely that tying together the encoder and decoder will result in higher MSE loss, but there may be ways of mitigating this by using a loss term that encourages the encoder and decoder to be as similar as possible while allowing slight asymmetries between them, or fine-tuning the encoder separately in a second run. We also have not tried out this tied encoder / decoder setup on the combo feature toy model setup, so while this seems to fix absorption, it’s possible this solution may not help combo latent issues.

Another promising direction may be to try deconstructing SAEs into denser components using Meta SAEs, and building the SAE out of these meta-latents. It’s also likely there are more ways to solve absorption, such as adding an orthogonality loss or other novel loss terms, or constructing the SAE in other novel ways.

Acknowledgements

Thank you to LASR Labs for making the original feature absorption work possible!

Toy Models of Feature Absorption in SAEs