The Low-Hanging Fruit Prior and sloped valleys in the loss landscape
You can find code for the referenced experiments in this GitHub repository
Many have postulated that training large neural networks will enforce a simplicity, or Solomonoff prior. This is grounded in the idea that simpler solutions occupy expansive regions in the weight space (there exist more generalization directions in weight space along which loss does not increase or increases very little), translating to a broad attractor basin where perturbations in weight adjustments have a marginal impact on the loss.
However, stochastic gradient descent (SGD), the workhorse of deep learning optimization, operates in a manner that challenges this simplicity-centric view. SGD is, by design, driven by the immediate gradient on the current batch of data. The nature of this process means that SGD operates like a greedy heuristic search, progressively inching towards solutions that may be incrementally better but not necessarily the simplest.
Part of this process can be understood as a collection of “grokking” steps, or phase transitions, where the network learns and “solidifies” a new circuit corresponding to correctly identifying some relationships between weights (or, mathematically, finding a submanifold). This circuit then (often) remains “turned on” (i.e., this relationship between weights stays in force) throughout learning.
From the point of view of the loss landscape, this can be conceptualized as recursively finding a valley corresponding to a circuit, then executing search within that valley until it meets another valley (corresponding to discovering a second circuit), then executing search in the joint valley of the two found circuits, and so on. As the number of circuits learned starts to saturate the available weight parameters (in the underparametrized case), old circuits may get overwritten (i.e., the network may leave certain shallow valleys while pursuing new, deeper ones). However, in small models or models not trained to convergence, we observe that large-scale circuits associated with phase transitions largely survive to the end.
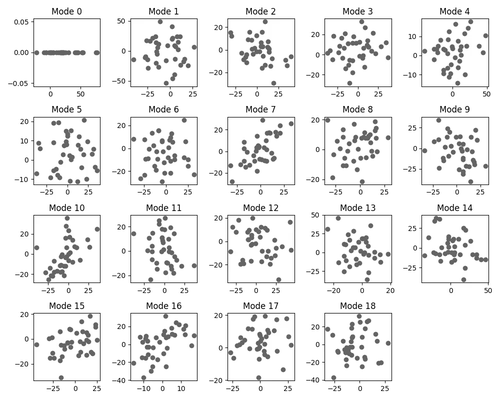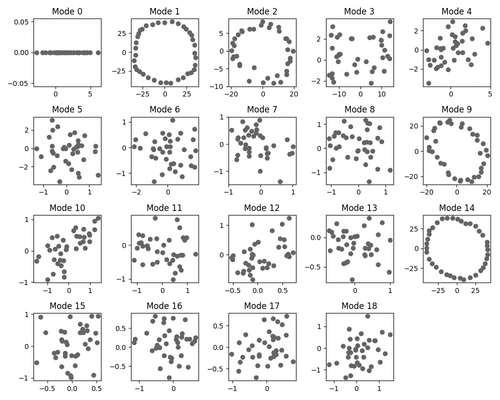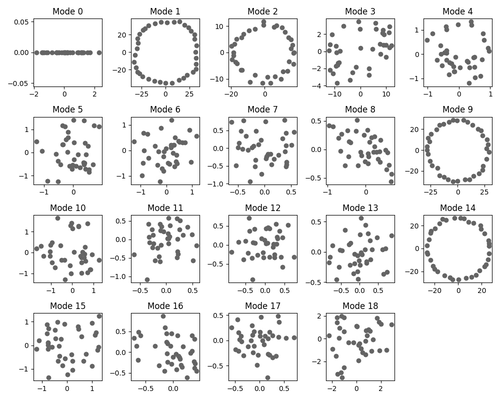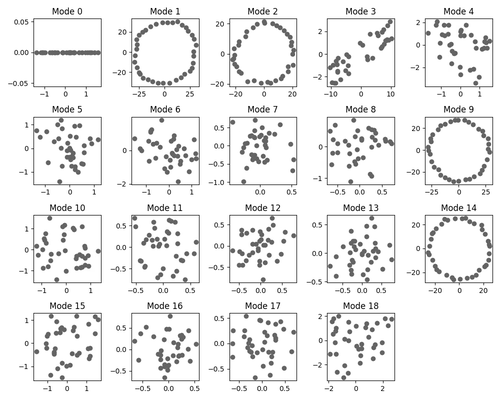
A greedier picture
This idea aligns with what we call the low-hanging fruit prior concept. Once a solution that reduces loss reasonably is identified, it becomes more computationally efficient to incrementally refine this existing strategy than to overhaul it in search of an entirely new solution, even if the latter might be simpler. This is analogous to continuously picking the lowest-hanging fruit / cheapest way to reduce loss at each stage of the gradient descent optimization search process.
This model predicts that SGD training processes are more likely to find solutions that look like combinations of shallow circuits and heuristics working together rather than simpler but less decomposable algorithms. In a mathematical abstraction, suppose that we have an algorithm that consists of two circuits, each of which requires getting parameters right (note that this corresponds to a measure of complexity), and each of which independently reduces the loss. Then the algorithm resulting from learning both circuits has a “complexity measure” of , but is more likely to be learned than a “complexity ” algorithm with the same loss if it cannot be learned sequentially (as it is exponentially harder to correctly “guess” 20 parameters than to correctly “guess” 10 parameters twice). Note that in general, the picture is more complicated: even when learning a single “atomic” circuit that cannot be further decomposed, the question of how easy it is to learn is not equivalent to the information content (how many parameters need to be learned), but incorporates more qualitative phenomena like basin shallowness or, more generally, local basin information similar to that studied by Singular Learning Theory—thus moving us even further away from the Solomonoff complexity prior.
An interesting consequence of this is a prediction that for tasks with two (or more) distinct ways to solve them, neural networks will tend to find or partially find both (or multiple) solutions, so long as the solutions have comparable complexity (in a suitable SGD sense). Our MNIST experiment (see below for details) confirms this: We design a network to solve a task with two possible solutions, one being a memorization task of patterns, and the other being the MNIST task of classifying digits; we set them up to have approximately the same effective dimension of (order of magnitude) 100. We observe that both are learned at comparable rates (and indeed, the part of the program classifying MNIST seems more stable). We conjecture that the network gradually learns independent bits of information from both learning problems by recursively picking the lowest-hanging fruit from both classification problems. I.e., by recursively finding the “easiest to learn” circuits that give additional usable information for the classification problem, and which may come from either memorization of patterns or learning the shapes of digits.
The idea of such a prior is not new. However, it is not sufficiently appreciated in AI safety circles how different this prior is from the simplicity prior: it gives a picture of a neural net as more akin to an ADHD child (seeking out new, “bite-sized” bits of information) than to a scientist trying to work out an elegant theory. Note that this does not imply a limit on the capabilities of current models: it is likely that by iterating on finding low-hanging fruit, modern networks can approach human levels of “depth.” However, this updates us towards expecting neural nets to have more of a preference for modularity and parallelism over depth.
Connection to the speed prior
In some discussions of priors, the Solomonoff prior is contrasted with the “speed prior.” The meaning of this prior is somewhat inconsistent: some take it to be associated with the KT complexity function (which is very similar to the Solomonov prior except for superexponential-time programs), and in other contexts, it is associated with properties of the algorithm the program is executing, such as depth. We think our low-hanging fruit prior is similar to the depth prior (and therefore also to speed priors that incorporate depth), as both privilege parallel programs. However, high parallelizability is not strictly necessary for a program to be learnable using a low-hanging fruit approach: it is possible that after enough parallel useful circuits are found, new sequential (and easily learnable) circuits can use the outputs of these parallel circuits to refine and improve accuracy, and a recursive application of this idea can potentially result in a highly sequential algorithm.
Modularity and phase transitions
Insights from experiments
In our experiments, we look at two neural nets with redundant generalization modules, i.e., networks where we can mechanistically check that the network is performing parallel subtasks that independently give information about the classification (which is then combined on a logit level). Our first network solves an image classification task which is a version of MNIST modified to have two explicitly redundant features that can be used to classify the image. Namely, we generate images that are a combination of two labeled datasets (“numbers” and “patterns”) with labels 0-9; these are combined in such a way that the number and the pattern on each image have the same label, and thus contain redundant information (the classification problem can be solved by looking at either feature).
We observe that the network naturally learns independent modules associated with the two classification tasks.
For our other test case, we reproduce a version of Neel Nanda’s modular addition transformer, which naturally learns multiple redundant circuits (associated with Fourier modes) that give complementary bits of information about a mathematical classification problem.
For both of these problems, we examine loss landscape basins near the solution found by the network, and we investigate how neural nets trained under SGD recursively find circuits and what this picture looks like “under a microscope” in the basin neighborhood of a local minimum with multiple generalizations.
Specifically, our experiments attempt to gain fine-grained information about a neural net and its circuits by considering models with smooth nonlinearities (in our case, primarily sigmoids). We train the network at a local minimum or near-minimum (found by SGD).
We then examine the resulting model’s basin in a coordinate-independent way on two levels of granularity:
1. Small neighborhood of the minimum: generalizations not distinguishable
In the small neighborhood (where empirically, the loss landscape is well-approximated by a quadratic function), we can associate to each generalization module a collection of directions (i.e., a vector space) in which this module gets generalized, but some other modules get ablated. For example, here is a graph of our steering experiment for the modified MNIST task:
It follows from our work that the composite network (red, “opacity 0.5”) executes two generalization circuits in the background, corresponding to reading “number” and “pattern” data.
In the right chart, we move a distance in the “number” generalization direction, ablating the “pattern” generalization. This results in very stable loss in the “number” circuit but non-negligible loss in the composite network.
The vectors we produce for extending one generalization while ablating the other results in almost no increase in loss for the generalization being preserved, high loss for the generalization being ablated, but (perhaps surprisingly) nonzero loss for the “joint” problem. The loss in the joint model is significantly (about an order of magnitude) less than the loss in the ablated circuit. However, it is far from being negligible.
In fact, it is not surprising that going in a generalization direction of one of the redundant modules does not result in flat loss since the information provided by the two modules is not truly “redundant.” We can see this in a toy calculation as follows.
Suppose that our two classification algorithms A, B attain an accuracy of 91% each by knowing with close to 100% certainty a subset of 90% of “easy” (for the given algorithm) patterns and randomly guessing on the remaining 10% of “hard” cases, and that, moreover, the easy and hard cases for the two algorithms are independent. Suppose that the logits for the “combined” algorithm are a sum of logits for the two constituent subalgorithms. In this case, we see that the constituent algorithms have cross-entropy loss of (associated with 10% accuracy in 10% of cases – the perfectly classified cases don’t contribute to loss). The “combined” network, now, will have perfect loss in 99% of cases (complement to the 1% of cases where both A and B don’t know the answer), and so the cross-entropy loss of the combined network is ; this picture, though a bit artificial, neatly explains the roughly order-of-magnitude improvement of loss we see in our MNIST model when both circuits are turned on compared to when only one circuit is turned on (as a result of steering).
In terms of generalization directions, the quadratic loss when steering towards a particular circuit is within the range of the top 10 or so eigenvalues of the Hessian, meaning that it is very strongly within the effective dimensionality of the task (which in the case of MNIST is of OOM 100). So in the model we consider, we see that looking at only one of the two features very much does not count as a generalization direction from the point of view of quadratic loss. Moreover, the generalization directions for the various circuits do not appear to be eigenvalues of the Hessian and look somewhat like “random” vectors with relatively high Hessian curvature.
2. Larger region where we can observe the ablation of a circuit: generalizations are “sloped canyons”
In a larger region with non-quadratic behavior, we find that the distinct generalizations correspond to lower-loss “canyons” within the loss landscape that are, in fact, local minima in all directions orthogonal to the vector connecting them to the minimum of the basin.
This confirms that the local geography of the loss landscape around models with multiple generalizations can look like a collection of sloped canyons converging towards a single basin. Near the basin is a “phase transition” phenomenon where the canyons stop being local minima and instead flow into a larger quadratic basin. A simplified version of the loss landscape looks like the following graph.
Relationship between “sloped canyons” model and low-hanging fruit prior
We note that this picture surprised us at first: we originally expected there to be a direction that generalizes one of the “redundant circuits” while not changing the loss.
Our updated picture of sloped canyons interfaces nicely with our sequential circuit formation prior. In situations where canyons are well-conceptualized as flat (like the picture) and correspond to a singular locus of minima, we would be less likely to expect sequential learning under SGD (as after learning one circuit, SGD would get “stuck” and stop moving towards the more general point near the origin), and in this picture, if networks learned more general solutions, we would expect this to happen mostly through many generalizations appearing at once (e.g., found by the diagonal gradient lines in the level set picture below).
What we observe in practice looks more like the following cartoon level set:
This picture is more consistent with learning one generalization at a time (here, the curved lines first get close to a coordinate axis – i.e., learn one redundant generalization, then descend to the joint generalization through SGD).
Having given cartoons for different generalization-learning patterns (either directly learning a general point or learning generalizations one at a time), we can informally compare the two hypotheses to dynamic captures of circuit formation under SGD for our modular addition algorithm. Interestingly, the pattern we see here seems to provide evidence for both mechanisms taking place. Indeed, while circuits do form sequentially, often, pairs or triples of circuits are learned at once or very close together:
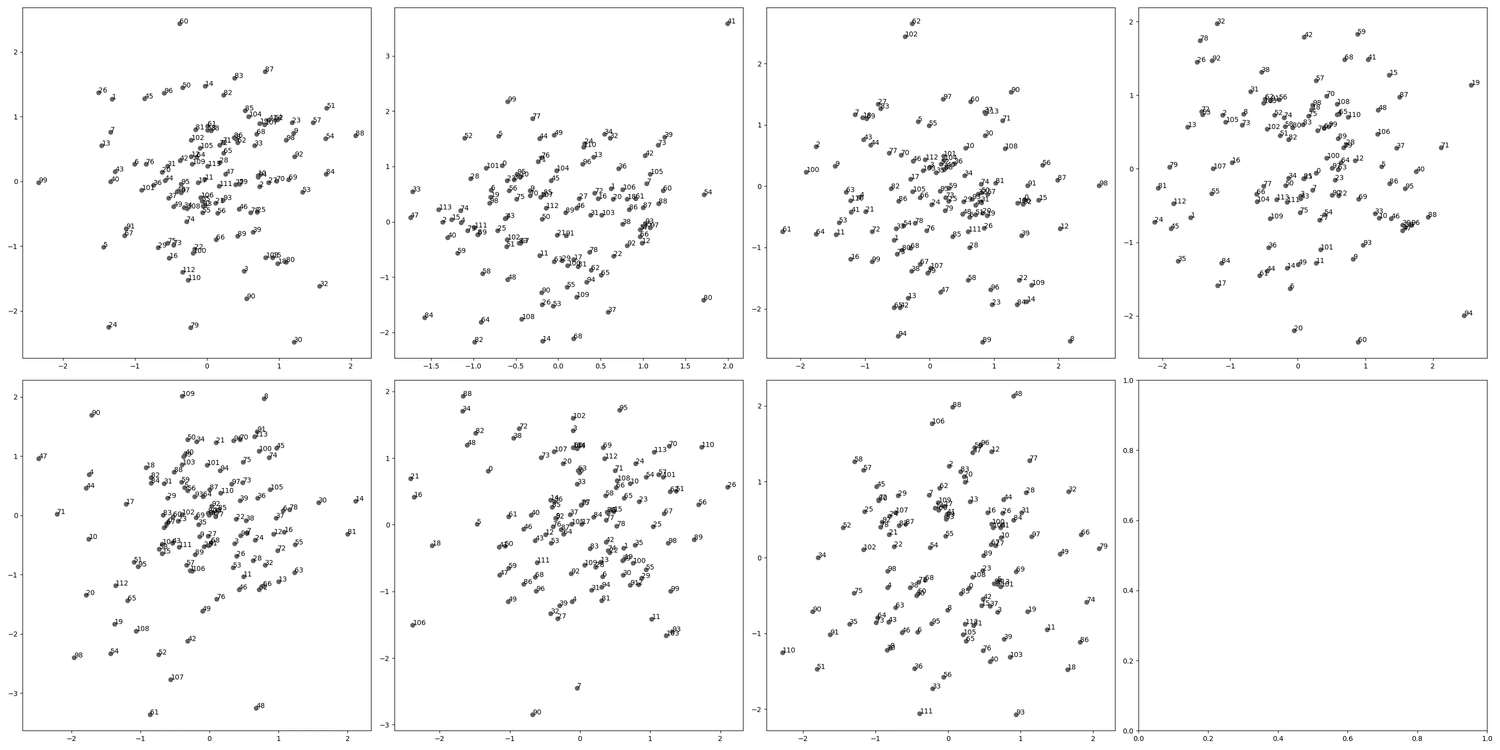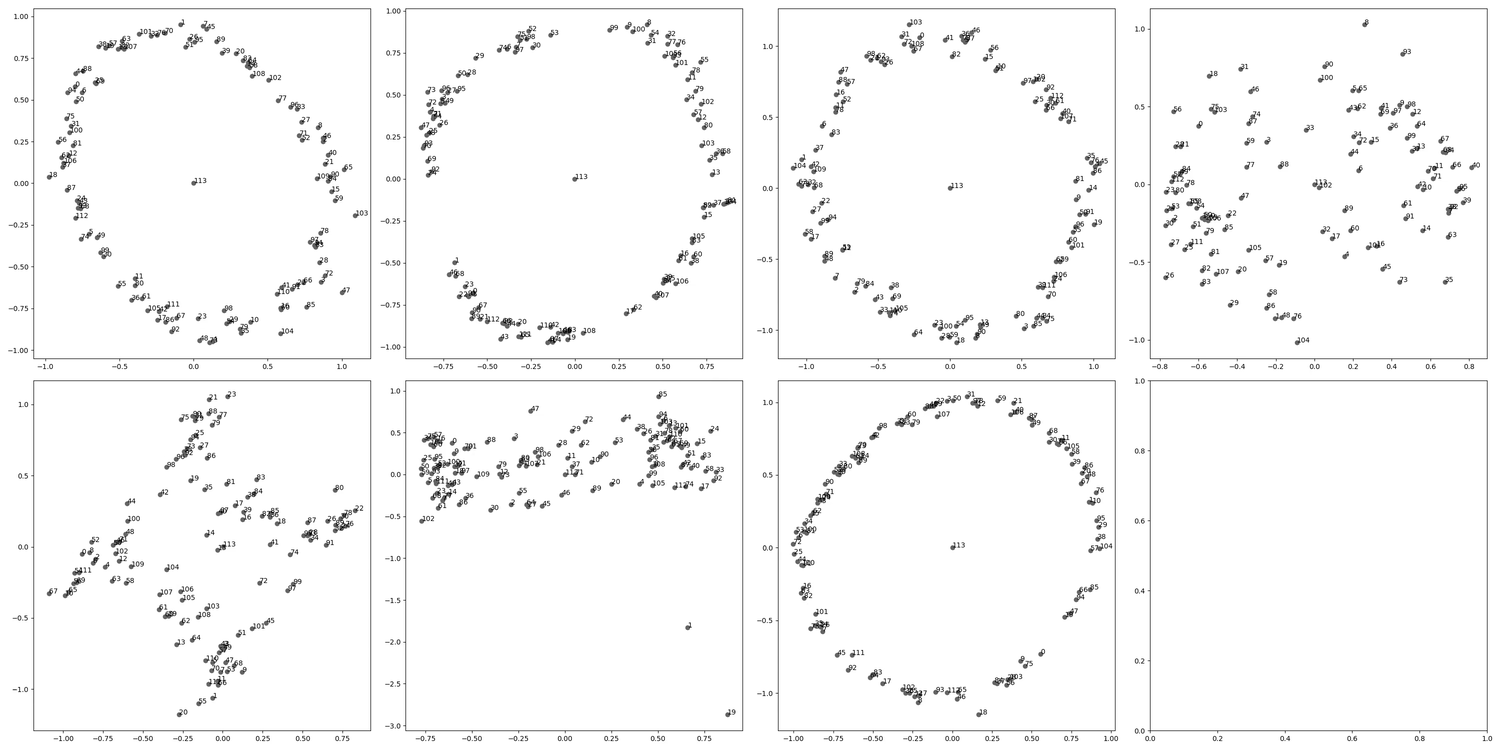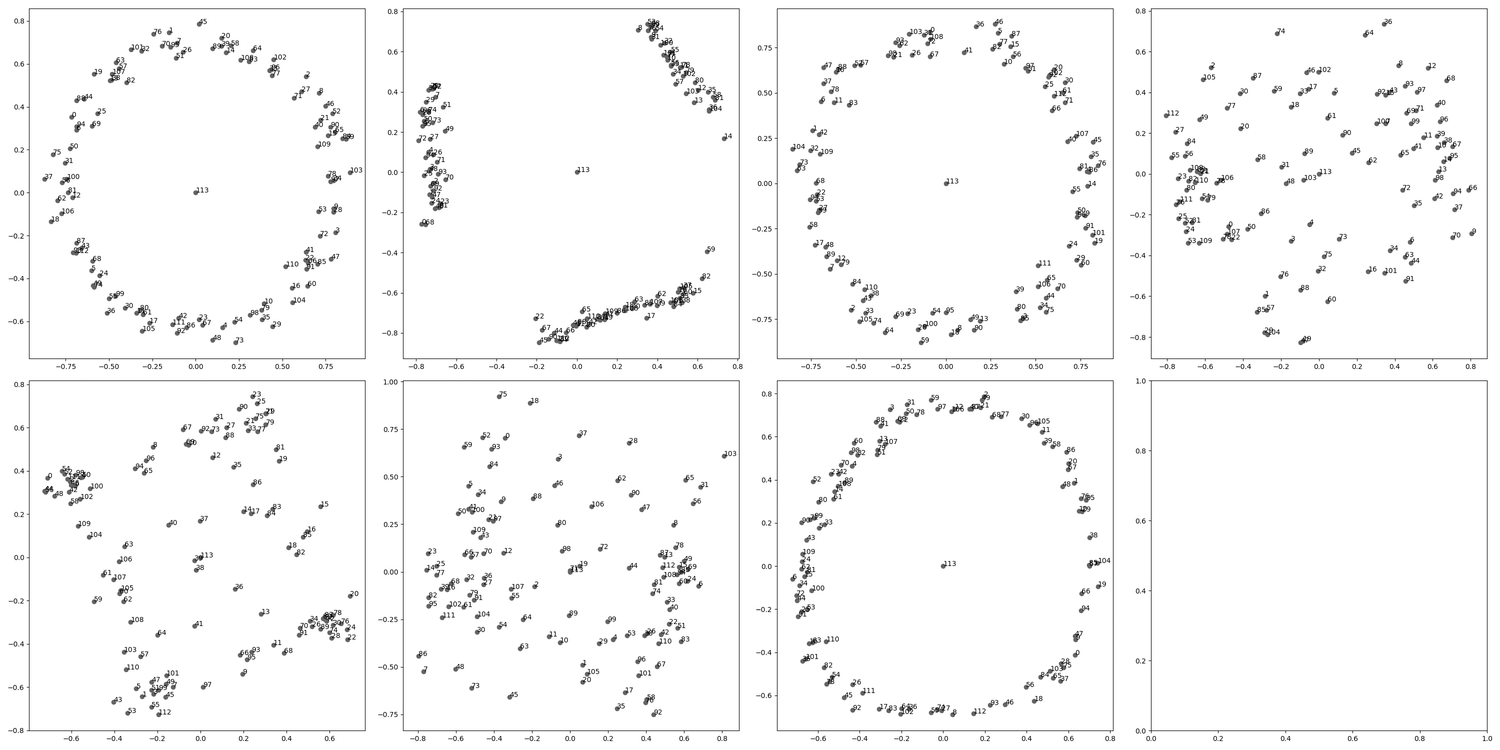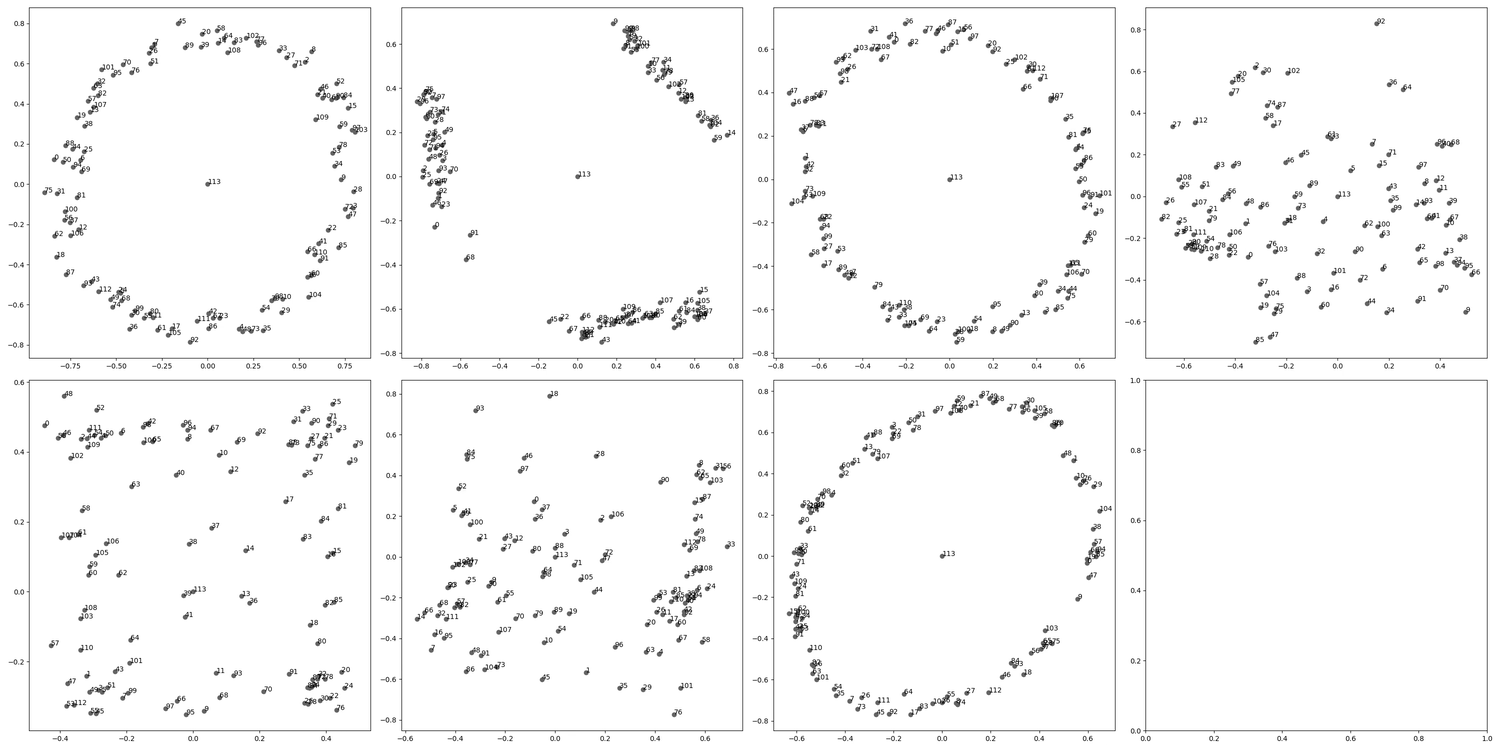
Note that a pure “greedy search” picture would predict that circuits form one by one according to a Poisson process, which would make this “pair formation” behavior unlikely, and somewhat complicates the sequential circuit formation picture. It would be interesting to do a more rigorous analysis of the stochastic behavior of circuit formation, though we have not done this at the moment. We expect explanations for these phenomena to have to do with a more detailed analysis of basins at various scale levels around the local minimum.
Acknowledgments
This write-up is part of research undertaken in the Summer 2023 SERI MATS program. We want to thank our mentor Evan Hubinger for useful discussions about speed and simplicity priors, and we want to thank Jesse Hoogland, Daniel Murfet, and Zach Furman for comments on an earlier version of this post.
- Circuits in Superposition: Compressing many small neural networks into one by (14 Oct 2024 13:06 UTC; 124 points)
- Grokking, memorization, and generalization — a discussion by (29 Oct 2023 23:17 UTC; 75 points)
- 's comment on Grokking, memorization, and generalization — a discussion by (31 Oct 2023 23:07 UTC; 2 points)
From a conversation on Discord:
Dmitry:
Response: