I didn’t adapt well. I am asthmatic, dyslexic, and, to make things worse, overwhelmed by the complexity of everything. I felt like information was flooding me, and I wasted my energy on improbable solutions.
Some people would say, “You need to be altruistic, help others.” Others said the opposite: “Think about yourself first; you need to take care of yourself before taking care of others.”
My problem might have been an overload of information, which created uncertainty. What seemed simple to others—“just do it”—for me was a series of unanswered questions:
What qualities should I have as a person?
What direction should I take?
How do I organize so much complexity?
I needed to reduce uncertainty. My solution came from an unexpected place: information entropy.
At one point in his life, Miyamoto Musashi sought not only to perfect his martial art but also to strengthen his body and mind through disciplined labor. To this end, he decided to cultivate a barren piece of land, believing that the process would refine his skills and sharpen his focus.
At first I tried to plant but the force of the water took almost a year’s work. Initially, Musashi attempted to control the flow of water on his land by building barriers to block it. However, each time the rains came, these barriers collapsed under the force of the water, leaving his efforts in ruins. He soon realized that resisting the natural flow was not only futile but also a waste of energy.
Determined to find a better solution, Musashi shifted his approach. Rather than fighting against the water, he observed its patterns and behaviors. He designed a simple but effective system of channels to guide the flow, distributing its force in a way that nourished the land instead of destroying it. This shift in mindset was transformative:
Adaptation over resistance: Musashi learned to work with the terrain, channeling the water in harmony with its natural tendencies.
Observation and strategy: By studying the dynamics of the water, he created a system that required less effort yet achieved greater results.
Collaboration: Inspired by his perseverance, neighbors joined the effort, teaching Musashi the value of collective strength in achieving goals.
These lessons extended far beyond agriculture. In combat, Musashi began to embody the principle of channeling force rather than resisting it. Instead of clashing directly with an opponent’s strength, he learned to redirect it, turning it to his advantage. This philosophy became a cornerstone of his fighting style, Niten Ichi-ryu, emphasizing control, adaptability, and strategy.
Through his failures and eventual success, Musashi discovered that true mastery—whether in battle or in life—comes not from imposing one’s will upon the world, but from understanding and working with its natural flows.
Imagine that your motivation is like water. Today, with constant overstimulation, floods often become too strong, stripping the soil of nutrients and sometimes even rotting the roots. Our instinctive response might be to build barriers to block it all out. But perhaps a solution lies in guiding that overstimulation, using its energy to create something sustainable.
To achieve this, we can start by dividing the overstimulation into two main channels:
One where the water can flow freely, inspiring you, nurturing natural expressions, and even lightly enriching the terrain of others.
Another that you can direct toward your personal land, channeling it to cultivate what truly matters to you.
This approach reflects what we outlined in previous texts: how to manage the flows of information and energy according to each individual’s “terrain”. At first I tried to plant but the force of the water took almost a year’s work. And now we are going to see how to organize it in levels, creating more specific functions of water use.
Once the water becomes more manageable, a deeper question arises: What is truly sustainable to plant with that motivation? Which actions deserve your investment, and how can they foster meaningful growth? What function can you assign to this terrain?
This text explores an ongoing project focused on generalizing personal actions and organizing them within your natural rhythm.
C) The Problem
In a world overwhelmed by information, cognitive biases, and constant comparisons, measuring personal growth becomes a daunting challenge.
D) Technical Introduction
Fundamentals: Entropy as a Starting Point Entropy, understood as the amount of uncertainty in a system, is the foundational concept of this model. Simply put, entropy measures how much unpredictable information exists. For example, when choosing a series to watch on Netflix, the greater the number of options, the higher the entropy: it becomes harder to make a clear decision.
Initial Premise:
Is there a variable more universal to human function than information?
Rooted in Maximum Entropy informational efficiency, we view the human being as a system that organizes, transforms, and propagates information—not as a passive physical body subject to chaos, but as an active agent refining its own informational processes. (Just as shadow doesn’t exist, only the absence of light, chaos doesn’t exist.)
The MaxEnt informational efficiency of a complex system is its ability to reorganize or generate useful information for itself (self‑updating) or for its environment (interaction), by maximizing subjective entropy under cognitive, contextual, or physiological constraints.
DNA and genetic diversity: A species with greater genetic diversity (more possible DNA configurations) has a higher probability of adapting and surviving environmental changes. The higher “entropy” in its genetic system gives it resilience against disruptions like diseases or climate shifts.
Another example:
Data redundancy in servers: A data system with multiple copies stored on different servers has more possible configurations to maintain the information if a failure occurs. The greater the number of states (backups), the higher the likelihood that the data will persist.
Premise: More individual order = Less individual entropy + More entropy for the universe.
Individual order and individual entropy
If “individual order” refers to reducing uncertainty within a system, this effectively implies lower entropy for that specific system.
Reducing individual entropy means imposing more constraints or certainties on the system’s possible states.
Impact on the universe
According to the second law of thermodynamics, any process that reduces entropy in a local system (individual order) leads to an increase in entropy in the surrounding system (the universe).
This is consistent because the energy required to order a local system dissipates as heat or disorder in the environment, increasing the universe’s entropy.
Provisional Conclusion: This aligns with thermodynamic principles, as long as the distinction between the local system (individual) and the global system (universe) is maintained.
Cleaning a room: When you tidy your room, you reduce the entropy of the local system (the room becomes more organized). However, the process generates disorder outside the system: you expend energy (burning calories), produce trash, or move clutter elsewhere. The total entropy of the universe increases.
Another example:
Freezing water: When water freezes, it becomes a more ordered system (ice has a crystalline structure). However, the energy released to the environment during the cooling process (heat) increases the global entropy.
Visualization:
States are the probable configurations of a system. A single stone has fewer probable states than a cockroach, for instance.
A stone has very few possible states: its configuration is simple and predictable (low entropy).
A living being, in contrast, has countless possible configurations, making it highly complex (high entropy).
In my case, the relationship between my capacity to process information and the amount of information I perceive from my environment is imbalanced. In mathematical terms: Processing Capacity < Information Perceived from the Environment → Higher Uncertainty.
Thus, my goal is to reduce uncertainty by creating more probable certainties in complex systems. The most effective tool I’ve found for this is Fermi Estimation.
The Fermi Method As a simplification technique based on estimation, the Fermi Method reduces uncertainty by making complexity manageable. This method, in addition to being intuitive, aligns with information theory: it simplifies complex systems into reasonable approximations.
High entropy: Visualize a chaotic cloud with random words, representing a disordered system.
Fermi Method: Divide that cloud into small, organized boxes that reveal clarity by breaking the problem into fragments.
The key to the model lies in applying the principles of information entropy within cognitive processes. In practice:
Break down uncertainty into manageable levels. By dividing a complex problem into simpler sub-problems, total entropy decreases.
Apply estimates to each level. This method forces us to simplify a situation by making logical, organized approximations.
Allocate energy optimally. Once uncertainty is divided and probable solutions are approximated, the next step is to prioritize cognitive resources where they will yield the greatest return.
We will explore each of these points in more detail in the following sections.
This approach does not aim to eliminate the world’s complexity but to make it manageable. Reducing personal entropy in my mind allows me to make better decisions, set clearer goals, and organize routines and tasks that are effective.
Applied Example: Using Fermi Estimation to Reduce Entropy Fermi Estimation is a powerful tool for simplifying complex systems and reducing uncertainty through logical approximations. It involves breaking a large problem into manageable factors, identifying the most relevant variables, and making reasonable assumptions using evidence and probabilistic thinking.
The Problem: How many piano tuners are there in Europe?
Step 1: Identify Key Variables The relevant variables are:
People
Professions
Piano tuners
Existing pianos
To reduce the initial complexity, I ask: Which variable holds the most information and is most accessible? Answer: People, as it is the variable with the most certainty. Additionally, each person can take on multiple roles: piano tuner, doctor, carpenter, etc. Thus:
Upper limit: Total population of Europe = 100%.
Step 2: Filter the Most Relevant Information Starting with 100% of people, I reduce entropy by identifying relevant subsets. I ask: What is the next largest variable to reduce uncertainty? Answer: Professions.
Let’s divide the population into two broad categories:
People engaged in technical tasks (environment construction).
People engaged in emotional tasks (human stimulation).
Evidence-based hypothesis: There is a higher demand for technical jobs in modern society. Therefore, I estimate a 2:1 ratio between technical and emotional roles:
Technical: 66%
Emotional: 33%
Step 3: Refine the Emotional Subset Within the 33% dedicated to emotional tasks, I identify three categories:
Visual artists
Performing artists
Auditory artists
With no evidence to prioritize one category, I divide them equally: 33% / 3 ≈ 11% in each category. Now:
People engaged in auditory tasks: 11% of the population.
Step 4: Identify Auditory Specialization Among those engaged in auditory tasks, I assume they focus on specific instruments:
Guitar
Piano
Voice
Violin
Double bass
With no evidence to prioritize one instrument, I divide equally: 11% / 5 ≈ 2.2%. The principle of maximum entropy suggests using uniform distribution when no additional information is available.
Thus:
People engaged in emotional work through the piano: 2.2% of the population.
Step 5: Determine the Proportion of Piano Tuners Not all individuals involved with the piano will be tuners. A tuner might work 8 hours per day, 6 days per week, servicing around 28 pianos weekly. If we assume that the 2.2% of the population involved with the piano requires tuning:
Divide 2.2% by the 28 clients per tuner.
Final Result: 0.07% of the European population could correspond to piano tuners.
Recommendations for Refining Solutions:
Seek data on:
Distribution of technical vs emotional professions.
Popularity of musical instruments (to refine the 11% / 5 division).
Frequency of piano tuning (e.g., once a year).
Incorporate new evidence to update estimates (Bayesian reasoning).
Conclusion Through this process, I reduced the initial uncertainty (100%) to a reasonable estimate: 0.07% of the European population. While it does not represent maximum precision due to a lack of complete data, it works excellently as an initial model! As shown below:
What moments of my life do I want to replicate?
Useful time that I can intentionally analyze to replicate
Initial Values: If I divide my daily routine:
~1/3 of the day sleeping.
~2/3 awake= 16.5% of total time
Step 1: Estimate Time in Functional States Let’s analyze my time awake. Over the past week:
Only 1⁄4 of this time, I was truly motivated to accomplish my goals.
Therefore: Useful time time that I c= 66% of total time.
Step 2: Refine Analysis for “Moments of Upper Motivation”
Of all my waking hours, what I aim to replicate are the moments of upper motivation. These are peak states where focus, drive, and engagement align to create optimal productivity and fulfillment. Identifying and analyzing the patterns that lead to these moments allows for intentional replication, supporting sustained well-being and effectiveness.
Of this motivated time, I estimate that only 1⁄8 was highly productive or deeply engaged.
Therefore: Highly motivated time = 2.06% of total time.
Conclusion from Calculations: By dividing my overall time into increasingly precise functional states, I reduced the initial uncertainty (100%) to a concrete estimation (2.06%). This process highlights where my energy is most effectively utilized and reveals areas for potential improvement.
F) Optimization of Well-Being States and Uncertainty Reduction
How can I sustain or enhance the states that reduce my uncertainty, bring me well-being, and increase the universe’s entropy?
Principles
1. Greater number of possible states → Higher probability of a data set persisting
2. More individual order → Less individual entropy + More entropy for the universe
3. Less individual entropy correlate with Moments of Upper Motivation
Empirical Foundations: Entropy and Well-Being
The connection between low local entropy states and subjective well-being is supported by several lines of research:
Neurobiological Basis
Efficient brain metabolism is linked to enhanced cognitive performance and emotional well-being (Magistretti & Allaman, 2015, Nature Reviews Neuroscience).
Neural network order, including reduced entropy in brain activity, correlates with positive mental states (Carhart-Harris et al., 2014, Frontiers in Human Neuroscience).
Metabolism and Optimal States
Flow states, described as optimal experiences, emerge under conditions of metabolic efficiency (Csikszentmihalyi, 1997, Flow: The Psychology of Optimal Experience).
Allostasis, the process of achieving stability through physiological change, supports psychological health and adaptive behavior (Sterling, 2012, Allostasis and the Brain).
Biological Systems and Order
Living systems thrive by maintaining order far from thermodynamic equilibrium, a principle central to life’s adaptive strategies (Schrödinger, 1944, What is Life?; Prigogine, 1984, Order Out of Chaos).
Energy efficiency and adaptability are predictors of resilience and well-being (Kauffman, 2000, Investigations).
Clinical Evidence
Disruptions in metabolic homeostasis are associated with mood disorders and cognitive decline (Raichle, 2015, Annual Review of Neuroscience).
Interventions optimizing metabolic balance, such as physical activity or nutritional adjustments, have been shown to improve subjective well-being (Wallace & Wallace, 2018, Origins of Life).
Reference Framework
The optimal state is defined as moments of peak motivation and well-being, established as the 100% benchmark. Achieving this state necessitates a strategic allocation of energy between personal growth and environmental engagement.
To quantify this, we use a model based on 100 daily energy units (100%). Systematic observation suggests a distribution where two-thirds of energy is dedicated to personal development, and one-third is allocated to interactions with the environment.
G) Filtering the Main Variables Through Entropy Limits
In a personal estimation model based on the Fermi Method, it is helpful to start by identifying the variables with the greatest influence on personal energy distribution. Among the many possibilities, the Elementary and Individual categories are particularly relevant because they offer clear and measurable boundaries.
1. Elementary Level (Ele):
These relationships can be narrowed down to the most basic and universal aspects of our energy and motivation.
Key Characteristics:
Rooted in genetic and environmental bases (Sapolsky, 2004; Miller et al., 2022).
Operate in a vegetative manner, maintaining basic functions without requiring specific stimuli (e.g., basal metabolism, respiration).
Highly predictable within a species and
governed by efficient self-regulation patterns, making them less costly in terms of adaptive energy (Friston, 2010, on the free energy principle).
Advantage for a Fermi Estimate: Because they are predictable and less context-dependent, these variables serve as a reliable anchor in the equation. Optimizing these relationships allows resources to be freed up for more demanding and complex processes.
2. Individual Level (Ind):
These relationships include the most adaptive and specific aspects of an individual, which develop through stimulus-response and memory.
We can define a limit, a boundary between Elemental reactions and Individual relationships when we use memory.
Key Characteristics:
Context-dependent and shaped by environmental interactions.
More variable and energy-intensive due to their adaptive nature.
Incorporate continuous learning and environmental processing to generate specific responses (Kahneman, 2011).
Advantage for a Fermi Estimate: Although these variables are less predictable, they more accurately reflect an individual’s adaptability and uniqueness. Mapping them allows for better model adjustments to personal conditions.
Why These Two Categories?
Elementary and Individual variables complement each other as axes of analysis:
Elementary relationships provide a reliable starting point for establishing baseline energy limits.
Individual relationships allow for fine-tuning the model, incorporating specific adaptations that reflect real human variability.
In terms of the Fermi Method, these categories function as key components for breaking down a complex system (our decisions and motivations) into more manageable and quantifiable parts, while ensuring a balance between stability (Ele) and flexibility (Ind).
Key References:
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers – on the interaction between genetics and environment.
Friston, K. (2010). The free-energy principle: A unified brain theory? – explains efficient self-regulation in biological systems.
Kahneman, D. (2011). Thinking, Fast and Slow – on context-dependent adaptive processes.
**Miller, R., & Smith, L. (2022). Energy distribution in adaptive systems – on energy in predictive and adaptive relationships.
Differentiation
Based on these characteristics, we can make a more precise differentiation in energy distribution, which will depend on the scenario and the individual. How much of my total elemental energy do I need to allocate to my individual process in life to achieve my Reference Moment of Upper Motivation?
Initial assumption remembering my life:
Ele.Ind = (2/3) = 66%
Visualizing Elemental/individual Processes in the Hierarchy
As shown in the figure below, we consider the individual process a subset of the elemental process. Not every individual process is Elemental, but every Individual process is Elemental.
Visual Summary of Energy Distribution
This analysis suggests a hierarchical energy distribution system consisting of:
Elementary Relationships: The foundational base of the system, representing 100% of the total.
Individual Relationships: Accounting for 66.67% of the total, as a more specific subset within the elementary system.
Key Considerations
Dynamic Energy Allocation:
Elementary energy does not follow a fixed percentage distribution.
Energy expenditure varies dynamically based on biological and contextual demands.
Process Interaction:
Biological systems do not strictly separate Elemental and Individual of information.
Energy is constantly redistributed between basic maintenance processes and adaptive interactions with the environment.
System Optimization:
This structure enables the optimization of both basic biological processes and adaptive environmental interactions.
However, refining individual variables (Ind) is crucial to improve precision in energy allocation and its impact on overall well-being.
3. Informacional Level (Inf)
Some beings, such as humans, use a significant portion of their energy for abstract information processing when they can compare memories.
With that, we can propose a boundary between individual relationships defined by the presence of relationships between memories. When interactions move beyond immediate stimulus-response and start integrating past experiences or memories to generate new insights, they transition into informational processes.
This transition enables:
What differentiates the behavior of an individual from a species.
Learning: Forming connections between past and present experiences.
Analysis: Comparing data, recognizing patterns, and deriving meaning.
Prediction: Using previous knowledge to anticipate future scenarios.
These processes reflect a higher-order energy allocation, focused on creating and refining meaning rather than merely reacting to the environment.
Personal Energy Allocation to Informational Processes
In my own life, I observe that many of my individual processes involve extensive memory integration (i.e., “thinking a lot”). Based on this, I estimate that at least 3⁄5 of my individual processes are informational in nature.
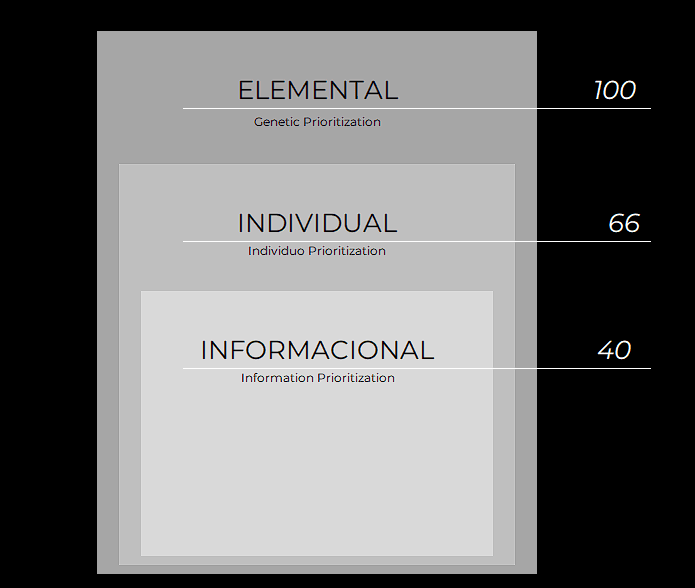
This results in: Ele.Ind.Inf = (2/3) * (3/5) = 40%.
Visualizing Informacional Processes in the Hierarchy
As illustrated in the figure below, the Informational Process is considered a subset of the Individual Process. While not every individual process is informational, every informational process is inherently individual.
.
Intellectual
These relationships encompass the most adaptive and specific aspects of an individual, emerging through the combination of memories.
Key Characteristics:
Context-dependent: Shaped by interactions with the environment, making them more variable and adaptive.
Memory-based: Extend beyond immediate reactions by integrating past experiences to form novel responses or insights.
Energy-intensive: Require significant resources due to the need for continuous learning and the processing of environmental information (Kahneman, 2011).
Informational Processes: When individual relationships involve deeper memory integration, they evolve into informational processes, focusing on higher-order functions such as learning, analysis, and prediction.
Advantage for a Fermi Estimate:
Although individual relationships are less predictable than elementary ones, their variability offers a more accurate reflection of adaptability and uniqueness. Identifying how much energy is allocated to Informational Processes (a subset of Individual Relationships) provides valuable insights for personal and model-based adjustments.
Why Include Informational Processes?
The distinction between Elementary, Individual, and Informational processes allows for a deeper understanding of energy distribution:
Elementary Relationships: Serve as a baseline, defining the lower energy limits for essential biological functions.
Individual Relationships: Enable fine-tuning by addressing adaptability and variability based on external stimuli on a memory.
Informational Processes: Represent the highest level of processing, where memory integration and abstract reasoning refine the adaptability introduced by individual relationships.
In the context of the Fermi Method, these three categories function together to simplify and quantify a complex system. Informational processes highlight the energy required for higher-order cognitive functions, offering a clearer path to optimizing both stability (Ele) and adaptability (Ind).
The analysis of energy distribution across Elementary, Individual, and Informational Relationships provides a structured framework for understanding how organisms allocate their resources to meet biological, adaptive, and cognitive demands. By distinguishing these categories:
Elementary Relationships serve as the foundation, maintaining essential functions with minimal adaptive energy.
Individual Relationships expand on this foundation, enabling adaptability through stimulus-response mechanisms and memory.
Informational Relationships elevate this adaptability to higher-order processes like learning, analysis, and prediction, requiring a more significant energy investment.
These categories work hierarchically, with Informational Processes forming the most energy-intensive subset of Individual Relationships. This hierarchical organization reflects the complexity of human energy allocation and underscores the necessity of refining energy expenditure for higher-order cognitive and adaptive tasks.
Key References:
Kahneman, D. (2011). Thinking, Fast and Slow: Highlights context-dependent adaptive processes and their energy demands.
Friston, K. (2010). The free-energy principle: A unified brain theory?: Explains efficient self-regulation in biological systems and the interaction of memory and prediction in adaptive processes.
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers: Provides insights on the role of stress and memory in shaping adaptive energy expenditure.
Miller, R., & Smith, L. (2022). Energy distribution in adaptive systems: Discusses energy allocation in predictive and adaptive relationships.
4. Social Level
Social relationships involve connecting information between individuals, sharing culture, and communication.
We can define a limit, a boundary between Informational relations and Social relations that is crossed when we use our informational processes to interact with other informational beings capable of combining their own memories.
Social relationships represent an additional layer of energy allocation where abstract reasoning, shared memory, and collaborative adaptation play crucial roles. They are particularly valuable for forming cohesive groups, fostering mutual understanding, and creating shared goals.
“Descartes’ Error” by Antonio Damasio is a highly relevant reference for this part of the text, particularly regarding social processes and the complexity of human behavior. Damasio effectively argues that Descartes was mistaken in separating the mind from the body and in considering purely rational processes as superior.
Your text presents a similar hierarchy of complexity:
Elementary Processes (more basic)
Individual Processes
Informational Processes
Social Processes (more complex)
This hierarchy aligns with Damasio’s perspective that:
Social processes are more complex than purely rational ones
Cognition is fundamentally tied to the body and emotions
Social processes require sophisticated integration of multiple systems (emotional, rational, bodily)
You could strengthen your theoretical framework by specifically incorporating:
Damasio’s idea that emotions and feelings are fundamental to rational decision-making
His emphasis on the embodied nature of cognition
His perspective on how social processes require an integration of systems that goes beyond pure reasoning
Personal Energy Allocation to Social Processes
In my own context, I observe that I dedicate more energy to Social Relationships than purely individual informational ones. I see that most of my active life was spent socializing. And my moment of maximum motivation was in a social interaction. I could say that 3⁄5 of my Information Processes are directed towards Social interactions, which leads to the following energy distribution:
Ele.Ind.Inf.Soc = (2/3) * (3/5) * (3/5) = 24%.
Visualizing Social Processes in the Hierarchy
This means that while all Social Relationships are rooted in informational processes, not every informational process necessarily evolves into a social one.
As illustrated in the figure below, the Social Process is considered a subset of the Informational Process. While not every informational process evolves into a social one, every social process is inherently informational.
Key Characteristics
Collaborative Memory Integration: Involves pooling individual memories and insights to create collective understanding.
Culture and Communication: Shared language, norms, and ideas facilitate the transfer and evolution of information.
Adaptive Advantage: Social bonds improve survival, reduce individual stress, and enhance motivation through group support.
Advantages for a Fermi Estimate
Social processes are inherently dynamic, varying based on group size, cultural context, and individual roles. Mapping the energy spent on these relationships provides critical insights into the balance between personal autonomy and group synergy. This distinction helps refine the model, allowing for an understanding of how social bonds influence overall well-being and motivation.
Why Include Social Processes?
Including Social Processes in the model allows for a deeper understanding of how energy is allocated in environments that require collaboration and communication. Social interactions build on informational exchanges, where individuals combine and share memories, ideas, and experiences. These interactions facilitate the formation of collective goals, shared motivations, and group dynamics, all of which are crucial for survival and adaptation in a social context. Social processes help optimize not only individual but also collective energy distribution, improving both personal and group-level decision-making, resilience, and problem-solving abilities.
Incorporating social processes into the energy distribution model underscores the significance of collaborative efforts in enhancing human potential. It recognizes the added value of shared knowledge, mutual influence, and social learning, which can amplify the adaptive capacities of individuals and groups.
Key References:
Damasio, A. R. (1994). Descartes’ Error: Emotion, Reason, and the Human Brain – Examines the interplay of emotion, reason, and embodiment in complex adaptive processes.
Kahneman, D. (2011). Thinking, Fast and Slow – Highlights how context-dependent adaptive processes shape human interactions and social behavior.
Friston, K. (2010). The Free-Energy Principle: A Unified Brain Theory? – Discusses the interaction of memory, prediction, and social learning in adaptive processes.
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers – Explores the role of stress and social dynamics in shaping adaptive energy expenditure.
Miller, R., & Smith, L. (2022). Energy Distribution in Adaptive Systems – Focuses on energy allocation within complex social and adaptive relationships.
IN/OUT ENERGY FRAMEWORK AS A PROCESS ORGANIZATION METHOD
Another method to evaluate motivation is to know the intention to change inside or outside.
The division of energy expenditure into internal modification (IN) and environmental interaction (OUT) processes offers a promising framework for process organization, supported by various research streams:
Neurobiological Evidence
Magistretti & Allaman’s (2015) work on brain metabolism demonstrates distinct energy patterns for internal processing versus environmental response
The Default Mode Network research shows clear delineation between internally-focused and externally-focused neural states (Raichle, 2015)
Psychological Research
Kahneman’s Dual Process Theory aligns with this division: System 2 (deliberate thinking) requiring more IN energy, while System 1 (automatic responses) operates more in the OUT domain
There are some interesting correlations:
System 1 (Automatic):
Tends to require more energy OUT
Lower individual entropy
Operates in states of higher metabolic efficiency
Aligns with the “moments of heightened motivation” mentioned
System 2 (Deliberate):
Requires more energy IN
Higher individual entropy during the process
Higher metabolic cost
Associated with periods of personal growth and learning
Flow state research (Csikszentmihalyi, 1997) indicates optimal performance occurs when IN/OUT energy allocation is appropriately balanced
Metabolic Studies
Sterling’s (2012) work on allostasis supports the concept of distinct energy allocations for internal regulation versus environmental adaptation
Wallace & Wallace (2018) demonstrate how metabolic efficiency correlates with clear IN/OUT energy distribution
Complex Systems Theory
Prigogine’s work (1984) on dissipative structures shows how living systems maintain order through distinct internal and external energy processes
Kauffman’s (2000) research on biological organization supports the necessity of differentiated energy allocation
Key Advantages of IN/OUT Framework:
Reference-Based Calibration
Uses personal peak performance states as calibration points
Allows for dynamic adjustment based on individual baseline states
Process Classification
Provides clear criteria for categorizing activities
Enables better resource allocation based on process type
Optimization Potential
Facilitates identification of energy inefficiencies
Supports strategic reallocation of resources
Individual Customization
Accommodates personal variations in energy distribution
Allows for context-specific adjustments
This framework’s strength lies in its ability to:
Use peak performance moments as reference points
Account for individual variations
Support dynamic energy allocation
Enable systematic process optimization
We could call these intentions to change Mega Vectors of action of an individual.
Personal MegaVector
In my personal state of Upper Motivation, how much do I need from each MegaVector to reach that state?
Total Energy = Energy to change oneself (IN) + Energy to change the environment (OUT) to my Moment of Upper Motivation?
Initial assumption remembering my life:
IN = 66.67% (or 2⁄3 of the total).
OUT = 33.33% (or 1⁄3 of the total).
*It would be more accurate to use variable ranges instead of fixed percentages.
Shown in the figure below, demonstrated in complementary positive axes, since negative entropy does not exist in the universe.
While variable ranges are often more precise for modeling complex systems, fixed percentages or reference points can be essential for providing clear and actionable estimations in practical scenarios. This allocation reflects a strategic focus on self-improvement while maintaining sufficient energy for external interactions.
Practical Examples
Personal Energy (IN): Optimizing dietary habits to boost energy levels, such as incorporating nutrient-dense meals that sustain focus and motivation throughout the day.
Environmental Energy (OUT): Enhancing workspace ergonomics for increased productivity, like adjusting lighting, minimizing distractions, and maintaining a clean, organized environment.
I don’t have extensive scientific references, and it would likely be more accurate to use variable ranges rather than fixed percentages. Each person’s observation of the energy or attention required by a system will vary depending on their goals and environment. However, this framework serves as a starting point that can be refined later.
Based on these characteristics, we can begin to differentiate energy distribution more precisely. While this approach is helpful, it remains too broad to dedicate equal time or focus to each variable. A more practical strategy would be to complement this with entropy limits, specifying ranges based on certain observable values.
By narrowing down entropy boundaries, we could create a more personalized and effective estimate, enabling us to allocate resources in a way that aligns better with individual needs and constraints. This refinement not only increases precision but also ensures that the model remains adaptable and relevant to unique contexts.
We can named this a MegaVectores
Results of the proportion of dedication for my Moment of Maximum Motivation considering MetaLevels by MegaVectors:
Categoría
IN (%)
OUT (%)
Total
66.67%
33.33%
Elemental
22.22%
11.11%
Elemental y Individual
44.44%
7.41%
Elemental y Individual y Informacional
26.67%
4.44%
Elemental y Individual y Informacional y Social
10.67%
1.07%
With that I can understand myself a little better and have a reference for:
Moments: Understanding upper and lower cognitive states.
Goals: Aligning aspirations with actionable plans.
Routines: Designing consistent structures for growth.
Tasks: Prioritizing actions based on cognitive readiness.
Through Personal Estimat Journals, you can track progress, iterate through self-experimentation, and evaluate decisions more effectively. This framework bridges theoretical insights with practical applications, paving a clear path toward self-optimization.
Conclusions
Mathematical formalization:
The model uses Bayesian updating implicitly
Initial quantification, while not perfect, allows for comparing states and making adjustments
Intuitive suggestions are a valid starting point that can be improved
Falsifiability:
The model is falsifiable through:
Tracking motivational states
Comparing predictions vs outcomes
Adjusting estimates based on observed outcomes
The key point seems to be: although the model is not perfect, it provides:
A structured initial framework
Capacity for refinement through evidence
Better approximation than no model at all
Basis for systematic improvements
Considerations
This analysis leads me to identify a refinement process based on four major categories:
Biological: Basic survival.
Individual: Personal adaptation.
Informational: Data processing and abstraction.
Social: Connection with other individuals.
I propose naming these categories MetaLevels of information within the individual, encompassing various levels of specialization. However, this framework is not as simplified as Fermi estimations, like the example of pianos mentioned in the text.
These MetaLevels could be divided by the MegaVectors—representing the intention to either change one’s internal system or alter the external environment. Additionally, we could further refine these into MacroVectors, which could be related to their evolutionary function. For inspiration and practical application, I will assign them evocative names, which I call PrimeIdentities.
In the next text, I will explore the importance of thinking about identities in a more abstract way, particularly in relation to personal motivation.
I call this ESTIMAT, a framework that combines the art of self-knowledge (“stimat”) with the science of life estimations (“estimat”).
Motivation Table
Meta Levels
Mega Vectors
Key Information to Evolutionary Biological Sense
MacroVectors
PrimeIdentities
Biological
in
I recognize, consume, ingest.
Store
Nurturer
I rest, store, and metabolize.
Recognize
Guardian
out
I discard, flee, inhibit.
Discard
Releaser
I act, fight, attack, and struggle.
Execute
Warrior
Individual
in
I highlight negative information, feel pain, observe errors.
Self-Observe
SelfSeer
I reduce errors and adapt stimuli.
Self-Transform
Versatile
out
I highlight positive information, feel pleasure.
Self-Motivate
Enthusiastic
I enhance successes and relate attitudes and ideas.
Self-Enjoy
Player
Informational
in
I review trends, ask if something could be false, analyze.
Analyze
Analyst
I predict what is most probable and create hypotheses.
Predict
Forecaster
out
I generalize, compare the easiest, fastest way.
Simplify
Synthesizer
I search, hunt, and trace.
Track
Tactician
Social
in
I empathize with what is important for others.
Empathize
Empathetic
I consider myself and the needs of as many people as possible, practicing effective altruism.
Deliberate
Altruistic
out
I help to understand, communicate.
Negotiate
Mediator
I communicate toward shared goals.
Cooperate
Partner
A another version
In the previous set illustrations, we considered the dependencies for each process to exist: the social process depends on processing information collectively, the informational process relies on individual memory, and the individual process requires the ancestral memory of the species. Now, we can visualize this in terms of the likelihood of generating more states in the universe, or entropy, which works in reverse: social processes are informational and group-based, so they have the highest potential for generating states. Informational processes, while individual, combine multiple individual memories, giving them more potential states than purely individual processes, which only relate individual memory to the environment. Finally, individual memories have a greater chance of generating states compared to species-level memories, which adapt more slowly.
H) Biases That Could Influence the Model
Confirmation Bias
Risk: We may be seeking examples that confirm our theory about Moments of Upper Motivation, while ignoring cases where the model does not work well.
Solution: Continuously refine the model with more organized and documented moments I search for a coaching.
Availability Bias
Risk: The prominent use 1 Moment of Upper Motivation might be overemphasized due to their vividness and memorability, while other valid contexts might be underrepresented.
Solution: Create a scientific journal to analyze new moments using the proposed framework.
Coherent Narrative Bias
Risk: We might be establishing causal connections where only correlations exist, simplifying complex mechanisms to create a “clean” story.
Solution: Constantly review the model and its applications in goals, routines, and tasks, avoiding hasty conclusions.
Hindsight Bias
Risk: While analyzing past motivational moments, we may reconstruct reasons that now seem more logical, distorting our memory of those states.
Solution: Although these reconstructions may be distorted, the important thing is that they motivate the user. With more moments documented systematically, we will filter biases through specific questions.
Generalization Bias
Risk: Personal experiences may be overgeneralized, and the model may not be universal across all contexts.
Solution: Recognize the limitations and test the model in various scenarios gradually, without expecting immediate results.
Optimism Bias
Risk: We might overestimate how easy it is to replicate these motivational states and the model’s effectiveness.
Solution: Accept that it is not easy; building these motivational states takes time and requires gradual adjustments.
I) Comparisons with Other Models
Model
Traditional Focus
Estimat Advantage
Maslow’s Hierarchy
Linear progression (needs → self-actualization).
Captures dynamic shifts between levels based on context.
Modern neuroscience integration; focuses on operational processes.
Cognitive Science Models
Isolated processes (e.g., memory, reasoning).
Hierarchical interplay between emotional, social, and intellectual systems.
Bayesian Brain Models
Probabilistic processing in isolation.
Adds a multilevel, hierarchical structure for prioritizing resources.
Gardner’s Intelligences
Discrete types of intelligence.
Explains how intelligence operates dynamically across levels.
Comparative Framework: Internal Family Systems, Coherence Therapy, and Bayesian Models in MetaFunctions
A comparative framework provides a simplified view of how Internal Family Systems (IFS), Coherence Therapy, and Bayesian Models integrate into the concept of MetaFunctions to address personal growth and sustainable transformation. Below is a table summarizing their key aspects:
Model
Core Concept
Integration with Estimat
Internal Family Systems (IFS)
The mind consists of internal “parts” (protectors, exiles) and a central Self that harmonizes them (Schwartz, 1995).
The Self acts as a MetaFunction coordinator, balancing emotional, social, and cognitive priorities to resolve internal conflicts.
Coherence Therapy
Persistent challenges stem from unconscious schemas coherent with past experiences (Ecker et al., 2012).
Aligns belief systems by addressing emotional coherence, freeing resources for higher-order goals through schema transformation.
Bayesian Models
Beliefs are updated probabilistically based on new evidence (Friston, 2010).
Enables dynamic prioritization and adaptation by applying probabilistic reasoning to allocate resources efficiently across contexts.
Unified Framework Highlights
IFS Contribution: Identifies and integrates internal agents (parts) within a dynamic system.
Coherence Therapy Contribution: Resolves conflicting schemas to align emotional and cognitive processes.
Bayesian Contribution: Enhances decision-making through iterative belief updates, ensuring adaptability and long-term optimization.
This table illustrates how each model contributes distinct yet complementary strengths to the overarching framework of Estimat, fostering a holistic approach to personal development.
This structured mapping ensures more clarity, helping you see how cognitive efforts at each level intersect with environmental demands.
A teacher working lesson might use a MetaFunction to anticipate potential distractions and plan engaging activities to keep students focused. Estimat has the potential to act as a “cognitive filter” to prioritize tasks and design solutions.
CONCLUSIONS
Much like how Miyamoto Musashi mastered the alignment of force and intention in his art, this framework harmonizes cognitive levels, transforming scattered efforts into a cohesive flow. By identifying probable MegaVector and MacroVector for flow—akin to planting seeds in fertile soil—we can cultivate environments where sustainable growth and motivation flourish.
This foundation lays the groundwork for a comprehensive map to estimate and deconstruct motivation, guided by key components:
Core Components:
MUM (Moments of Upper Motivation): Identifying and leveraging peak performance states
MetaLevels: Organizing cognitive inputs across different dimensions: Elemental, Individual, Informacional and Social
MegaVector: Mapping directional changes in motivation patterns: IN/OUT
MacroVector: Optimizing resource allocation for enhanced performance
PrimeIdentities: Framework for value-aligned decision-making
Key Applications:
Personal Analysis
Reduces cognitive biases and heuristic errors
Provides structured information theory-based analysis
Enables systematic tracking of motivational patterns
Practical Implementation
Maps daily energy distribution through MegaVectors
Analyzes recurring motivational patterns
Optimizes decision-making processes
Maximizes desired states while reducing uncertainty
Framework Validation The ESTIMAT system requires further empirical validation through:
Controlled simulations
Real-world testing
Data collection and analysis
Iterative refinement based on user feedback
This framework bridges theoretical concepts with practical applications, creating a systematic approach to personal development and motivation optimization. It offers a structured methodology for understanding and improving daily decision-making processes while maintaining flexibility for individual adaptation.
Join the Conversation!
What improvements would make this framework more actionable?
Are there specific challenges you’d like ESTIMAT to address?
Share your feedback and experiences with these concepts in your life.
Feel free to reach out for free coaching sessions and contribute to validating this framework. Your insights and experiences are invaluable in refining ESTIMAT into a practical and impactful tool.
Next Steps (Coming Soon):
Refine the conceptualization of each SuperFunction level as distinct vectors (biological, emotional, social, intellectual).
Expand research into Moments of Upper Motivation.
Develop techniques for grouping Moments of Upper Motivation by related MacroVectors.
Design strategies to mitigate cognitive bias.
Establish protocols for empirical validation.
Using ESTIMAT, we propose a framework to analyze and optimize:
Moments: Understanding upper and lower cognitive states.
Goals: Aligning aspirations with actionable plans.
Routines: Designing consistent structures for growth.
Tasks: Prioritizing actions based on cognitive readiness.
Through Personal Estimat Journals, you can track progress, iterate through self-experimentation, and evaluate decisions more effectively. This framework bridges theoretical insights with practical applications, paving a clear path toward self-optimization.
As this theory evolves, I’m excited to collaborate with you to build its empirical foundation and transform it into a practical tool for meaningful change. Together, we can shape a framework that empowers individuals to thrive in an age of overstimulation and complexity.
I’m Gabriel Brito, driven by a passion for self-stimat and self-estime. My work explores motivation by weaving together information theory and decision-making. Writing in English feels like a paraplegic playing for the major leagues—ambitious, awkward, and, every now and then, a miracle of technology.
References
Cognitive Load Theory: Sweller, J. (1988). Cognitive load during problem-solving: Effects on learning. (Explora cómo manejar la carga cognitiva mejora la toma de decisiones).
Entropy in Decision-Making: Research connecting Shannon entropy con la toma de decisiones y la gestión de incertidumbre.
Fermi Problems in Education: Artículos que demuestran cómo el Método de Fermi ayuda a simplificar problemas complejos.
MacLean, P. D. (1990). The Triune Brain in Evolution: Role in Paleocerebral Functions. Nueva York: Springer Science & Business Media.
About cognitive science models
Miller, G. A., Galanter, E., & Pribram, K. H. (1960). Plans and the Structure of Behavior. Nueva York: Holt, Rinehart and Winston.
Marr, D. (1982). Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. San Francisco: W.H. Freeman.
About cognitive science models
Knill, D. C., & Pouget, A. (2004). “The Bayesian Brain: The Role of Uncertainty in Neural Coding and Computation.” Trends in Neurosciences, 27(12), 712-719. https://doi.org/10.1016/j.tins.2004.10.007
On Gardner’s multiple intelligences
Gardner, H. (1983). Frames of Mind: The Theory of Multiple Intelligences. Nueva York: Basic Books.
About neuroscience and hierarchical levels
Damasio, A. R. (1994). Descartes’ Error: Emotion, Reason, and the Human Brain. New York: G.P. Putnam’s Sons.
Panksepp, J. (1998). Affective Neuroscience: The Foundations of Human and Animal Emotions. New York: Oxford University Press.
About decision-making models
Kahneman, D. (2011). Thinking, Fast and Slow. New York: Farrar, Straus and Giroux.
Tomasello, M. (2014). A Natural History of Human Thinking. Cambridge, MA: Harvard University Press.
Baumeister, R. F., & Leary, M. R. (1995). “The Need to Belong: Desire for Interpersonal Attachments as a Fundamental Human Motivation.” Psychological Bulletin, 117(3), 497-529. https://doi.org/10.1037/0033-2909.117.3.497
Satifaccion and Motivation Mapping through Information Theory
How channel motivation?
In this text, I propose a theoretical model for personal mapping based on information theory, Following These Steps
A) A Personal Contextualization of the Problem
B) Introducing the Problem Using Analogies
C) The Problem
D) Technical Introduction
E) How to Use Information Entropy to Prioritize Processes and Reduce Decision Uncertainty?
F) Optimization of Well-Being States and Uncertainty Reduction
G) Filtering the Main Variables Through Entropy Limits
H) Biases That Could Influence the Model
I) Comparisons with Other Models
References
A) A Personal Contextualization of the Problem
I didn’t adapt well. I am asthmatic, dyslexic, and, to make things worse, overwhelmed by the complexity of everything. I felt like information was flooding me, and I wasted my energy on improbable solutions.
Some people would say, “You need to be altruistic, help others.” Others said the opposite: “Think about yourself first; you need to take care of yourself before taking care of others.”
My problem might have been an overload of information, which created uncertainty. What seemed simple to others—“just do it”—for me was a series of unanswered questions:
What qualities should I have as a person?
What direction should I take?
How do I organize so much complexity?
I needed to reduce uncertainty. My solution came from an unexpected place: information entropy.
B) Framing the Problem with Analogies
At one point in his life, Miyamoto Musashi sought not only to perfect his martial art but also to strengthen his body and mind through disciplined labor. To this end, he decided to cultivate a barren piece of land, believing that the process would refine his skills and sharpen his focus.
At first I tried to plant but the force of the water took almost a year’s work. Initially, Musashi attempted to control the flow of water on his land by building barriers to block it. However, each time the rains came, these barriers collapsed under the force of the water, leaving his efforts in ruins. He soon realized that resisting the natural flow was not only futile but also a waste of energy.
Determined to find a better solution, Musashi shifted his approach. Rather than fighting against the water, he observed its patterns and behaviors. He designed a simple but effective system of channels to guide the flow, distributing its force in a way that nourished the land instead of destroying it. This shift in mindset was transformative:
Adaptation over resistance: Musashi learned to work with the terrain, channeling the water in harmony with its natural tendencies.
Observation and strategy: By studying the dynamics of the water, he created a system that required less effort yet achieved greater results.
Collaboration: Inspired by his perseverance, neighbors joined the effort, teaching Musashi the value of collective strength in achieving goals.
These lessons extended far beyond agriculture. In combat, Musashi began to embody the principle of channeling force rather than resisting it. Instead of clashing directly with an opponent’s strength, he learned to redirect it, turning it to his advantage. This philosophy became a cornerstone of his fighting style, Niten Ichi-ryu, emphasizing control, adaptability, and strategy.
Through his failures and eventual success, Musashi discovered that true mastery—whether in battle or in life—comes not from imposing one’s will upon the world, but from understanding and working with its natural flows.
Imagine that your motivation is like water. Today, with constant overstimulation, floods often become too strong, stripping the soil of nutrients and sometimes even rotting the roots. Our instinctive response might be to build barriers to block it all out. But perhaps a solution lies in guiding that overstimulation, using its energy to create something sustainable.
To achieve this, we can start by dividing the overstimulation into two main channels:
One where the water can flow freely, inspiring you, nurturing natural expressions, and even lightly enriching the terrain of others.
Another that you can direct toward your personal land, channeling it to cultivate what truly matters to you.
This approach reflects what we outlined in previous texts: how to manage the flows of information and energy according to each individual’s “terrain”. At first I tried to plant but the force of the water took almost a year’s work. And now we are going to see how to organize it in levels, creating more specific functions of water use.
Once the water becomes more manageable, a deeper question arises: What is truly sustainable to plant with that motivation? Which actions deserve your investment, and how can they foster meaningful growth? What function can you assign to this terrain?
This text explores an ongoing project focused on generalizing personal actions and organizing them within your natural rhythm.
C) The Problem
In a world overwhelmed by information, cognitive biases, and constant comparisons, measuring personal growth becomes a daunting challenge.
D) Technical Introduction
Fundamentals: Entropy as a Starting Point
Entropy, understood as the amount of uncertainty in a system, is the foundational concept of this model. Simply put, entropy measures how much unpredictable information exists. For example, when choosing a series to watch on Netflix, the greater the number of options, the higher the entropy: it becomes harder to make a clear decision.
Initial Premise:
Is there a variable more universal to human function than information?
Rooted in Maximum Entropy informational efficiency, we view the human being as a system that organizes, transforms, and propagates information—not as a passive physical body subject to chaos, but as an active agent refining its own informational processes. (Just as shadow doesn’t exist, only the absence of light, chaos doesn’t exist.)
DNA and genetic diversity:
A species with greater genetic diversity (more possible DNA configurations) has a higher probability of adapting and surviving environmental changes. The higher “entropy” in its genetic system gives it resilience against disruptions like diseases or climate shifts.
Another example:
Data redundancy in servers:
A data system with multiple copies stored on different servers has more possible configurations to maintain the information if a failure occurs. The greater the number of states (backups), the higher the likelihood that the data will persist.
Premise: More individual order = Less individual entropy + More entropy for the universe.
Individual order and individual entropy
If “individual order” refers to reducing uncertainty within a system, this effectively implies lower entropy for that specific system.
Reducing individual entropy means imposing more constraints or certainties on the system’s possible states.
Impact on the universe
According to the second law of thermodynamics, any process that reduces entropy in a local system (individual order) leads to an increase in entropy in the surrounding system (the universe).
This is consistent because the energy required to order a local system dissipates as heat or disorder in the environment, increasing the universe’s entropy.
Provisional Conclusion: This aligns with thermodynamic principles, as long as the distinction between the local system (individual) and the global system (universe) is maintained.
Cleaning a room:
When you tidy your room, you reduce the entropy of the local system (the room becomes more organized). However, the process generates disorder outside the system: you expend energy (burning calories), produce trash, or move clutter elsewhere. The total entropy of the universe increases.
Another example:
Freezing water:
When water freezes, it becomes a more ordered system (ice has a crystalline structure). However, the energy released to the environment during the cooling process (heat) increases the global entropy.
Visualization:
States are the probable configurations of a system. A single stone has fewer probable states than a cockroach, for instance.
A stone has very few possible states: its configuration is simple and predictable (low entropy).
A living being, in contrast, has countless possible configurations, making it highly complex (high entropy).
In my case, the relationship between my capacity to process information and the amount of information I perceive from my environment is imbalanced. In mathematical terms:
Processing Capacity < Information Perceived from the Environment → Higher Uncertainty.
Thus, my goal is to reduce uncertainty by creating more probable certainties in complex systems. The most effective tool I’ve found for this is Fermi Estimation.
The Fermi Method
As a simplification technique based on estimation, the Fermi Method reduces uncertainty by making complexity manageable. This method, in addition to being intuitive, aligns with information theory: it simplifies complex systems into reasonable approximations.
High entropy: Visualize a chaotic cloud with random words, representing a disordered system.
Fermi Method: Divide that cloud into small, organized boxes that reveal clarity by breaking the problem into fragments.
The key to the model lies in applying the principles of information entropy within cognitive processes. In practice:
Break down uncertainty into manageable levels.
By dividing a complex problem into simpler sub-problems, total entropy decreases.
Apply estimates to each level.
This method forces us to simplify a situation by making logical, organized approximations.
Allocate energy optimally.
Once uncertainty is divided and probable solutions are approximated, the next step is to prioritize cognitive resources where they will yield the greatest return.
We will explore each of these points in more detail in the following sections.
This approach does not aim to eliminate the world’s complexity but to make it manageable. Reducing personal entropy in my mind allows me to make better decisions, set clearer goals, and organize routines and tasks that are effective.
Applied Example: Using Fermi Estimation to Reduce Entropy
Fermi Estimation is a powerful tool for simplifying complex systems and reducing uncertainty through logical approximations. It involves breaking a large problem into manageable factors, identifying the most relevant variables, and making reasonable assumptions using evidence and probabilistic thinking.
The Problem:
How many piano tuners are there in Europe?
Step 1: Identify Key Variables
The relevant variables are:
People
Professions
Piano tuners
Existing pianos
To reduce the initial complexity, I ask:
Which variable holds the most information and is most accessible?
Answer: People, as it is the variable with the most certainty. Additionally, each person can take on multiple roles: piano tuner, doctor, carpenter, etc.
Thus:
Upper limit: Total population of Europe = 100%.
Step 2: Filter the Most Relevant Information
Starting with 100% of people, I reduce entropy by identifying relevant subsets. I ask:
What is the next largest variable to reduce uncertainty?
Answer: Professions.
Let’s divide the population into two broad categories:
People engaged in technical tasks (environment construction).
People engaged in emotional tasks (human stimulation).
Evidence-based hypothesis:
There is a higher demand for technical jobs in modern society. Therefore, I estimate a 2:1 ratio between technical and emotional roles:
Technical: 66%
Emotional: 33%
Step 3: Refine the Emotional Subset
Within the 33% dedicated to emotional tasks, I identify three categories:
Visual artists
Performing artists
Auditory artists
With no evidence to prioritize one category, I divide them equally:
33% / 3 ≈ 11% in each category.
Now:
People engaged in auditory tasks: 11% of the population.
Step 4: Identify Auditory Specialization
Among those engaged in auditory tasks, I assume they focus on specific instruments:
Guitar
Piano
Voice
Violin
Double bass
With no evidence to prioritize one instrument, I divide equally:
11% / 5 ≈ 2.2%.
The principle of maximum entropy suggests using uniform distribution when no additional information is available.
Thus:
People engaged in emotional work through the piano: 2.2% of the population.
Step 5: Determine the Proportion of Piano Tuners
Not all individuals involved with the piano will be tuners. A tuner might work 8 hours per day, 6 days per week, servicing around 28 pianos weekly.
If we assume that the 2.2% of the population involved with the piano requires tuning:
Divide 2.2% by the 28 clients per tuner.
Final Result:
0.07% of the European population could correspond to piano tuners.
Recommendations for Refining Solutions:
Seek data on:
Distribution of technical vs emotional professions.
Popularity of musical instruments (to refine the 11% / 5 division).
Frequency of piano tuning (e.g., once a year).
Incorporate new evidence to update estimates (Bayesian reasoning).
Conclusion
Through this process, I reduced the initial uncertainty (100%) to a reasonable estimate: 0.07% of the European population. While it does not represent maximum precision due to a lack of complete data, it works excellently as an initial model! As shown below:
What moments of my life do I want to replicate?
Useful time that I can intentionally analyze to replicate
Initial Values:
If I divide my daily routine:
~1/3 of the day sleeping.
~2/3 awake= 16.5% of total time
Step 1: Estimate Time in Functional States
Let’s analyze my time awake. Over the past week:
Only 1⁄4 of this time, I was truly motivated to accomplish my goals.
Therefore:
Useful time time that I c= 66% of total time.
Step 2: Refine Analysis for “Moments of Upper Motivation”
Of all my waking hours, what I aim to replicate are the moments of upper motivation. These are peak states where focus, drive, and engagement align to create optimal productivity and fulfillment. Identifying and analyzing the patterns that lead to these moments allows for intentional replication, supporting sustained well-being and effectiveness.
Of this motivated time, I estimate that only 1⁄8 was highly productive or deeply engaged.
Therefore:
Highly motivated time = 2.06% of total time.
Conclusion from Calculations:
By dividing my overall time into increasingly precise functional states, I reduced the initial uncertainty (100%) to a concrete estimation (2.06%). This process highlights where my energy is most effectively utilized and reveals areas for potential improvement.
F) Optimization of Well-Being States and Uncertainty Reduction
How can I sustain or enhance the states that reduce my uncertainty, bring me well-being, and increase the universe’s entropy?
Principles
1. Greater number of possible states → Higher probability of a data set persisting
2. More individual order → Less individual entropy + More entropy for the universe
3. Less individual entropy correlate with Moments of Upper Motivation
Empirical Foundations: Entropy and Well-Being
The connection between low local entropy states and subjective well-being is supported by several lines of research:
Neurobiological Basis
Efficient brain metabolism is linked to enhanced cognitive performance and emotional well-being (Magistretti & Allaman, 2015, Nature Reviews Neuroscience).
Neural network order, including reduced entropy in brain activity, correlates with positive mental states (Carhart-Harris et al., 2014, Frontiers in Human Neuroscience).
Metabolism and Optimal States
Flow states, described as optimal experiences, emerge under conditions of metabolic efficiency (Csikszentmihalyi, 1997, Flow: The Psychology of Optimal Experience).
Allostasis, the process of achieving stability through physiological change, supports psychological health and adaptive behavior (Sterling, 2012, Allostasis and the Brain).
Biological Systems and Order
Living systems thrive by maintaining order far from thermodynamic equilibrium, a principle central to life’s adaptive strategies (Schrödinger, 1944, What is Life?; Prigogine, 1984, Order Out of Chaos).
Energy efficiency and adaptability are predictors of resilience and well-being (Kauffman, 2000, Investigations).
Clinical Evidence
Disruptions in metabolic homeostasis are associated with mood disorders and cognitive decline (Raichle, 2015, Annual Review of Neuroscience).
Interventions optimizing metabolic balance, such as physical activity or nutritional adjustments, have been shown to improve subjective well-being (Wallace & Wallace, 2018, Origins of Life).
Reference Framework
The optimal state is defined as moments of peak motivation and well-being, established as the 100% benchmark. Achieving this state necessitates a strategic allocation of energy between personal growth and environmental engagement.
To quantify this, we use a model based on 100 daily energy units (100%). Systematic observation suggests a distribution where two-thirds of energy is dedicated to personal development, and one-third is allocated to interactions with the environment.
G) Filtering the Main Variables Through Entropy Limits
In a personal estimation model based on the Fermi Method, it is helpful to start by identifying the variables with the greatest influence on personal energy distribution. Among the many possibilities, the Elementary and Individual categories are particularly relevant because they offer clear and measurable boundaries.
1. Elementary Level (Ele):
These relationships can be narrowed down to the most basic and universal aspects of our energy and motivation.
Key Characteristics:
Rooted in genetic and environmental bases (Sapolsky, 2004; Miller et al., 2022).
Operate in a vegetative manner, maintaining basic functions without requiring specific stimuli (e.g., basal metabolism, respiration).
Highly predictable within a species and
governed by efficient self-regulation patterns, making them less costly in terms of adaptive energy (Friston, 2010, on the free energy principle).
Advantage for a Fermi Estimate:
Because they are predictable and less context-dependent, these variables serve as a reliable anchor in the equation. Optimizing these relationships allows resources to be freed up for more demanding and complex processes.
2. Individual Level (Ind):
These relationships include the most adaptive and specific aspects of an individual, which develop through stimulus-response and memory.
We can define a limit, a boundary between Elemental reactions and Individual relationships when we use memory.
Key Characteristics:
Context-dependent and shaped by environmental interactions.
More variable and energy-intensive due to their adaptive nature.
Incorporate continuous learning and environmental processing to generate specific responses (Kahneman, 2011).
Advantage for a Fermi Estimate:
Although these variables are less predictable, they more accurately reflect an individual’s adaptability and uniqueness. Mapping them allows for better model adjustments to personal conditions.
Why These Two Categories?
Elementary and Individual variables complement each other as axes of analysis:
Elementary relationships provide a reliable starting point for establishing baseline energy limits.
Individual relationships allow for fine-tuning the model, incorporating specific adaptations that reflect real human variability.
In terms of the Fermi Method, these categories function as key components for breaking down a complex system (our decisions and motivations) into more manageable and quantifiable parts, while ensuring a balance between stability (Ele) and flexibility (Ind).
Key References:
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers – on the interaction between genetics and environment.
Friston, K. (2010). The free-energy principle: A unified brain theory? – explains efficient self-regulation in biological systems.
Kahneman, D. (2011). Thinking, Fast and Slow – on context-dependent adaptive processes.
**Miller, R., & Smith, L. (2022). Energy distribution in adaptive systems – on energy in predictive and adaptive relationships.
Differentiation
Based on these characteristics, we can make a more precise differentiation in energy distribution, which will depend on the scenario and the individual. How much of my total elemental energy do I need to allocate to my individual process in life to achieve my Reference Moment of Upper Motivation?
Initial assumption remembering my life:
Ele.Ind = (2/3) = 66%
Visualizing Elemental/individual Processes in the Hierarchy
As shown in the figure below, we consider the individual process a subset of the elemental process. Not every individual process is Elemental, but every Individual process is Elemental.
Visual Summary of Energy Distribution
This analysis suggests a hierarchical energy distribution system consisting of:
Elementary Relationships: The foundational base of the system, representing 100% of the total.
Individual Relationships: Accounting for 66.67% of the total, as a more specific subset within the elementary system.
Key Considerations
Dynamic Energy Allocation:
Elementary energy does not follow a fixed percentage distribution.
Energy expenditure varies dynamically based on biological and contextual demands.
Process Interaction:
Biological systems do not strictly separate Elemental and Individual of information.
Energy is constantly redistributed between basic maintenance processes and adaptive interactions with the environment.
System Optimization:
This structure enables the optimization of both basic biological processes and adaptive environmental interactions.
However, refining individual variables (Ind) is crucial to improve precision in energy allocation and its impact on overall well-being.
3. Informacional Level (Inf)
Some beings, such as humans, use a significant portion of their energy for abstract information processing when they can compare memories.
With that, we can propose a boundary between individual relationships defined by the presence of relationships between memories. When interactions move beyond immediate stimulus-response and start integrating past experiences or memories to generate new insights, they transition into informational processes.
This transition enables:
What differentiates the behavior of an individual from a species.
Learning: Forming connections between past and present experiences.
Analysis: Comparing data, recognizing patterns, and deriving meaning.
Prediction: Using previous knowledge to anticipate future scenarios.
These processes reflect a higher-order energy allocation, focused on creating and refining meaning rather than merely reacting to the environment.
Personal Energy Allocation to Informational Processes
In my own life, I observe that many of my individual processes involve extensive memory integration (i.e., “thinking a lot”). Based on this, I estimate that at least 3⁄5 of my individual processes are informational in nature.
This results in:
Ele.Ind.Inf = (2/3) * (3/5) = 40%.
Visualizing Informacional Processes in the Hierarchy
As illustrated in the figure below, the Informational Process is considered a subset of the Individual Process. While not every individual process is informational, every informational process is inherently individual.
.

Intellectual
These relationships encompass the most adaptive and specific aspects of an individual, emerging through the combination of memories.
Key Characteristics:
Context-dependent: Shaped by interactions with the environment, making them more variable and adaptive.
Memory-based: Extend beyond immediate reactions by integrating past experiences to form novel responses or insights.
Energy-intensive: Require significant resources due to the need for continuous learning and the processing of environmental information (Kahneman, 2011).
Informational Processes: When individual relationships involve deeper memory integration, they evolve into informational processes, focusing on higher-order functions such as learning, analysis, and prediction.
Advantage for a Fermi Estimate:
Although individual relationships are less predictable than elementary ones, their variability offers a more accurate reflection of adaptability and uniqueness. Identifying how much energy is allocated to Informational Processes (a subset of Individual Relationships) provides valuable insights for personal and model-based adjustments.
Why Include Informational Processes?
The distinction between Elementary, Individual, and Informational processes allows for a deeper understanding of energy distribution:
Elementary Relationships: Serve as a baseline, defining the lower energy limits for essential biological functions.
Individual Relationships: Enable fine-tuning by addressing adaptability and variability based on external stimuli on a memory.
Informational Processes: Represent the highest level of processing, where memory integration and abstract reasoning refine the adaptability introduced by individual relationships.
In the context of the Fermi Method, these three categories function together to simplify and quantify a complex system. Informational processes highlight the energy required for higher-order cognitive functions, offering a clearer path to optimizing both stability (Ele) and adaptability (Ind).
The analysis of energy distribution across Elementary, Individual, and Informational Relationships provides a structured framework for understanding how organisms allocate their resources to meet biological, adaptive, and cognitive demands. By distinguishing these categories:
Elementary Relationships serve as the foundation, maintaining essential functions with minimal adaptive energy.
Individual Relationships expand on this foundation, enabling adaptability through stimulus-response mechanisms and memory.
Informational Relationships elevate this adaptability to higher-order processes like learning, analysis, and prediction, requiring a more significant energy investment.
These categories work hierarchically, with Informational Processes forming the most energy-intensive subset of Individual Relationships. This hierarchical organization reflects the complexity of human energy allocation and underscores the necessity of refining energy expenditure for higher-order cognitive and adaptive tasks.
Key References:
Kahneman, D. (2011). Thinking, Fast and Slow: Highlights context-dependent adaptive processes and their energy demands.
Friston, K. (2010). The free-energy principle: A unified brain theory?: Explains efficient self-regulation in biological systems and the interaction of memory and prediction in adaptive processes.
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers: Provides insights on the role of stress and memory in shaping adaptive energy expenditure.
Miller, R., & Smith, L. (2022). Energy distribution in adaptive systems: Discusses energy allocation in predictive and adaptive relationships.
4. Social Level
Social relationships involve connecting information between individuals, sharing culture, and communication.
We can define a limit, a boundary between Informational relations and Social relations that is crossed when we use our informational processes to interact with other informational beings capable of combining their own memories.
Social relationships represent an additional layer of energy allocation where abstract reasoning, shared memory, and collaborative adaptation play crucial roles. They are particularly valuable for forming cohesive groups, fostering mutual understanding, and creating shared goals.
“Descartes’ Error” by Antonio Damasio is a highly relevant reference for this part of the text, particularly regarding social processes and the complexity of human behavior. Damasio effectively argues that Descartes was mistaken in separating the mind from the body and in considering purely rational processes as superior.
Your text presents a similar hierarchy of complexity:
Elementary Processes (more basic)
Individual Processes
Informational Processes
Social Processes (more complex)
This hierarchy aligns with Damasio’s perspective that:
Social processes are more complex than purely rational ones
Cognition is fundamentally tied to the body and emotions
Social processes require sophisticated integration of multiple systems (emotional, rational, bodily)
You could strengthen your theoretical framework by specifically incorporating:
Damasio’s idea that emotions and feelings are fundamental to rational decision-making
His emphasis on the embodied nature of cognition
His perspective on how social processes require an integration of systems that goes beyond pure reasoning
Personal Energy Allocation to Social Processes
In my own context, I observe that I dedicate more energy to Social Relationships than purely individual informational ones. I see that most of my active life was spent socializing. And my moment of maximum motivation was in a social interaction. I could say that 3⁄5 of my Information Processes are directed towards Social interactions, which leads to the following energy distribution:
Ele.Ind.Inf.Soc = (2/3) * (3/5) * (3/5) = 24%.
Visualizing Social Processes in the Hierarchy
This means that while all Social Relationships are rooted in informational processes, not every informational process necessarily evolves into a social one.
As illustrated in the figure below, the Social Process is considered a subset of the Informational Process. While not every informational process evolves into a social one, every social process is inherently informational.
Key Characteristics
Collaborative Memory Integration: Involves pooling individual memories and insights to create collective understanding.
Culture and Communication: Shared language, norms, and ideas facilitate the transfer and evolution of information.
Adaptive Advantage: Social bonds improve survival, reduce individual stress, and enhance motivation through group support.
Advantages for a Fermi Estimate
Social processes are inherently dynamic, varying based on group size, cultural context, and individual roles. Mapping the energy spent on these relationships provides critical insights into the balance between personal autonomy and group synergy. This distinction helps refine the model, allowing for an understanding of how social bonds influence overall well-being and motivation.
Why Include Social Processes?
Including Social Processes in the model allows for a deeper understanding of how energy is allocated in environments that require collaboration and communication. Social interactions build on informational exchanges, where individuals combine and share memories, ideas, and experiences. These interactions facilitate the formation of collective goals, shared motivations, and group dynamics, all of which are crucial for survival and adaptation in a social context. Social processes help optimize not only individual but also collective energy distribution, improving both personal and group-level decision-making, resilience, and problem-solving abilities.
Incorporating social processes into the energy distribution model underscores the significance of collaborative efforts in enhancing human potential. It recognizes the added value of shared knowledge, mutual influence, and social learning, which can amplify the adaptive capacities of individuals and groups.
Key References:
Damasio, A. R. (1994). Descartes’ Error: Emotion, Reason, and the Human Brain – Examines the interplay of emotion, reason, and embodiment in complex adaptive processes.
Kahneman, D. (2011). Thinking, Fast and Slow – Highlights how context-dependent adaptive processes shape human interactions and social behavior.
Friston, K. (2010). The Free-Energy Principle: A Unified Brain Theory? – Discusses the interaction of memory, prediction, and social learning in adaptive processes.
Sapolsky, R. M. (2004). Why Zebras Don’t Get Ulcers – Explores the role of stress and social dynamics in shaping adaptive energy expenditure.
Miller, R., & Smith, L. (2022). Energy Distribution in Adaptive Systems – Focuses on energy allocation within complex social and adaptive relationships.
IN/OUT ENERGY FRAMEWORK AS A PROCESS ORGANIZATION METHOD
Another method to evaluate motivation is to know the intention to change inside or outside.
The division of energy expenditure into internal modification (IN) and environmental interaction (OUT) processes offers a promising framework for process organization, supported by various research streams:
Neurobiological Evidence
Magistretti & Allaman’s (2015) work on brain metabolism demonstrates distinct energy patterns for internal processing versus environmental response
The Default Mode Network research shows clear delineation between internally-focused and externally-focused neural states (Raichle, 2015)
Psychological Research
Kahneman’s Dual Process Theory aligns with this division: System 2 (deliberate thinking) requiring more IN energy, while System 1 (automatic responses) operates more in the OUT domain
There are some interesting correlations:
System 1 (Automatic):
Tends to require more energy OUT
Lower individual entropy
Operates in states of higher metabolic efficiency
Aligns with the “moments of heightened motivation” mentioned
System 2 (Deliberate):
Requires more energy IN
Higher individual entropy during the process
Higher metabolic cost
Associated with periods of personal growth and learning
Flow state research (Csikszentmihalyi, 1997) indicates optimal performance occurs when IN/OUT energy allocation is appropriately balanced
Metabolic Studies
Sterling’s (2012) work on allostasis supports the concept of distinct energy allocations for internal regulation versus environmental adaptation
Wallace & Wallace (2018) demonstrate how metabolic efficiency correlates with clear IN/OUT energy distribution
Complex Systems Theory
Prigogine’s work (1984) on dissipative structures shows how living systems maintain order through distinct internal and external energy processes
Kauffman’s (2000) research on biological organization supports the necessity of differentiated energy allocation
Key Advantages of IN/OUT Framework:
Reference-Based Calibration
Uses personal peak performance states as calibration points
Allows for dynamic adjustment based on individual baseline states
Process Classification
Provides clear criteria for categorizing activities
Enables better resource allocation based on process type
Optimization Potential
Facilitates identification of energy inefficiencies
Supports strategic reallocation of resources
Individual Customization
Accommodates personal variations in energy distribution
Allows for context-specific adjustments
This framework’s strength lies in its ability to:
Use peak performance moments as reference points
Account for individual variations
Support dynamic energy allocation
Enable systematic process optimization
We could call these intentions to change Mega Vectors of action of an individual.
Personal MegaVector
In my personal state of Upper Motivation, how much do I need from each MegaVector to reach that state?
Total Energy = Energy to change oneself (IN) + Energy to change the environment (OUT) to my Moment of Upper Motivation?
Initial assumption remembering my life:
IN = 66.67% (or 2⁄3 of the total).
OUT = 33.33% (or 1⁄3 of the total).
*It would be more accurate to use variable ranges instead of fixed percentages.
Shown in the figure below, demonstrated in complementary positive axes, since negative entropy does not exist in the universe.
While variable ranges are often more precise for modeling complex systems, fixed percentages or reference points can be essential for providing clear and actionable estimations in practical scenarios. This allocation reflects a strategic focus on self-improvement while maintaining sufficient energy for external interactions.
Practical Examples
Personal Energy (IN): Optimizing dietary habits to boost energy levels, such as incorporating nutrient-dense meals that sustain focus and motivation throughout the day.
Environmental Energy (OUT): Enhancing workspace ergonomics for increased productivity, like adjusting lighting, minimizing distractions, and maintaining a clean, organized environment.
I don’t have extensive scientific references, and it would likely be more accurate to use variable ranges rather than fixed percentages. Each person’s observation of the energy or attention required by a system will vary depending on their goals and environment. However, this framework serves as a starting point that can be refined later.
Based on these characteristics, we can begin to differentiate energy distribution more precisely. While this approach is helpful, it remains too broad to dedicate equal time or focus to each variable. A more practical strategy would be to complement this with entropy limits, specifying ranges based on certain observable values.
By narrowing down entropy boundaries, we could create a more personalized and effective estimate, enabling us to allocate resources in a way that aligns better with individual needs and constraints. This refinement not only increases precision but also ensures that the model remains adaptable and relevant to unique contexts.
We can named this a MegaVectores
Results of the proportion of dedication for my Moment of Maximum Motivation considering MetaLevels by MegaVectors:
Categoría
IN (%)
OUT (%)
Total
66.67%
33.33%
Elemental
22.22%
11.11%
Elemental y Individual
44.44%
7.41%
Elemental y Individual y Informacional
26.67%
4.44%
Elemental y Individual y Informacional y Social
10.67%
1.07%
With that I can understand myself a little better and have a reference for:
Moments: Understanding upper and lower cognitive states.
Goals: Aligning aspirations with actionable plans.
Routines: Designing consistent structures for growth.
Tasks: Prioritizing actions based on cognitive readiness.
Through Personal Estimat Journals, you can track progress, iterate through self-experimentation, and evaluate decisions more effectively. This framework bridges theoretical insights with practical applications, paving a clear path toward self-optimization.
Conclusions
Mathematical formalization:
The model uses Bayesian updating implicitly
Initial quantification, while not perfect, allows for comparing states and making adjustments
Intuitive suggestions are a valid starting point that can be improved
Falsifiability:
The model is falsifiable through:
Tracking motivational states
Comparing predictions vs outcomes
Adjusting estimates based on observed outcomes
The key point seems to be: although the model is not perfect, it provides:
A structured initial framework
Capacity for refinement through evidence
Better approximation than no model at all
Basis for systematic improvements
Considerations
This analysis leads me to identify a refinement process based on four major categories:
Biological: Basic survival.
Individual: Personal adaptation.
Informational: Data processing and abstraction.
Social: Connection with other individuals.
I propose naming these categories MetaLevels of information within the individual, encompassing various levels of specialization. However, this framework is not as simplified as Fermi estimations, like the example of pianos mentioned in the text.
These MetaLevels could be divided by the MegaVectors—representing the intention to either change one’s internal system or alter the external environment. Additionally, we could further refine these into MacroVectors, which could be related to their evolutionary function. For inspiration and practical application, I will assign them evocative names, which I call PrimeIdentities.
In the next text, I will explore the importance of thinking about identities in a more abstract way, particularly in relation to personal motivation.
I call this ESTIMAT, a framework that combines the art of self-knowledge (“stimat”) with the science of life estimations (“estimat”).
Motivation Table
Meta Levels
Mega Vectors
Key Information to Evolutionary Biological Sense
MacroVectors
PrimeIdentities
Biological
in
I recognize, consume, ingest.
Store
Nurturer
I rest, store, and metabolize.
Recognize
Guardian
out
I discard, flee, inhibit.
Discard
Releaser
I act, fight, attack, and struggle.
Execute
Warrior
Individual
in
I highlight negative information, feel pain, observe errors.
Self-Observe
SelfSeer
I reduce errors and adapt stimuli.
Self-Transform
Versatile
out
I highlight positive information, feel pleasure.
Self-Motivate
Enthusiastic
I enhance successes and relate attitudes and ideas.
Self-Enjoy
Player
Informational
in
I review trends, ask if something could be false, analyze.
Analyze
Analyst
I predict what is most probable and create hypotheses.
Predict
Forecaster
out
I generalize, compare the easiest, fastest way.
Simplify
Synthesizer
I search, hunt, and trace.
Track
Tactician
Social
in
I empathize with what is important for others.
Empathize
Empathetic
I consider myself and the needs of as many people as possible, practicing effective altruism.
Deliberate
Altruistic
out
I help to understand, communicate.
Negotiate
Mediator
I communicate toward shared goals.
Cooperate
Partner
A another version
H) Biases That Could Influence the Model
Confirmation Bias
Risk: We may be seeking examples that confirm our theory about Moments of Upper Motivation, while ignoring cases where the model does not work well.
Solution: Continuously refine the model with more organized and documented moments I search for a coaching.
Availability Bias
Risk: The prominent use 1 Moment of Upper Motivation might be overemphasized due to their vividness and memorability, while other valid contexts might be underrepresented.
Solution: Create a scientific journal to analyze new moments using the proposed framework.
Coherent Narrative Bias
Risk: We might be establishing causal connections where only correlations exist, simplifying complex mechanisms to create a “clean” story.
Solution: Constantly review the model and its applications in goals, routines, and tasks, avoiding hasty conclusions.
Hindsight Bias
Risk: While analyzing past motivational moments, we may reconstruct reasons that now seem more logical, distorting our memory of those states.
Solution: Although these reconstructions may be distorted, the important thing is that they motivate the user. With more moments documented systematically, we will filter biases through specific questions.
Generalization Bias
Risk: Personal experiences may be overgeneralized, and the model may not be universal across all contexts.
Solution: Recognize the limitations and test the model in various scenarios gradually, without expecting immediate results.
Optimism Bias
Risk: We might overestimate how easy it is to replicate these motivational states and the model’s effectiveness.
Solution: Accept that it is not easy; building these motivational states takes time and requires gradual adjustments.
I) Comparisons with Other Models
Model
Traditional Focus
Estimat Advantage
Maslow’s Hierarchy
Linear progression (needs → self-actualization).
Captures dynamic shifts between levels based on context.
Triune Brain (Evolution)
Sequential brain evolution (Reptilian → Limbic → Neocortex).
Modern neuroscience integration; focuses on operational processes.
Cognitive Science Models
Isolated processes (e.g., memory, reasoning).
Hierarchical interplay between emotional, social, and intellectual systems.
Bayesian Brain Models
Probabilistic processing in isolation.
Adds a multilevel, hierarchical structure for prioritizing resources.
Gardner’s Intelligences
Discrete types of intelligence.
Explains how intelligence operates dynamically across levels.
Comparative Framework: Internal Family Systems, Coherence Therapy, and Bayesian Models in MetaFunctions
A comparative framework provides a simplified view of how Internal Family Systems (IFS), Coherence Therapy, and Bayesian Models integrate into the concept of MetaFunctions to address personal growth and sustainable transformation. Below is a table summarizing their key aspects:
Model
Core Concept
Integration with Estimat
Internal Family Systems (IFS)
The mind consists of internal “parts” (protectors, exiles) and a central Self that harmonizes them (Schwartz, 1995).
The Self acts as a MetaFunction coordinator, balancing emotional, social, and cognitive priorities to resolve internal conflicts.
Coherence Therapy
Persistent challenges stem from unconscious schemas coherent with past experiences (Ecker et al., 2012).
Aligns belief systems by addressing emotional coherence, freeing resources for higher-order goals through schema transformation.
Bayesian Models
Beliefs are updated probabilistically based on new evidence (Friston, 2010).
Enables dynamic prioritization and adaptation by applying probabilistic reasoning to allocate resources efficiently across contexts.
Unified Framework Highlights
IFS Contribution: Identifies and integrates internal agents (parts) within a dynamic system.
Coherence Therapy Contribution: Resolves conflicting schemas to align emotional and cognitive processes.
Bayesian Contribution: Enhances decision-making through iterative belief updates, ensuring adaptability and long-term optimization.
This table illustrates how each model contributes distinct yet complementary strengths to the overarching framework of Estimat, fostering a holistic approach to personal development.
This structured mapping ensures more clarity, helping you see how cognitive efforts at each level intersect with environmental demands.
A teacher working lesson might use a MetaFunction to anticipate potential distractions and plan engaging activities to keep students focused. Estimat has the potential to act as a “cognitive filter” to prioritize tasks and design solutions.
CONCLUSIONS
Much like how Miyamoto Musashi mastered the alignment of force and intention in his art, this framework harmonizes cognitive levels, transforming scattered efforts into a cohesive flow. By identifying probable MegaVector and MacroVector for flow—akin to planting seeds in fertile soil—we can cultivate environments where sustainable growth and motivation flourish.
This foundation lays the groundwork for a comprehensive map to estimate and deconstruct motivation, guided by key components:
Core Components:
MUM (Moments of Upper Motivation): Identifying and leveraging peak performance states
MetaLevels: Organizing cognitive inputs across different dimensions: Elemental, Individual, Informacional and Social
MegaVector: Mapping directional changes in motivation patterns: IN/OUT
MacroVector: Optimizing resource allocation for enhanced performance
PrimeIdentities: Framework for value-aligned decision-making
Key Applications:
Personal Analysis
Reduces cognitive biases and heuristic errors
Provides structured information theory-based analysis
Enables systematic tracking of motivational patterns
Practical Implementation
Maps daily energy distribution through MegaVectors
Analyzes recurring motivational patterns
Optimizes decision-making processes
Maximizes desired states while reducing uncertainty
Framework Validation
The ESTIMAT system requires further empirical validation through:
Controlled simulations
Real-world testing
Data collection and analysis
Iterative refinement based on user feedback
This framework bridges theoretical concepts with practical applications, creating a systematic approach to personal development and motivation optimization. It offers a structured methodology for understanding and improving daily decision-making processes while maintaining flexibility for individual adaptation.
Join the Conversation!
What improvements would make this framework more actionable?
Are there specific challenges you’d like ESTIMAT to address?
Share your feedback and experiences with these concepts in your life.
Feel free to reach out for free coaching sessions and contribute to validating this framework. Your insights and experiences are invaluable in refining ESTIMAT into a practical and impactful tool.
Next Steps (Coming Soon):
Refine the conceptualization of each SuperFunction level as distinct vectors (biological, emotional, social, intellectual).
Expand research into Moments of Upper Motivation.
Develop techniques for grouping Moments of Upper Motivation by related MacroVectors.
Design strategies to mitigate cognitive bias.
Establish protocols for empirical validation.
Using ESTIMAT, we propose a framework to analyze and optimize:
Moments: Understanding upper and lower cognitive states.
Goals: Aligning aspirations with actionable plans.
Routines: Designing consistent structures for growth.
Tasks: Prioritizing actions based on cognitive readiness.
Through Personal Estimat Journals, you can track progress, iterate through self-experimentation, and evaluate decisions more effectively. This framework bridges theoretical insights with practical applications, paving a clear path toward self-optimization.
As this theory evolves, I’m excited to collaborate with you to build its empirical foundation and transform it into a practical tool for meaningful change. Together, we can shape a framework that empowers individuals to thrive in an age of overstimulation and complexity.
I’m Gabriel Brito, driven by a passion for self-stimat and self-estime. My work explores motivation by weaving together information theory and decision-making. Writing in English feels like a paraplegic playing for the major leagues—ambitious, awkward, and, every now and then, a miracle of technology.
References
Cognitive Load Theory: Sweller, J. (1988). Cognitive load during problem-solving: Effects on learning.
(Explora cómo manejar la carga cognitiva mejora la toma de decisiones).
Entropy in Decision-Making: Research connecting Shannon entropy con la toma de decisiones y la gestión de incertidumbre.
Fermi Problems in Education: Artículos que demuestran cómo el Método de Fermi ayuda a simplificar problemas complejos.
About Maslow’s hierarchy
Maslow, A. H. (1943). “A Theory of Human Motivation.” Psychological Review, 50(4), 370-396. https://doi.org/10.1037/h0054346
About the triune (evolutionary) brain
MacLean, P. D. (1990). The Triune Brain in Evolution: Role in Paleocerebral Functions. Nueva York: Springer Science & Business Media.
About cognitive science models
Miller, G. A., Galanter, E., & Pribram, K. H. (1960). Plans and the Structure of Behavior. Nueva York: Holt, Rinehart and Winston.
Marr, D. (1982). Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. San Francisco: W.H. Freeman.
About cognitive science models
Knill, D. C., & Pouget, A. (2004). “The Bayesian Brain: The Role of Uncertainty in Neural Coding and Computation.” Trends in Neurosciences, 27(12), 712-719. https://doi.org/10.1016/j.tins.2004.10.007
On Gardner’s multiple intelligences
Gardner, H. (1983). Frames of Mind: The Theory of Multiple Intelligences. Nueva York: Basic Books.
About neuroscience and hierarchical levels
Damasio, A. R. (1994). Descartes’ Error: Emotion, Reason, and the Human Brain. New York: G.P. Putnam’s Sons.
Panksepp, J. (1998). Affective Neuroscience: The Foundations of Human and Animal Emotions. New York: Oxford University Press.
About decision-making models
Kahneman, D. (2011). Thinking, Fast and Slow. New York: Farrar, Straus and Giroux.
Gigerenzer, G., & Gaissmaier, W. (2011). “Heuristic Decision Making.” Annual Review of Psychology, 62(1), 451-482. https://doi.org/10.1146/annurev-psych-120709-145346
About hierarchical and dynamic processes
Friston, K. (2010). “The Free-Energy Principle: A Unified Brain Theory?” Nature Reviews Neuroscience, 11(2), 127-138. https://doi.org/10.1038/nrn2787
Baddeley, A. (2000). “The Episodic Buffer: A New Component of Working Memory?” Trends in Cognitive Sciences, 4(11), 417-423. https://doi.org/10.1016/S1364-6613(00)01538-2
Regarding social interaction and cognitive levels
Tomasello, M. (2014). A Natural History of Human Thinking. Cambridge, MA: Harvard University Press.
Baumeister, R. F., & Leary, M. R. (1995). “The Need to Belong: Desire for Interpersonal Attachments as a Fundamental Human Motivation.” Psychological Bulletin, 117(3), 497-529. https://doi.org/10.1037/0033-2909.117.3.497