What we know about machine learning's replication crisis

Link post

The replication crisis is a a phenomenon that plagues modern day scientific research. And contrary to popular belief, it has being going on for a long time. The incentive structure within academia seems to reward quantity of publications over quality. This leads to questionable research practices which in turn lead to scientific journals containing false positive results.

This crisis is particularly strong in the social sciences where according to some estimates as much as 50% of published research is not replicable. The crisis is so prevalent in psychology that some psycholgists such as Daniel Lakens or Ulrich Schimmack made replication their main research interest.

But this is a blog about AI and machine learning, so what we’re interested in is knowing how robust the machine learning academic literature is. Does it suffer from this crisis ? Yes, it does. And according to computer science researcher Genevera Allen machine learning is also contributing to the replication crisis in other disciplines. She adds that she knows of the crisis from anecdotal evidence but does not have any number estimate of the proportion of reproducible (replicable and reproducible don’t mean the same thing but they are tightly linked and are part of the same problem) machine learning papers. In this article, we will review the existing literature and gather several strands of evidence of the replication crisis in machine learning and see if it is possible to get a number estimate.

Peer review in machine learning

Peer review is an integral part of the scientific process and it is important to understand it to understand the replication crisis. The gold standard of scientific research is to publish in peer-reviewed publications which vary in their level of prestige. The more publications in prestigious journals the more one rises trough the ranks of academia and receives more funding.

The issue is that peer reviewed journals are privately owned, even though they contain research paid for by the taxpayer, and thus require their publications to be marketable and sellable. They thus have a strong incentive to publish novel, positive results that will get people talking. This creates an incentive for researchers to produce only positive findings and over-hype their results to get published, which results in scientific journals containing a lot of false positives.

Moreover, peer review seems to be a terrible mechanism to filter research by quality. Different NeurIPS reviewers, the most prestigious machine learning conference, disagree with one another so often that it starts to resemble random chance.

These issues contribute to the replication crisis and make it hard to know which papers in the literature are reliable.

Benchmark hacking

One of the main criticisms drawn at machine learning research is its focus on getting better performances on benchmark datasets with new algorithms and its neglect of real world problems. This issue seems to come from scientific journals. They are the ones who privilege papers with novel techniques that showcase improvement on benchmark datasets, even if marginal, over practical problem-solving with machine learning.

A large part of the scientific community seems to think that new algorithms are more important than applying the algorithms we already have to new problems. Their rationale might be that once an algorithm exists applying it to real world problem is just a matter of execution and does not require further creative work. This vision is wrong however, to quote the MIT technology review piece :

One reason applications research is minimized might be that others in machine learning think this work consists of simply applying methods that already exist. In reality, though, adapting machine-learning tools to specific real-world problems takes significant algorithmic and engineering work.

Benchmark datasets tend to be unrepresentative of datasets used in real world problem solving. They are much more likely to be large, curated and to have clear cut categories. Knowing this, it is natural to suspect the methods that have been successful on benchmark data to fail on new data, especially if they are qualitatively different. Some people have begun referring to this phenomenon as benchmark hacking, in reference to p-hacking in statistics, because in both cases the findings don’t hold on new data.

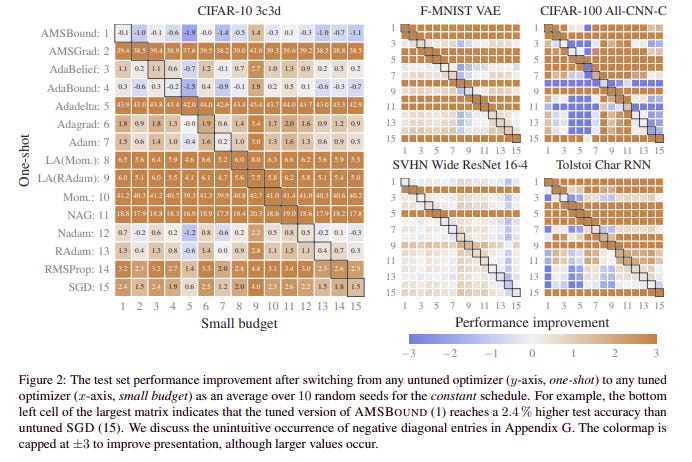
Schmidt et al. provide empirical evidence for this by comparing 15 different neural network optimizers and their results are presented in the table below :

Rows represent the untuned version of the 15 models and columns represent the same models but with a small tuning budget. A mostly orange row means that the untuned version of the optimizer is incapable of beating the tuned version of competitors, a mostly blue line means the contrary. As we can see, on all 5 datasets there is an optimizer that outperforms or equals the tuned version of the others as shown by blue or white rows.

Note that these algorithms were accepted for publication by claiming they made significant improvements, but it turns out most of them could be beaten by the untuned version of several competitors on the 5 five datasets. It also happens that most new algorithms (in their un-tuned version) can be beaten by stochastic gradient descent, or other already existing algorithms, with a small tuning budget.

Nonetheless, this could be a crucial finding for practitioners, whose resources are limited. Trying several optimizers without tuning them and then choosing the best can lead to competitive performance while saving time. Also, systematically using stochastic gradient descent and spending a little bit of time tuning it can lead to competitive results without having to overthink what optimizer to choose.

Recommender systems replication attempt

Ferrari Dacrema et al. provide us with further evidence of the replication crisis in machine learning. They attempt to reproduce the results of 18 papers using deep learning published in the recommender systems literature. They find that they are only able to reproduce 7 out of 18 of the papers with reasonable effort while 6 of them can be beaten by benchmarks such as a KNN… Even though the sample is pretty small, this is pretty terrible news. If the rate of solid, reproducible of papers in the literature rate were 90%, what would be the likelihood of drawing 18 from that population and almost all of them being either impossible to reproduce or useless as they can be easily beaten ?

Kapoor et al. replication attempt in applied ML

Kapoor et al. are currently working on a reproducibility study of applied machine learning research. Helpfully, they made their preliminary findings available on their website at Princeton. Here is what they found so far :

As you can probably see, this is pretty depressing. In some branches of applied ML like computer security and radiology, all tested papers had flaws ! The most common errors seem to be nothing foreign, they’re mostly forms of data leakage, the stuff we’re warned about in machine learning 101. It is however true that data leakage can happen in insidious ways and is not always obvious. Also, these are papers in other scientific fields that implement machine learning, some of these papers might have been written exclusively by scientists from other fields with little experience in machine learning.

But it seems that Genevera Allen, who we mentioned earlier, was right. Machine learning, which can be much more powerful than standard regression analysis traditionally used in research, might be facilitating overfitting in other scientific fields ! As if questionable research practices weren’t common enough as it was.

Is it possible to estimate the replication rate in ML ?

It depends what standard we use for replication. If we mean the percentage of papers papers which propose a new machine learning method that beats its competitors on many different datasets, then I’m afraid the figure is likely to be disappointingly low… In our first piece of evidence, none of the new optimizers was able to consistently beat its untuned competitors. The sample was small (n=15) but the fact that none of them succeed at that task does bear important signal. If I had to guess, my rough estimate would be between 1-10 %.

But note that a tremendous amount of machine learning papers are produced every year, so even if the proportion of novel, generalizable findings is low, that would still mean that the absolute number of papers which meet this criterion is significant. The issue is not so much that good work is not being done, it is more that the good work is lost in an ocean of false positives. My humble opinion would be that the solution lies in curating the literature a little better by reforming or replacing peer review so that the incentive structure ceases to be so messed up.

Now for applied ML, what is the percentage of papers that actually advance the state of the art on a given problem, either by improving the prediction accuracy or by making prediction cheaper and faster (by not requring an expert anymore for example) ? I would say it’s higher, but still pretty low. If we gather the data from Kapoor et al. for all research fields where they have finished reviewing the papers, ~62% of them were not found to have flaws. However, even without flaws their proposed protocols might be of little value if they cannot equal or approach expert performance in the field or beat pre-existing benchmarks like linear regression or KNN. Therefore, I would speculate that the percentage of papers in applied ML which truly create value is in the 25-35 % range.

These are my guesses after having reviewed the literature on the replication crisis in machine learning. Please do not take these figures at face value, only use them are heuristics to stay skeptical when reading research papers which make bold claims of SOTA performance. The only way to truly know the replication rate of machine learning research would be trough a large scale replication project. I am hopefully that one will be undertaken in the future, and only then will we be able to judge my predictions.

Final thoughts

Machine learning suffers from the strong hype around it, and in hyped research fields replicability and reproducibility tend to suffer. In cancer research, it is estimated that only 11% of new drug trials are replicable.

It is important to stay hopeful and optimistic, as one would never think to defund cancer research because of it’s low replication rate. In fact, perfect replicability is neither possible nor desirable. The scientific method itself suffers from the base rate problem. Most hypotheses we are going to test before finding a solution are going to be false, it is therefore normal to experience false positives. We might produce mostly false positives until we find a drug that actually cures cancer for good. False positives are the price to pay when the reward is large.

In fact, as we’ve said earlier, the replication crisis is not a crisis. It is not acute, but chronic. It is how science has worked for a long time. That does not mean we should not or cannot improve it. In fact, doing so might be one of the highest return on investment things one can do, from a utilitarian perspective. Weeding out false positives from the literature would save millions of dollars from being wasted on methods that don’t work and would accelerate scientific progress which is inseparable from human welfare. And even though machine learning suffers from a replication crisis, it might itself be the solution to this crisis.

What we know about machine learning’s replication crisis