Link to arxiv preprint: Do language models plan for future tokens, by Wilson Wu, John X Morris and Lionel Levine.

TLDR

There are two reasons why the computations for the current token are helpful for future tokens’ computation. First, which they call ‘pre-caching’, the network is intentionally helping future tokens’ computations by sacrificing performance for the current token. Second, which they call ‘breadcrumbs’, is that the helpfulness is incidental: the computations that are good for the current token are also good for future tokens.
By zeroing appropriate gradients, they create a training strategy that prevents pre-caching. They call this ‘myopic descent’.
On a synthetic dataset designed for pre-caching to be useful, they find strong evidence that myopic descent reduces pre-caching.
On integer multiplication, myopic descent reduces performance.
On a language dataset, they train a GPT-2 transformer using both vanilla training and myopic descent and find that performance is similar, suggesting that breadcrumbs are more prominent.
Using larger models from the Pythia suite, they find the performance gap between vanilla and myopic training increases with model size.

As of 27 June 2024, this is ongoing work. In particular, the integer multiplication and Pythia experiments are not yet described in the current arXiv article. The authors shared a draft containing these latest results.

Also, this is my first distillation post. Any feedback—both what you like and what can be improved—will be much appreciated.

Pre-requisites

For this distillation, I assume basic familiarity with transformer architecture and gradient descent. You do not need any AI safety or mech interp experience.

Pre-caching and breadcrumbs

With the help of the diagram below, I introduce notation. $x_{1}, x_{i}, x_{j}$ (where $i < j$ ) represent input tokens, $y_{1}, y_{i}, y_{j}$ represent output logits, each box corresponds to one position/token of the input sequence, and the $x$ ’s inside the boxes represent the hidden states.

We have a causal mask, so the hidden states for $x_{i}$ are useful for the hidden states for $x_{j}$ but not vice versa. The question this paper asks whether this usefulness is intentional or incidental? They introduce terminology for these two possibilities:

Pre-caching. Some computations done for $x_{i}$ are directly intended to help in future tokens, even if those computations do not help calculate $y_{i}$ .
Breadcrumbs. If computations in $x_{i}$ are helpful for future tokens, it is incidental. It just so happens that the computations necessary to calculate $y_{i}$ are also useful for predicting $y_{j}$ .

Myopic descent

To determine how much pre-caching and breadcrumbs there is, they introduce a training scheme in which pre-caching is impossible, by zeroing the parts of the gradients that incentivize pre-caching. (By gradients here I mean the gradient of the loss w.r.t. the parameters theta.) They call this ‘myopic descent’, because it is short-sighted.

The main idea is to break up the gradient into a sum of sub-gradients, grad[i,j], where grad[i,j] tells you how much the loss due to $y_{j}$ changes if you make a small change to theta, BUT, the change to theta is only done for $x_{i}$ ’s hidden states, not any of the other tokens.

*Red indicates those items that change as a result of changing theta in only the i-th position.*

More explicitly, imagine doing a forward pass in which we replace theta with $θ + δ θ$ only for the hidden states of the $i$ -th position: we leave $θ$ unchanged for all other sequence positions. Because of the causal architecture, only the hidden states and outputs from the $i$ -th position onwards will be impacted.grad[i,j] is the change in the loss from $y_{j}$ by doing this small change to theta in position $i$ .

grad[j,i] is always zero, because hidden states for $x_{j}$ have no impact on $y_{i}$ .
The diagonal gradients grad[i,i] teach the transformer to better predict $y_{i}$ from $x_{i}$ , i.e. directly predicting the next token.
The off-diagonal gradients grad[i,j] teach the transformer to better predict $y_{j}$ from $x_{i}$ , i.e. helping predict future tokens. It is these gradients that result in pre-caching so it is these gradients that are zeroed!

Synthetic dataset experiment

They create a synthetic numerical dataset in which pre-caching is obviously useful. For simplicity, I present a special case of the data generating process:

The input tokens $x_{1}, . . ., x_{N}$ are i.i.d standard normal, so $x_{n} \sim N (0, 1)$ .
The output tokens $y_{1}, . ., y_{N}$ are defined as $y_{n} = x_{n} + \sum_{i = 1}^{10} sin (x_{n - i})$ , so the sum of the current $x$ with the sum of the sine of the previous 10 $x$ ’s.

The idea is that calculating $sin (x_{i})$ is not useful for calculating $y_{i}$ , but it is useful for the next 10 $y$ ’s. Hence, if we saw the transformer calculating $sin (x_{i})$ in the $i$ -th position, that means the transformer is pre-caching.

They train two transformers (with GPT2 architecture) on 30,000,000 sequences created from this process, one with vanilla training and the other with myopic descent. By doing simple investigations into the neurons (calculating correlations and using linear probes), they find strong evidence that the vanilla transformer was doing pre-caching and the myopic transformer was not. See Figures 2, 3 and 4 in the paper.

Integer multiplication experiment

They train two transformers (with GPT2 architecture) to do integer multiplication, one vanilla and one myopic. They use several tricks from Shen et al. (2023) to improve performance:

Characters are delimited by spaces, so each digit becomes one token.
All numbers are written in the reverse of the standard order, so the least significant digits come first.
All inputs are zero-padded to the same length and the output is padded to twice that length.

Hence, an example looks like:

3 7 0 0 * 5 4 0 0 = 5 8 2 3 0 0 0 0

Both the vanilla and myopic model are trained for one epoch on 10,000,000 examples, with at most 8 digits for each multiplicands. We see from the accuracy scores below that vanilla training performs better.

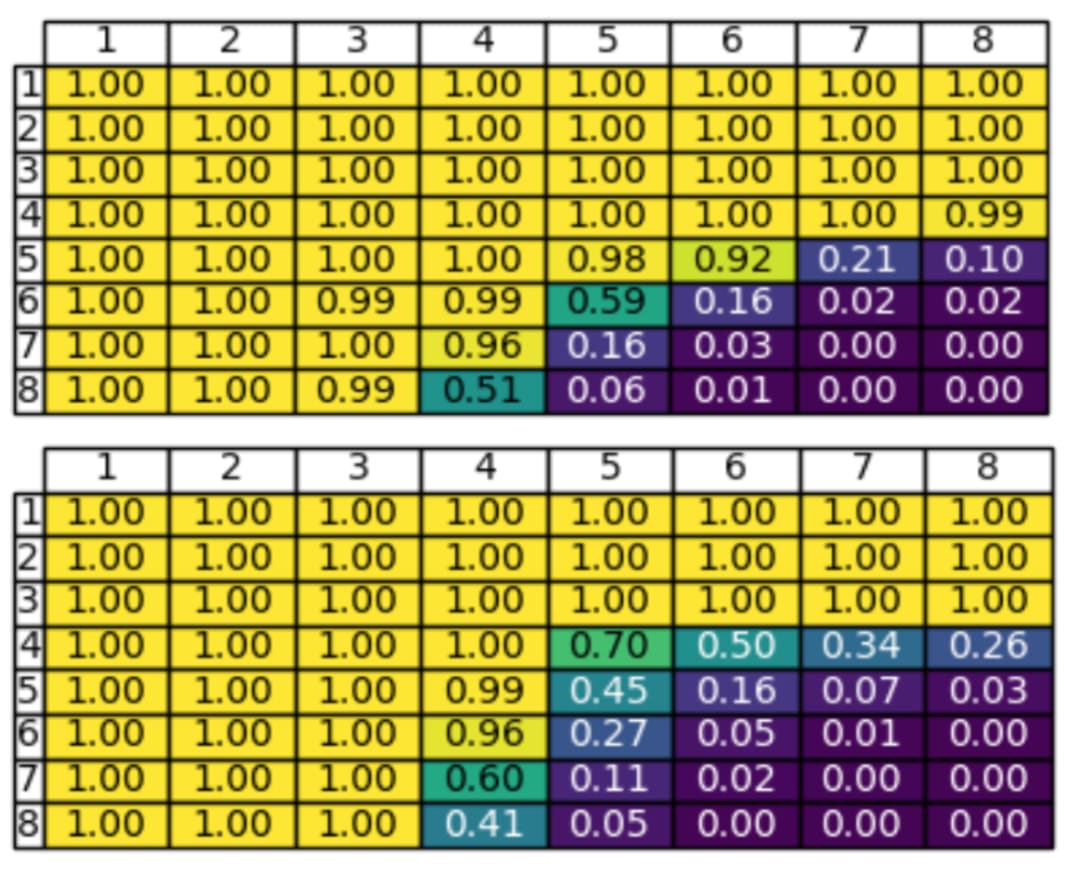
*The first table is for vanilla training. The second for myopic descent. The row and column number indicate the number of digits in the two numbers being multiplied.*

The authors hypothesize that the vanilla transformer can make use of filler tokens, as in Pfau et al (2024) where it was found that adding ellipsis ‘...’ improves performance. To test this hypothesis, they train vanilla and myopic transformers on each of two different datasets:

both numbers being multiplied have at most 5 digits and are zero-padded to 5 digits
both numbers being multiplied have at most 5 digits but are zero-padded to 10 digits.

Looking at the accuracy scores below, we see that the vanilla transformer benefits from the padding whereas the myopic transformer suffers.

Quoting the authors:

We hypothesize that the increased input length makes it more difficult for the attention mechanism [for the myopic model] to correctly attend to the relevant tokens.

GPT2 language experiment

I quote the paper (with redactions):

All models use the 124M-parameter GPT-2 architecture. We train all models (vanilla and myopic) from random initialization for one epoch on 4.6M sequences from the MS MARCO dataset (Nguyen et al., 2016), truncated to length 64. As a baseline, we also train a “transformer bigram” model, a model with an identical architecture but all off-diagonal key/value states zeroed out.

The cross entropy on a validation set for these three models is:

Vanilla 3.28
Myopic 3.40
Transformer bigram 5.33

We see that the vanilla model does have a better score than the myopic model, but not large compared to naive bigram baseline. This suggests that pre-caching does provide some benefit but breadcrumbs are doing most of the work.

We get a more refined view of what is happening when we compute the loss on a per-position basis.

*‘Myopia gap’ is the difference in loss between the myopic and vanilla models, so the green curve on the right is just the difference between the orange and blue curves on the left.*

Again, just quoting the authors:

We see that the myopic model outperforms the vanilla model at the beginning of the sequence, but falls behind as the length of the past increases. This implies that a lack of pre-caching may compound, and model performance degrades later in the sequence as the model is unable to refer to prior pre-cached information.

Pythia language experiments

What happens when we scale the experiments? Details of the training:

We train both vanilla and myopic transformers from the Pythia LLM suite (Biderman et al., 2023), ranging in size from 14M to 2.8B parameters, on one epoch of 10M examples subsampled from the Pile dataset (Gao et al., 2020). (Note that this is the same subsampled dataset for every training model.) Note that, unlike in the GPT2-small experiments which start from random initialization, we start all training for Pythia models from the pre-trained checkpoints provided by Biderman et al. (2023). The 10M-example dataset we use is not sufficiently large to train from random initialization.

The results show that the gap in performance increases as you increase the model size. First, this is seen in the cross entropy loss:

Similar patterns are seen in the performance of the models on various benchmarks. Here are two examples:

A question from a reviewer

One of the reviewers of this post, Julian, asked whether the myopic model is disadvantaged by being trained with the same number of epochs / samples as the vanilla model. An author answered with:

It’s not clear how to quantify this [potential disadvantage], so training the vanilla and myopic models for the same number of steps is the fairest we could come up with. In any case, this disparity should (intuitively) only disadvantage the myopic model. Thus, it only strengthens our position that in GPT-2 there is little pre-caching occurring.

I asked a follow-up about what would happen if the the myopic model was trained more, to see whether the gaps close. Their response:

We ran all of our experiments in an “infinite data” setting (single epoch over a large train dataset) in order to disentangle the effects we’re investigating from phenomena related to small datasets, overfitting, grokking, etc.
The number of training steps we used for the toy example (30,000,000) was enough that the vanilla model flatlined at zero for most of the training. Meanwhile, the myopic model was flat at the initial loss for the entire training run, so it seems unlikely that even more training would cause it to suddenly drop. (Though, of course, this can’t be ruled out for certain.)

Why read the pre-print

To see the figures for the synthetic dataset experiment.
To see how myopic descent is defined mathematically. Useful exercise, especially if you are not used to reading precise mathematical definitions.
For full details on the experiments.
For details on another type of training. Quote: “To estimate the local myopia bonus of the vanilla model, we train another model from random initialization with the same architecture, but with past hidden states provided by the vanilla model”.
For more academic or mathematical readers, they also prove some theorems around the convergence of myopic descent.

Acknowledgements

Thanks to Nicky Pochinkov, Julian Schulz and one of the authors Wilson Wu for reviewing drafts of this post. Diagrams created on bitpaper.io

Distillation of ‘Do language models plan for future tokens’