Finding the estimate of the value of a state in RL agents
Clément Dumas, Walter Laurito, Robert Klassert, Kaarel Hänni
Epistemic Status: Initial Exploration
The following is a status update of a project started as part of the SPAR program. We explored some initial directions and there are still a lot of low-hanging fruits to pick up. We might continue to work on this project, either again as part of another SPAR iteration or with others who would be interested to work on this.
TL;DR
We adapted the Contrast Consistent Search (CCS) loss to find value-like directions in the activations of CNN-based PPO agents. While we had some success in identifying these directions at late layers of the critic network and with specific informative losses, we discovered that early layers and the policy network often contained more salient features that overshadowed the value-like information. In simple environments like Pong, it might be feasible to normalize the obvious salient features (e.g., ball position and approach). However, for more complex games, identifying and normalizing all salient features may be challenging without supervision. Our findings suggest that applying CCS to RL agents, if possible, will require careful consideration of loss design, normalization, and potentially some level of supervision to mitigate the impact of highly salient features.
Motivation
The research direction of “Searching for Search” investigates how neural networks implement search algorithms to determine actions. The goal is to identify the search process and understand the underlying objectives that drive it. By doing so, we may be able to modify the search to target new goals while maintaining the model’s capabilities. Additionally, proving the absence of search could indicate limited generalization ability, potentially reducing the likelihood of deception.
A natural first step towards finding search in models is to examine a Reinforcement Learning agent and determine if we can identify the agent’s estimate of the value of a state (or action). Typically, the value network outputs this value, while the policy network outputs an action. To output an action, we think that the policy network could probably require some internal representation of value. Therefore, based on an example from our mathematical framework, we employed both unsupervised and supervised probing methods to try to uncover the value of a state of a value network and policy network.
As one might expect, we were able to successfully identify the value of the state in the value network with the unsupervised method. However, in the case of the policy network, we are only able to identify the representation of the values of a state in a supervised way. This document provides an overview of our current progress.
Method
We trained PPO agents to play the pong game in a multiagent setting[1]. However, it seems that the model struggles to accurately estimate the value of a state, as it predicted mostly even values until the ball passed the agent, as seen in the video below.
Low-hanging fruit 🍉: It would be interesting to try other games in which the agent can have a better estimate of the value of its state throughout the game.
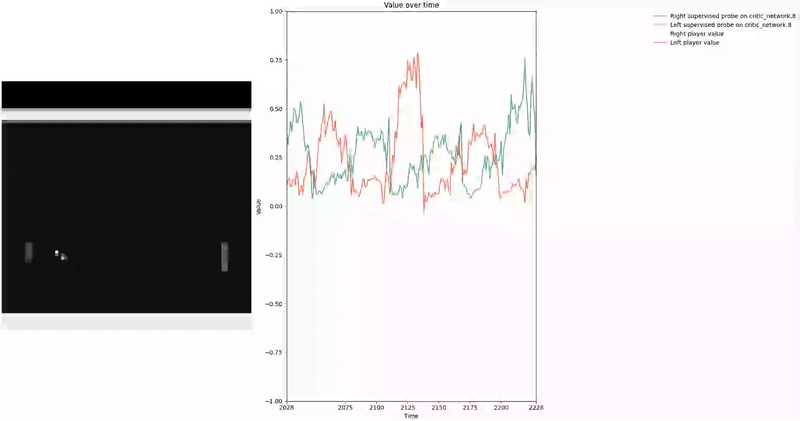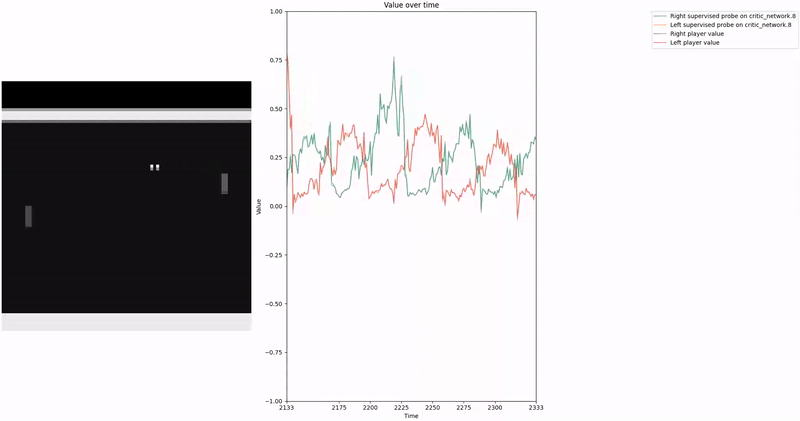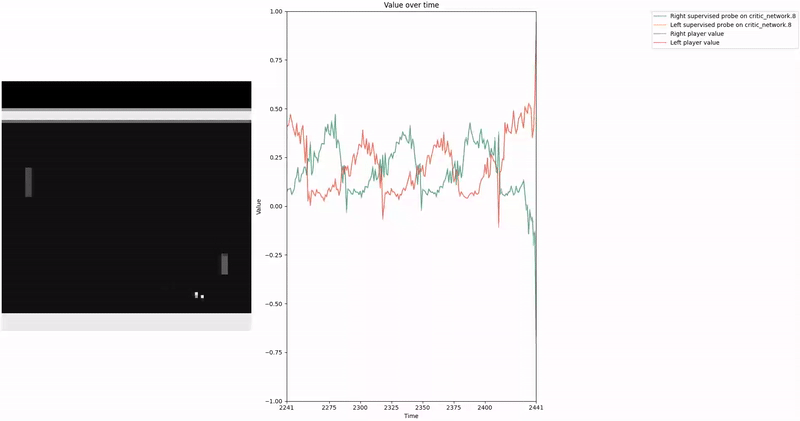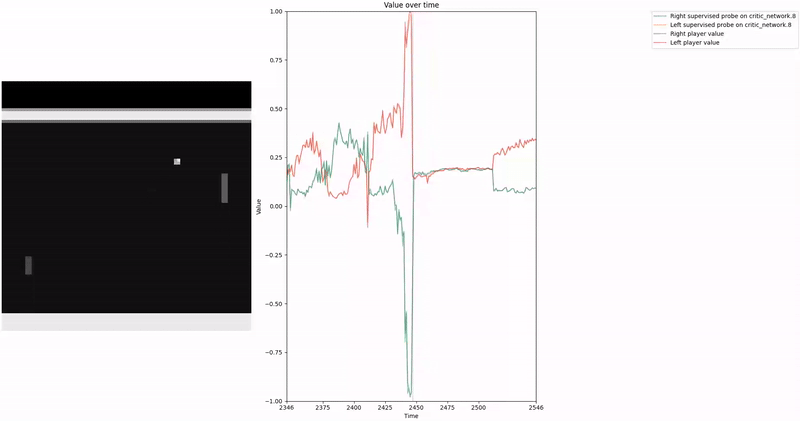
Our agent zoo contains agents trained with a shared CNN for the value and policy head, as well as agents trained with separate CNNs for each head. We mostly studied the multi_agent_train_fixed/ppo_multiagent_2.cleanrl_model model as it was the most capable one with separate CNNs.
Low-hanging fruit 🍎: we ended up not inspecting our shared CNN agents
Given hidden activations of a policy and value network of a PPO agent, we trained both unsupervised and supervised probes with the aim of being able to output the represented value of a state within the network.
Low-hanging fruit 🍋: we didn’t compute any quantitative measure of our probes relative to the ground truth discounted reward / the agent value
Unsupervised Probing
Unsupervised probing aims to identify concepts within models. Its main strength is that it achieves this without relying on labeled data, making it a powerful tool for understanding the internal representations learned by the model.
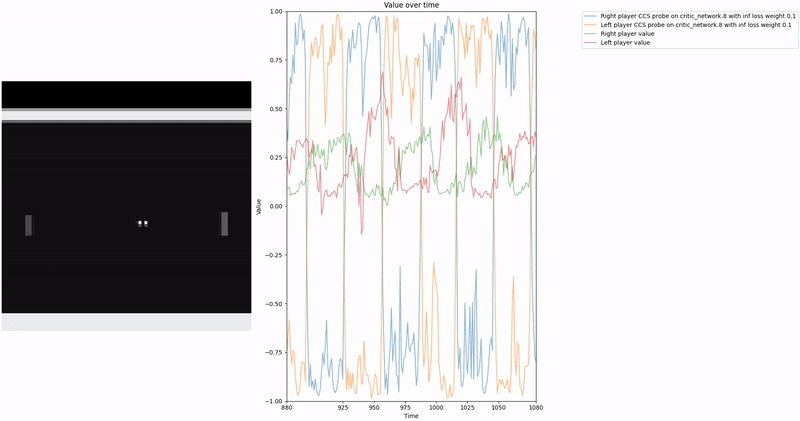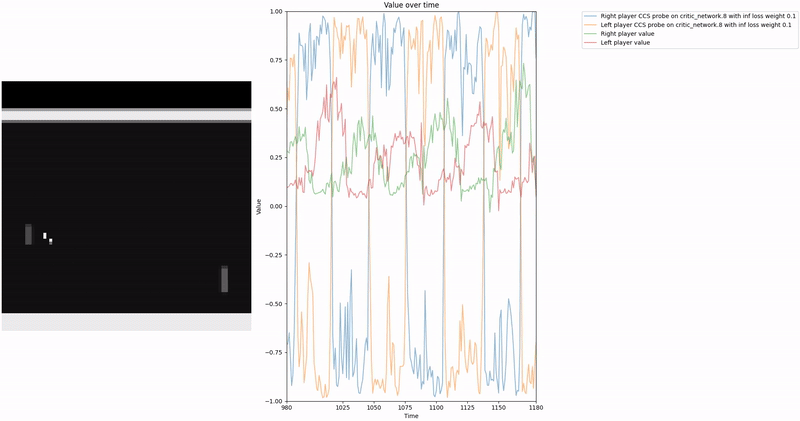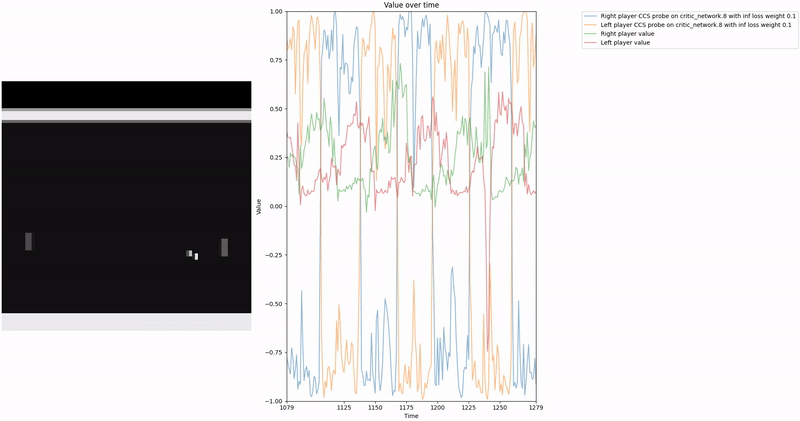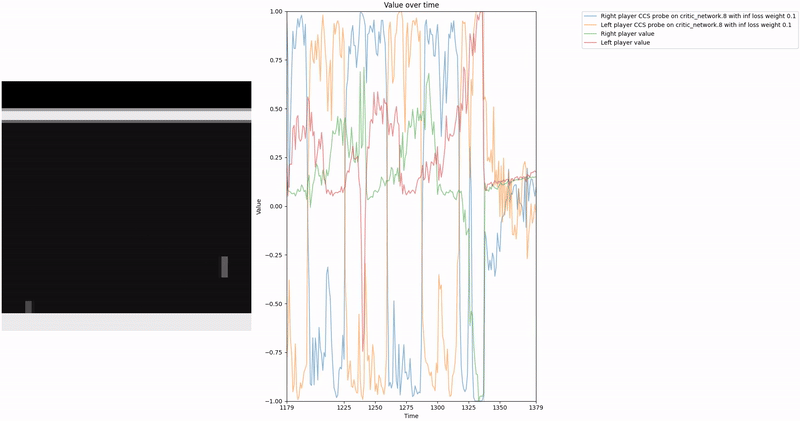
Based on our previous work, we constructed a loss function to train a probe using Contrast Consistent Search (CCS). Since CCS requires a set of contrast pairs, a straightforward approach to generate these pairs in the context of two-player games, such as Pong or Bomberman, is to consider the game state from the perspectives of both players.
Low-hanging fruit🍐: CCS is not the only unsupervised method which uses contrast pairs it would be interesting to look at those too.
We aim for our CCS probe to find values within the range . In a two-player zero-sum game, at any given time, if player1 assigns a value to a state , then the value for the corresponding state from player2′s perspective should be , as player2′s gain is player1′s loss. We leverage this symmetric relationship between the players’ values to construct our consistency loss, which encourages the probe to find value-like directions that satisfy this property.
In addition, similar to CCS, we add an informative term to the loss to avoid the trivial solution of assigning 0 to and :
By combining them and adding a weight to the informative loss, we obtain the loss function:
To train the probe, we first create a dataset of contrast pair by letting 2 agents play against each other and collecting their perspectives at each time step. We then pass all the pairs through the network to collect activations at a given layer and train the probes on those activation contrast pairs.
Supervised Probing
We also train supervised probes on each layer as a baseline, where we used the outputs of the value head for each observation as labels.
Experiments and Results
Value Head CNN Experiment
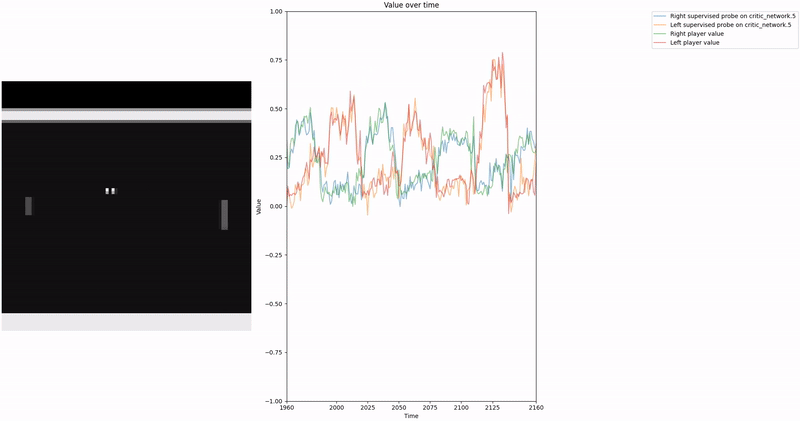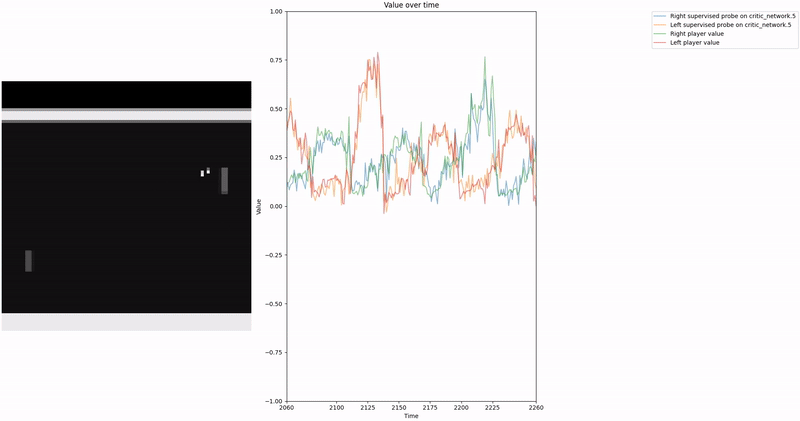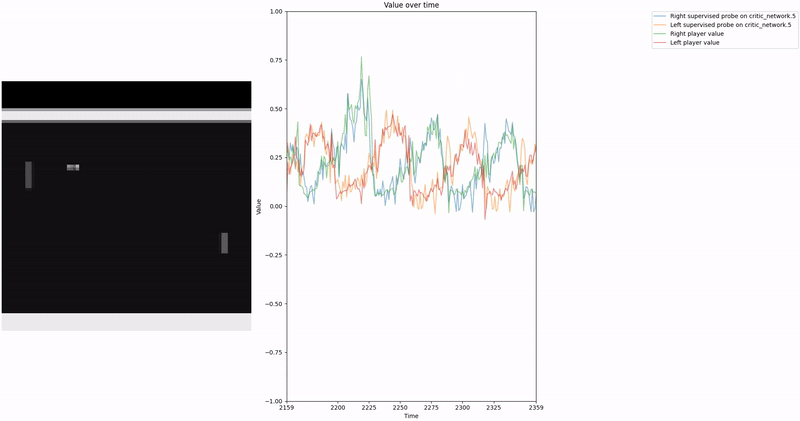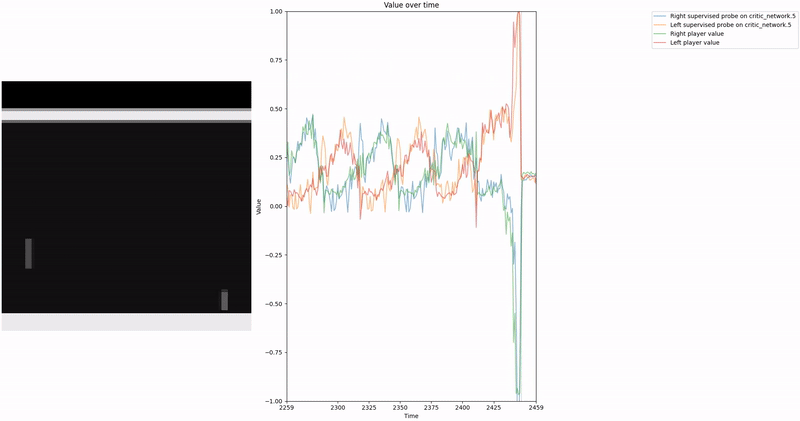
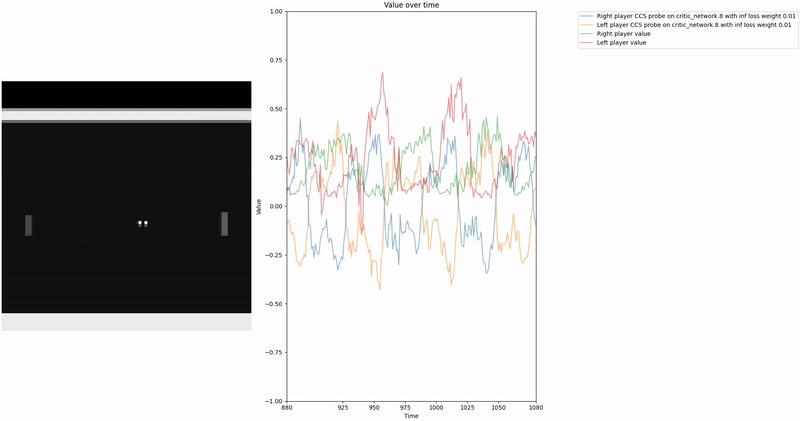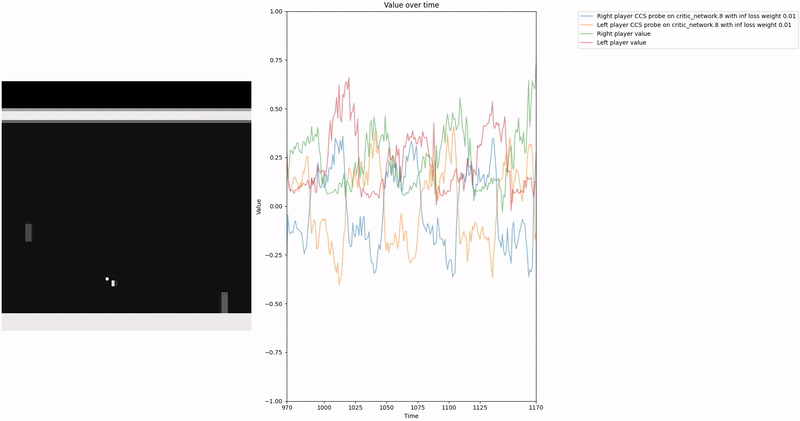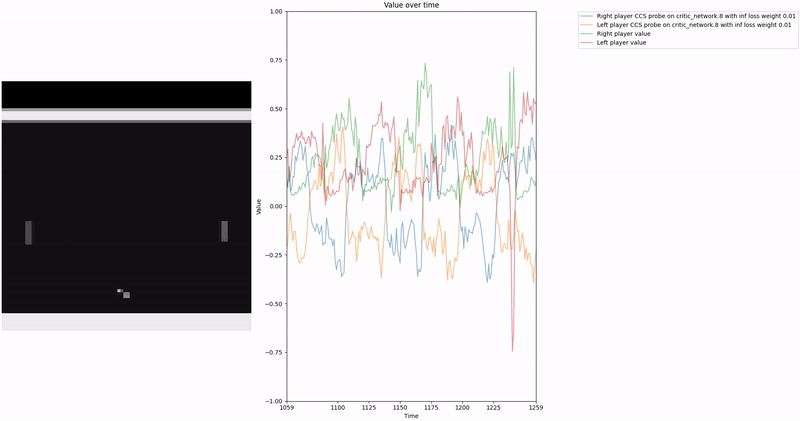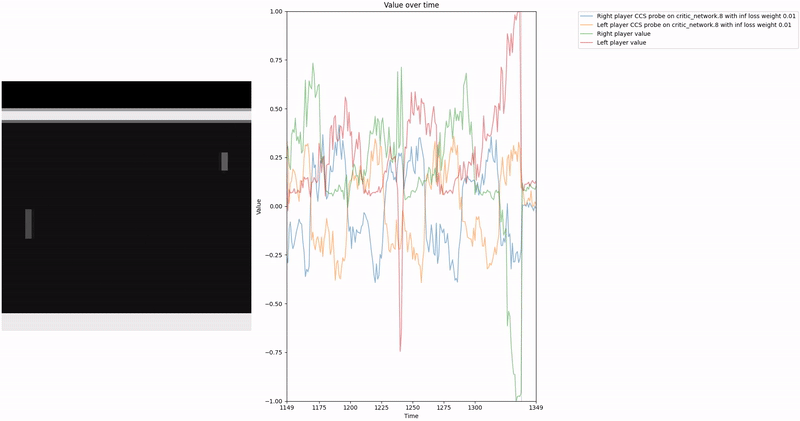
Policy Head Experiment
Unsupervised vs Supervised
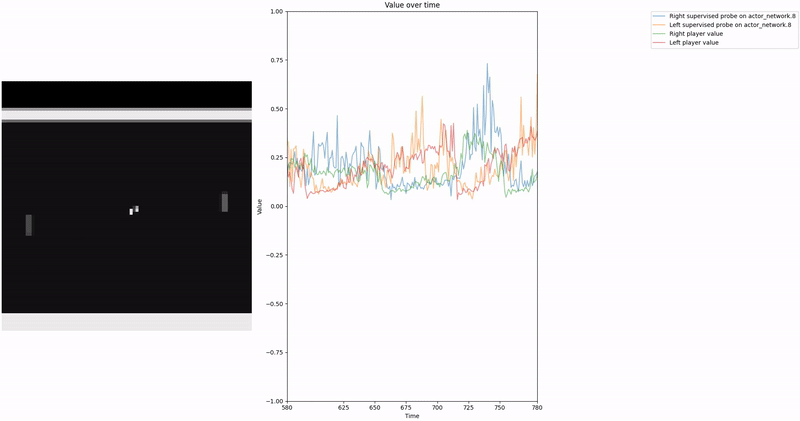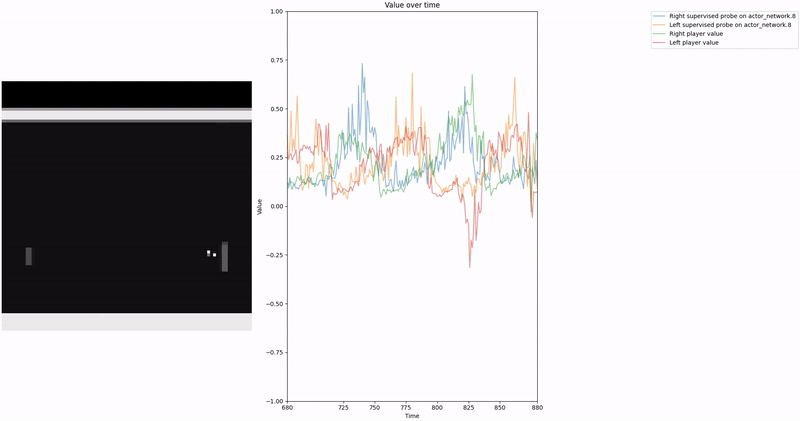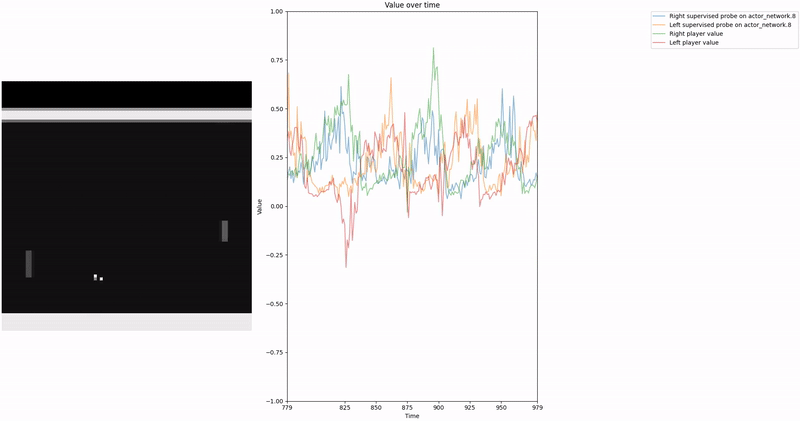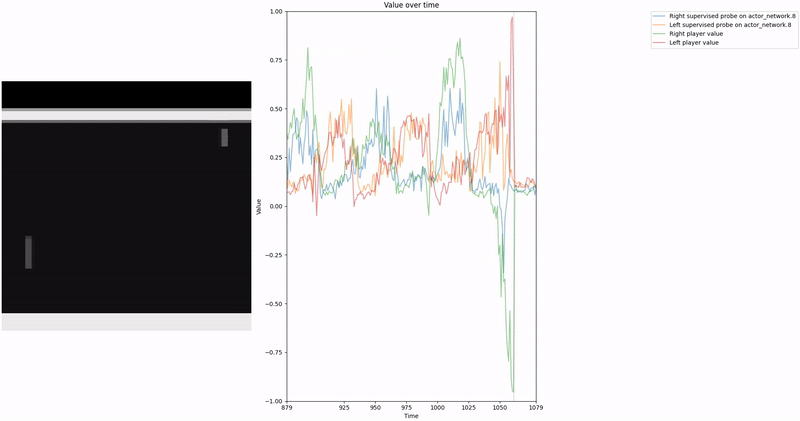
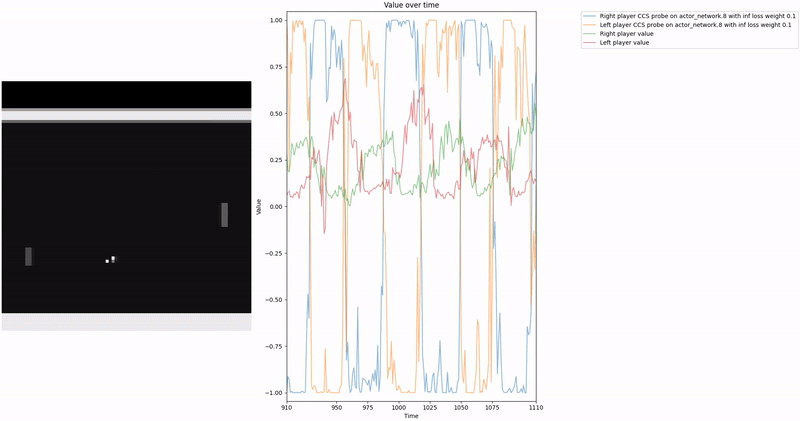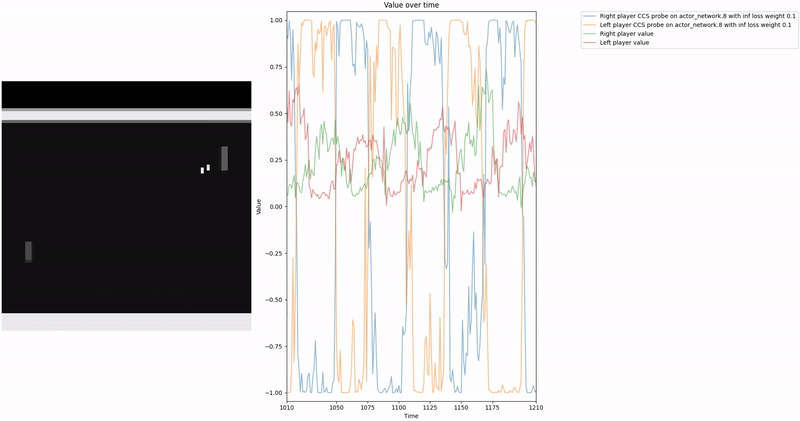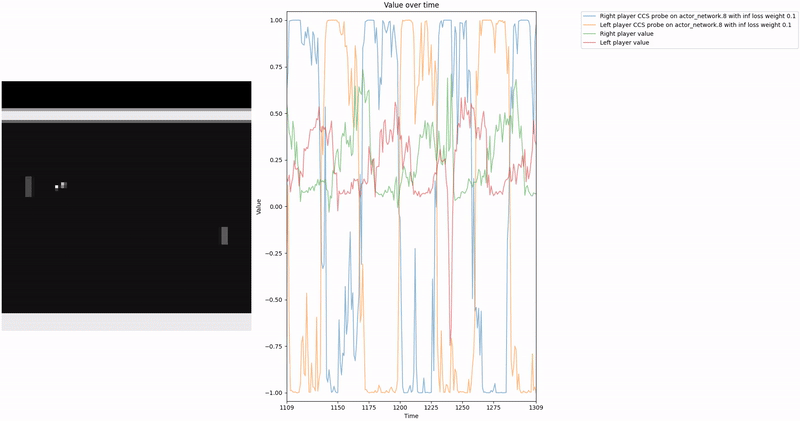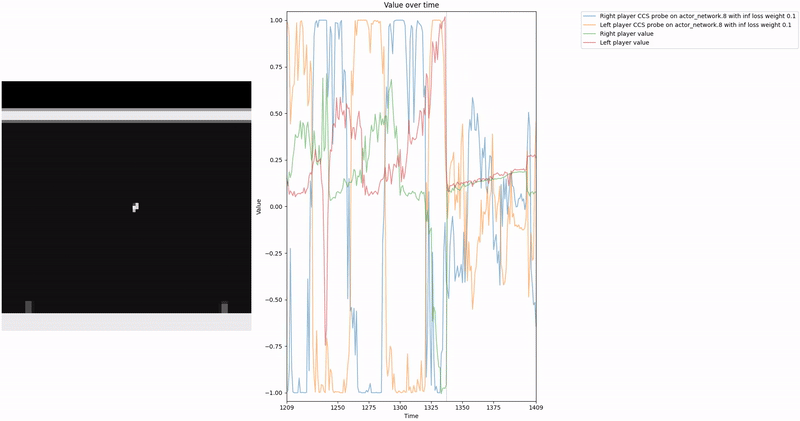
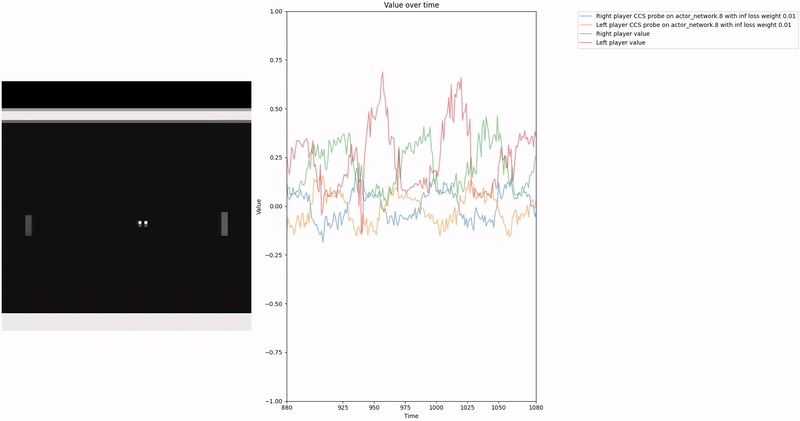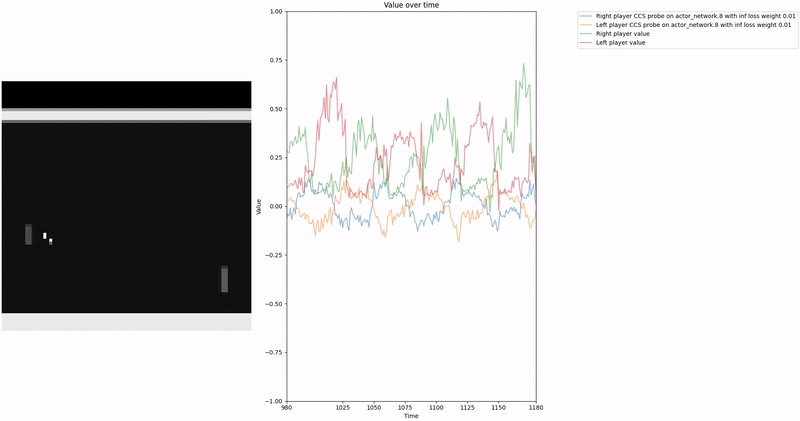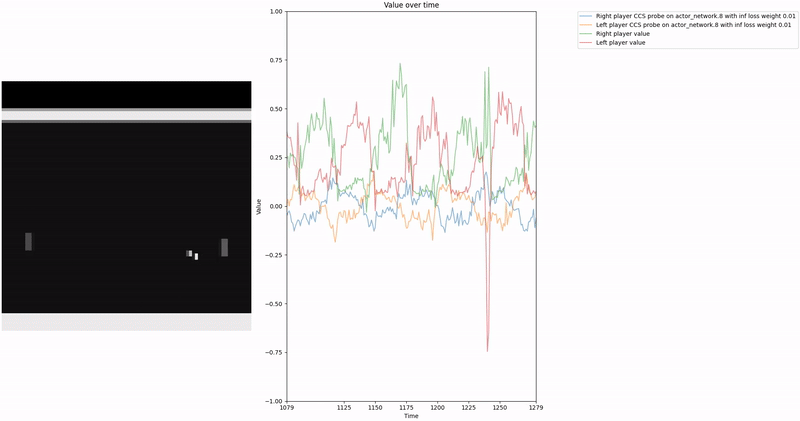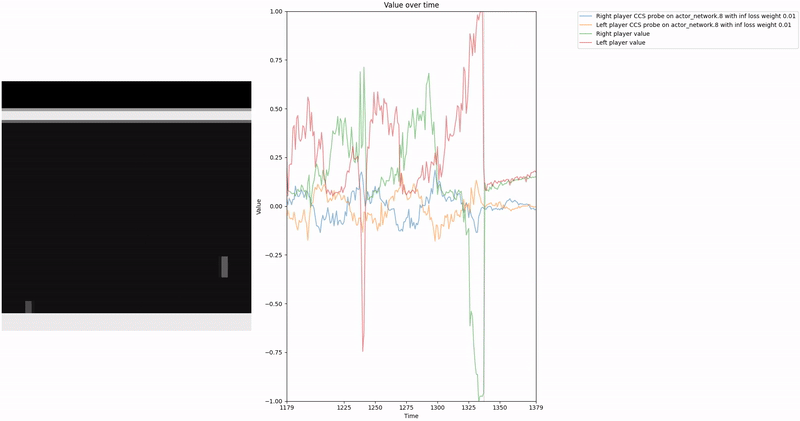
As demonstrated in the visualizations, our CCS probe identifies two key features in certain layers of the model instead of a value feature: “which side the ball is on” and “which side the ball is approaching.” This suggests that the model may not be learning a true value function, but rather focusing on these more superficial features of the game state. Changing the value of the information loss weight didn’t help much.
We attempted to apply normalization techniques as described in the CCS paper, where they normalize all prompts ending with “yes” or “no” to prevent the probe from exploiting those directions. However, our implementation of this normalization was never thoroughly tested.
Low-hanging fruit 🥭: Properly implement and test the normalization techniques for removing those two features to determine if they lead to a better CCS probe that is more likely to identify value-like features rather than superficial game state features.
Related work
Searching for a model’s concepts by their shape – a theoretical framework
Discovering Latent Knowledge
https://arxiv.org/abs/2212.03827
High Level interpretability
Searching for Searching for Search
https://www.lesswrong.com/posts/b9XdMT7o54p5S4vn7/searching-for-searching-for-search
Searching for Search
https://www.lesswrong.com/posts/FDjTgDcGPc7B98AES/searching-for-search-4
Maze Solving Policy Network
Pretty interesting! Since the world of pong isn’t very rich, would have been nice to see artificial data (e.g. move the paddle to miss the ball by an increasing amount) to see if things generalize like expected reward. Also I found the gifs a little hard to follow, might have been nice to see stills (maybe annotated with “paddle misses the ball here” or whatever).
If the policy network is representing a loss function internally, wouldn’t you expect it to actually be in the middle, rather than in the last layer?
In the course of this project, have you thought of any clever ideas for searching for search/value-features that would also work for single-player or nonzero-sum games?
Thanks for your comment! Re: artificial data, agreed that would be a good addition.
Sorry for the gifs maybe I should have embedded YouTube videos instead
Re: middle layer, We actually probed on the middle layers but the “which side the ball is / which side the ball is approaching” features are really salient here.
Re: single player, Yes Robert had some thought about it but the multiplayer setting ended up lasting until the end of the SPAR cohort. I’ll send his notes in an extra comment.
We are given a near-optimal policy trained on a MDP. We start with simple gridworlds and scale up to complex ones like Breakout. For evaluation using a learned value function we will consider actor-critic agents, like the ones trained by PPO. Our goal is to find activations within the policy network that predict the true value accurately. The following steps are described in terms of the state-value function, but could be analogously performed for predicting q-values. Note, that this problem is very similar to offline reinforcement learning with pretraining, and could thus benefit from the related literature.
To start we sample multiple dataset of trajectories (incl. rewards) by letting the policy and m noisy versions thereof interact with the environment.
Compute activations for each state in the trajectories.
Normalise and project respective activations to m+1 value estimates, of the policy and its noisy versions: vθi(~ϕ)=tanh(θTi~ϕi+bi) with ~ϕ(s)=ϕ(s)−μσ
Calculate a consistency loss to be minimised with some of the following terms
Mean squared TD error La(θ)∝∑Nn=1∑Tnt=1[vθ(~ϕ(snt))−(Rnt+1[t<Tn]γvθ(~ϕ(snt+1)))]2
This term enforces consistency with the Bellman expectation equation. However, in addition to the value function it depends on the use of true reward “labels”.
Mean squared error of probe values with trajectory returnsLb(θ)∝∑Nn=1∑Tnt=1[vθ(~ϕ(snt))−Gnt]2
This term enforces the definition of the value function, namely it being the expected cumulative reward of the (partial) trajectory. Using this term might be more stable than (a) since it avoids the recurrence relation.
Negative variance of probe values Lc(θ)∝−∑Nn=1∑Tnt=1[vθ(~ϕ(snt))−¯vθ]2
This term can help to avoid degenerate loss minimizers, e.g. in the case of sparse rewards.
Enforce inequalities between different policy values using learned slack variables Ld(θ,θi,λi)∝∑s∑i∈{1,m}(vθ(s)−vθi(s)−σλi(s)2)2
This term ensures that the policy consistently dominates its noisy versions and is completely unsupervised.
Train the linear probes using the training trajectories
Evaluate on held out test trajectories by comparing the value function to the actual returns. If the action space is simple enough, use the value function to plan in the environment and compare resulting behaviour to that of the policy.
Thanks for the reply! I feel like a loss term that uses the ground truth reward is “cheating.” Maybe one could get information from how a feature impacts behavior—but in this case it’s difficult to disentangle what actually happens from what the agent “thought” would happen. Although maybe it’s inevitable that to model what a system wants, you also have to model what it believes.